
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Последовательность решения задач о равновесии
Рекомендуется придерживаться следующей последовательности решения задач. 1 Выделить точку или тело, равновесие которого рассматривается. Нарисовать его отдельно. Указать все необходимые размеры. 2 Освободить тело от связей, заменив их действие реакциями. Показать на рисунке все действующие активные силы и реакции связей ( в том числе и пары сил). 3 Классифицировать эту систему сил (сходящаяся, плоская или пространственная система сил). 4 Выбрать систему координат и составить уравнения равновесия, из решения которых определить искомые величины. 5 Проверочные расчеты. В задачах о равновесии проверочные расчеты связаны с составлением лишнего (в смысле определения искомых величин) уравнения равновесия. Если задача решена верно, то это уравнение выполняется со знаком тождества. Поскольку расчеты приближенные и тождество должно выполняться в пределах принятой точности.
2.10 Контрольные задания Порядок выполнения работ Количество и номера задач в контрольной работе определяются преподавателем. К каждой задаче дается 10 рисунков и таблица (с тем же номером, что и задача), содержащая дополнительные к тексту задачи условия. Нумерация рисунков двойная, при этом номером рисунка является цифра, стоящая после точки. Например, рис. С1.4 – это рис. 4 к задаче С1 и т.д. (в тексте задачи при повторных ссылках на рисунок пишется просто рис. 4 и т.д.). Номера условий от 0 до 9 проставлены в1-м столбце (или в 1-й строке) таблицы. Во всех задачах номер рисунка выбирается по предпоследней цифре шифра, а номер условия в таблице – по последней; например, если цифр оканчивается числом 35, то берет рис. 3 и условия №5 из таблицы. Каждое задание выполняется в отдельной тетради (ученической), страницы которой нумеруются. На обложке указываются: название дисциплины, номер работы, фамилия и инициалы студента, учебный шифр, специальность. На первой странице тетради записываются: номер работы, номера решаемых задач. Решение каждой задачи обязательно начинать на развороте тетради (на четной странице, начиная со второй, иначе работу трудно проверять). Сверху указывается номер задачи, далее делается чертеж (можно карандашом) и записывается, что в задаче дано и что требуется определить (текст задачи не переписывать). Чертеж выполняется с учетом условий решаемого варианта задачи; на нем все углы, действующие силы, число тел и их расположение на чертеже должны соответствовать этим условиям. В результате в целом ряде задач чертеж получится более простой, чем общий. Чертеж должен быть аккуратным и наглядным, а его размеры должны позволять ясно показать все силы или векторы скорости и ускорения и др.; показывать все эти векторы и координатные оси на чертеже, а также указывать единицы получаемых величин нужно обязательно. Решение задач необходимо сопровождать краткими пояснениями (какие формулы или теоремы применяются, откуда получаются те или иные результаты и т.п.) и подробно излагать весь ход расчетов. На каждой странице следует оставлять поля для замечаний рецензента. Работы, не отвечающие всем перечисленным требованиям, проверяться не будут и будут возвращаться для переделки. При чтении текста каждой задачи учесть следующее. Большинство рисунков дано без соблюдения масштаба. На рисунках к задачам С1 – С3 и Д1 – Д6 все линии, параллельные строкам, считаются горизонтальными, а перпендикулярные строкам – вертикальными и это в тексте задач специально не оговаривается. Также без оговорок считается, что всенити (веревки, тросы) являются нерастяжимыми и невесомыми, нити, перекинутые через блок, по блоку не скользят, катки и колеса (в кинематике и динамике) катятся по плоскостям без скольжения. Все связи, если не сделано других оговорок, считаются идеальными. Когда тела на рисунке пронумерованы, то в тексте задачи и в таблице P1, l1, r1 и т.п. означают вес или размеры тела 1; P2, l2, r2 — тела 2 и т.д. Аналогично в кинематике и динамике vB, aB обозначают скорость и ускорение точки В; VC, aC - точки С; w1, e1 – угловую скорость и угловое ускорение тела 1; w2, e2 - тела 2 и т.д. В каждой задаче подобные обозначения могут тоже специально не оговариваться. Следует также иметь в виду, что некоторые из заданных в условиях задачи величин (размеров) при решении каких-нибудь вариантов могут не понадобиться, они нужны для решения других вариантов задачи. Из всех пояснений в тексте задачи обращайте внимание только на относящиеся к вашему варианту, т.е. к номеру вашего рисунка или вашего условия в таблице. Методические указания по решению задач, входящих в контрольные задания, даются для каждой задачи после изложения ее текста под рубрикой " Указания"; затем дается пример решения аналогичной задачи. Цель примера - разъяснить ход решения, но не воспроизвести его полностью. Поэтому в ряде случаев промежуточные расчеты опускаются. Но при выполнении задания все преобразования и числовые расчеты должны быть обязательно последовательно проделаны с необходимыми пояснениями; в конце должны быть даны ответы.
Задача С1
В этой задаче исследуется равновесие плоской системы сил. Жесткая рама (рис. С1.0 - С1.9, табл. С1) закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню BB1, или к шарнирной опоре на катках; стержень прикреплен к раме и к неподвижной опоре шарнирами.



На раму действует пара сил с моментом M = 100 Нм, распределенная нагрузка с интенсивностью q = 20 Н/м и две сосредоточенные силы, значения которых, направления, и точки приложения указаны в таблице. Параметр l = 0, 5 м. Определить реакции связей в точках A и B, которые вызваны заданными нагрузками. Указания: В задаче С1 рассматривается равновесие тела под действием плоской системы сил. Необходимо учесть, что уравнения моментов будут простыми (содержать меньше неизвестных), если в качестве полюсов принять точки, где пересекаются линии действия двух или более искомых реакций. При вычислении моментов сил там, где затруднено непосредственное определение плеч, необходимо использовать теорему Вариньона, т.е. разложить, например силу
Пример С1. Жесткая рама (рис.С1) закреплена в точке A шарнирно, а в точке B прикреплена к подвижной шарнирной опоре. Действующие нагрузки и размеры указаны на рисунке.
Определить: реакции в точках A и B. Решение 1 Рассмотрим равновесие рамы. Выберем систему координат Axy и изобразим действующие на раму силы: силы
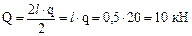 и проходит через его центр тяжести (точку пересечения медиан) на расстоянии 2/3 длины основания от вершины B: и проходит через его центр тяжести (точку пересечения медиан) на расстоянии 2/3 длины основания от вершины B: 
2 Для таким образом полученной системы сил запишем три уравнения равновесия. При вычислении моментов сил в качестве полюса выгодно выбрать точку A, так как через эту точку проходят линии действия двух искомых неизвестных сил. Плечо силы
причем Уравнения равновесия имеют вид:
Ответ: XA = 1, 35 Кн, YA = –18, 67 Кн, RB = 36, 76 Кн Проверочные расчеты. Для оценки правильности результатов составим еще одно (" лишнее" ) уравнение равновесия. В качестве полюса выгодно (уравнение получится проще) принять точку H.
18, 67× 2× 0, 5 – 80 + 20× 0, 5× 4× 0, 5 – 20× 0, 866× 2× 0, 5 + 36, 76× 0, 707× 4× 0, 5 + 6, 67 = 0, 01 » 0 Таким образом, задача решена верно. Знак (-) при YA указывает, что эта реакция направлена противоположно показанной на рис. С1.
Задача С2 В задаче рассматривается равновесие системы тел (системы сочлененных объектов). Конструкция состоит из жесткого угольника и стержня, которые в точке С или соединены друг с другом шарнирно (рис. С2.0 – С2.5), или свободно опираются друг о друга (рис. С2.6 – С2.9). Внешними связями, наложенными на конструкцию, являются в точке А или шарнир, или жесткая заделка; в точке В или гладкая плоскость (рис. 0 и 1), или невесомый стержень ВВ¢ (рис. 2 и 3), или шарнир (рис. 4 – 9); в точке D или невесомый стержень DD¢ (рис. 0, 3, 8), или шарнирная опора на катках (рис. 7). На каждую конструкцию действуют: пара сил с моментом М = 60 кН× м, равномерно распределенная нагрузка интенсивности q = 20 кН/м и еще две силы. Эти силы, их направления и точки приложения указаны в табл. С2; там же в столбце " Нагруженный участок" указано, на каком участке действует распределенная нагрузка (например, в условиях №1 на конструкцию действуют сила



Определить реакции связей в точках А, В, С (для рис. 0, 3, 7, 8 еще и в точке D), вызванные заданными нагрузками. При окончательных расчетах принять а = 0, 2 м. Направление распределенной нагрузки на различных по расположению участках указано в табл. С2а.
Пример С2. На угольник ABC (Ð ABC = 90°), конец А которого жестко заделан, в точке С опирается стержень DE (рис. С2а). Стержень имеет в точке D неподвижную шарнирную опору и к нему приложена сила Дано: F = 10 кН, M = 5 кН× м, q = 20 кН/м, a = 0, 2 м. Определить: реакции в точках А, С, D, вызванные заданными нагрузками.
 Решение Решение
1 Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня DE (рис. С2б). Проведем координатные оси ху и изобразим действующие на стержень силы: силу
å Fkx = 0, XD + F – N× sin 60° = 0 (1) å Fky = 0, YD + N× cos 60° = 0 (2)
2 Теперь рассмотрим равновесие угольника (рис. С2в). На него действуют сила давления стержня å Fkx = 0, XA + Q× cos 60° + N¢ × sin 60° = 0 (4) å Fky = 0, YA + Q× sin 60° + N¢ × cos 60° = 0 (5)
При вычислении момента силы Ответ: N = 21, 7 кН, YD = -10, 8 кН; XD = 8, 8 кН, XD = -26, 8 кН, YA = 24, 7 кН, Знаки указывают, что силы Задача С3 В этой задаче исследуется равновесие пространственной системы сил. Однородная прямоугольная плита весом Р = 5 кН со сторонами АВ = 3l, На плиту действуют пара сил с моментом M = 6 кН× м, лежащая в плоскости плиты, и две силы. Значения этих сил, их направления и точки приложения указаны в табл. С3; при этом силы Определить реакции связей в точках А, В и С. При подсчетах принять l = 0, 8
Указания. Задача C3 – на равновесие тела под действием пространственной системы сил. При её решении учесть, что реакция сферического шарнира (или подпятника) имеет три составляющие, а реакция цилиндрического шарнира (подшипника) – две составляющие, лежащие в плоскости, перпендикулярной оси шарнира. При вычислении моментов силы

Пример С3. Вертикальная прямоугольная плита весом Р (рис. С3) закреплена сферическим шарниром в точке A, цилиндрическим (подшипником) в точке В и невесомым стержнем DD¢ , лежащим в плоскости, параллельной плоскости yz. На плиту действуют сила
Дано: Р = 5кН, М =3 кН× м, F1 = 6 кН, F2 = 7, 5 кН, a = 30°, АВ = 1 м, ВС = 2 м, CE = 0, 5АВ, ВК = 0, 5ВС. Определить: реакции опор А, В и стержня DD¢ . Решение
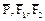 и пара сил с моментом М, а также реакции связей. Реакцию сферического шарнира разложим на три составляющие и пара сил с моментом М, а также реакции связей. Реакцию сферического шарнира разложим на три составляющие  цилиндрического (подшипника) – на две составляющие цилиндрического (подшипника) – на две составляющие  (в плоскости, перпендикулярной оси подшипника), реакцию (в плоскости, перпендикулярной оси подшипника), реакцию  стержня направим вдоль стержня, предполагая, что он растянут. стержня направим вдоль стержня, предполагая, что он растянут.
2 Для определения шести неизвестных реакций составляем шесть уравнений равновесия действующей на плиту пространственной системы сил: å Fkx = 0, XA + F1× cosa = 0, (1) å Fky = 0, YA + YB + F2 - N× cos75° = 0, (2) å Fkz = 0, ZA + ZB - P - N× sin75° + F1× sina = 0, (3)
Для определения момента силы Подставив в составленные уравнения числовые значения всех заданных величин и решив затем эти уравнения, найдем, чему равны искомые реакции. Ответ: XA = -5, 2 кН, YA = 3, 8 кН, ZA = 28, 4 кН, YB = -7, 5 кН, ZB=-12, 4кН,
КИНЕМАТИКА Кинематика – раздел теоретической механики, в которой движение точек или тел изучается с чисто геометрической стороны, без учета их масс и вне зависимости от действующих на них сил. Движение изучается в пространстве и во времени, причем время считается абсолютным (одинаковым во всех системах отсчета).
Кинематика точки Задачей кинематики точки является определение траектории, скорости и ускорения точки. Траекторией точки называется геометрическое место её последовательных положений в пространстве с течением времени относительно рассматриваемой системы координат. По виду траектории движения точки делятся на прямолинейные и криволинейные.
3.1.1 Способы задания движения Задать движение точки – это значит указать способ, позволяющий в любой момент времени определить её положение по отношению к выбранной системе отчета.
1 Векторный способ задания движения. Положение точки по отношению к выбранному центру отсчета будет определено, если для любого момента времени известен её радиус-вектор
2 Координатный способ задания движения. Способ задания движения, заключающийся в задании координат точки как известных функций времени, называется координатным. При рассмотрении движения в прямоугольной декартовой системе координат задаются координаты точки как функции времени (рис. 3.2).
y = f2(t) (3.2) z = f(t)
Ф1(x, y, z)=0, Ф2(x, y, z) = 0 (3.3) Таким образом, траекторией точки в пространстве является линия пересечения поверхностей, описываемых уравнениями (3.3). В случае двумерного (плоского) движения точки уравнения движения и уравнения траектории соответственно имеет вид x = f1(t), y = f2(t); (3.2¢ ) y = f(x) (3.3¢ ) Связь между координатным и векторным способами задания движения. Из рис. 3.3 очевидно, что
S = S(t) (3.5), где S – дуговая координата, отсчитываемая от выбранного начала отсчета на траектории. Знак определяется в соответствии с выбранным направлением отсчета.
Связь между координатным и естественным способами задания движения.
 (3.6) (3.6)
где x, y, z. Знак (+) или (–) перед интегралом ставится в соответствии с выбранным направлением отсчета.
Скорость и ускорение точки 1 При векторном способе задания движения скорость
Ускорение
2 При координатном способе задания движения, когда, в частности, декартовые координаты x, y, z – известные функции времени, сначала определяются проекции скорости на соответствующие декартовые оси
затем – модуль и направляющие косинусы вектора скорости
Декартовые проекции, модуль и направляющие конусы вектора ускорения определяются по формулам:
3 При естественном способе задания движения скорость и ускорение определяются по их проекциям на естественные оси, начало которых находится в движущейся точке, а
Скорость точки как векторную величину можно представить в виде
Ускорение определяется про формулам:
 Здесь Здесь  – единичный вектор касательной, – единичный вектор касательной,  – единичный вектор главной нормали, – единичный вектор главной нормали,  – единичный вектор бинормали, – единичный вектор бинормали,  – соответственно касательное и нормальное составляющие полного ускорения, причем – соответственно касательное и нормальное составляющие полного ускорения, причем  , r – радиус кривизны траектории для т. M, a – направляющий угол полного ускорения. Таким образом, движение точки исследуется в подвижной ортогональной системе координат, начало которых находится в самой движущейся т. M, а их направления определяются ортами , r – радиус кривизны траектории для т. M, a – направляющий угол полного ускорения. Таким образом, движение точки исследуется в подвижной ортогональной системе координат, начало которых находится в самой движущейся т. M, а их направления определяются ортами  В силу такого выбора системы координат третьей составляющей ускорения В силу такого выбора системы координат третьей составляющей ускорения  не будет, т.е. не будет, т.е.  [*]. В этом заключается существенное отличие естественного способа задания движения точки от задания её движения в декартовой системе координат. Естественный способ задания движения часто используется при исследовании криволинейного движения точки и особенно – движений точек вращающихся тел. [*]. В этом заключается существенное отличие естественного способа задания движения точки от задания её движения в декартовой системе координат. Естественный способ задания движения часто используется при исследовании криволинейного движения точки и особенно – движений точек вращающихся тел.
|
Последнее изменение этой страницы: 2017-03-17; Просмотров: 1181; Нарушение авторского права страницы