Бесконечно малые и бесконечно большие функции. Основные теоремы о пределах
КУРС ЛЕКЦИЙ
ПО ДИСЦИПЛИНЕ
«ВЫСШАЯ МАТЕМАТИКА»
Часть 1. Основы математического анализа
§ 1 Функция
1. Основные определения.
О1. Функцией называется закон, по которому каждому значению независимой переменной  , называемой аргументом, ставится в соответствие единственное значение зависимой переменной
, называемой аргументом, ставится в соответствие единственное значение зависимой переменной  , называемой функцией:
, называемой функцией: 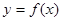 , где
, где  – закон соответствия.
– закон соответствия.
Пример 1.  .
.
О2. Областью определения функции (ООФ:  ) называется множество допустимых действительных значений аргумента, при которых функция имеет смысл в области вещественных чисел; множество значений, которые при этом принимает функция, называется ее областью значений (
) называется множество допустимых действительных значений аргумента, при которых функция имеет смысл в области вещественных чисел; множество значений, которые при этом принимает функция, называется ее областью значений (  ).
).
О3. Геометрическое место точек, абсциссы которых равны значению аргумента, а ординаты – значению функции, называется графиком функции.
О4. Если выполняется равенство  , то функция называется четной, а при выполнении равенства
, то функция называется четной, а при выполнении равенства  – нечетной.
– нечетной.
О5. Если функция не является ни четной, ни нечетной, то она называется функцией общего вида.
Пример 2. 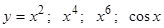 – четные функции;
– четные функции;
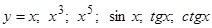 – нечетные функции;
– нечетные функции;
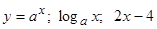 – функции общего вида.
– функции общего вида.
О6. Функция называется периодической, если существует такое вещест-венное число  , что
, что 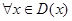 выполняется равенство
выполняется равенство  , при этом меньшее положительное число
, при этом меньшее положительное число  , при котором выполняется указанное равен-ство, называется периодом функции.
, при котором выполняется указанное равен-ство, называется периодом функции.
Пример 3.  , так как
, так как  .
.
О7. Функция называется возрастающей (  ) на интервале
) на интервале 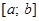 , который в дальнейшем будем называть сегментом, если большему значению аргумента соответствует большее значение функции ( Рис. 54 ).
, который в дальнейшем будем называть сегментом, если большему значению аргумента соответствует большее значение функции ( Рис. 54 ).
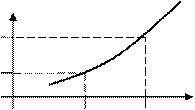

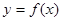
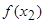
Рис. 54. Пример возрастающей на сегменте
 функции.
функции.


 при
при 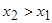 выполняется
выполняется 
О8. Функция называется убывающей (  ) на интервале
) на интервале 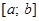 , если большему значению аргумента соответствует меньшее значение функции ( Рис. 55 ).
, если большему значению аргумента соответствует меньшее значение функции ( Рис. 55 ).


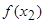

Рис. 55. Пример убывающей на сегменте
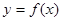 функции.
функции.


 при
при 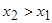 выполняется
выполняется 
О9. Возрастающие или убывающие на сегменте 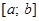 функции объединяются под общим названием монотонные функции.
функции объединяются под общим названием монотонные функции.
Пример 4. Указать интервалы монотонности функции  на сегменте
на сегменте  .
.
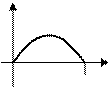

Из рисунка видно, что 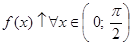 и
и 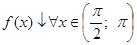 .
.
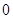


О10. Если на сегменте 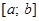 функция не меняет своего значения, то она называется постоянной ( Рис. 57 ).
функция не меняет своего значения, то она называется постоянной ( Рис. 57 ).


 Рис. 57. Постоянная функция.
Рис. 57. Постоянная функция.
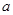
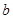

Другие определения теории функций действительной переменной будут вво-диться ниже по мере необходимости.
2. Обратная функция.
Пусть задана функция 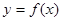 . Если график этой функции пересекает ось абсцисс (
. Если график этой функции пересекает ось абсцисс ( 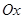 ) в единственной точке, то можно найти такой закон, по которому каждому значению переменной
) в единственной точке, то можно найти такой закон, по которому каждому значению переменной  будет поставлено в соответствие единственное значение переменной
будет поставлено в соответствие единственное значение переменной  , т.е.
, т.е.  . Такой закон соответствия называется обратной функцией.
. Такой закон соответствия называется обратной функцией.
Пример 5. Найти обратную функцию к функции  .
.
Выразив переменную  из этого равенства, найдем обратную функцию
из этого равенства, найдем обратную функцию 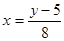 .
.
3. Способы задания функции.
Функция может быть задана одним из следующих способов:
– аналитический, т.е. в виде аналитической формулы (например,  );
);
– графический, т.е. в виде графика для всех значений аргумента  из
из  ;
;
– табличный, т.е. в виде таблицы

– словесный, т.е. функция задается на каждом интервале разными аналитическими формулами, графиком или таблицей, например,  .
.
4. Сложные функции.
Пусть дана функция 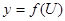 , где
, где  .
.
О11. Функция вида  сложной функцией, а операция ее образования композицией функций или взятием функции от функции.
сложной функцией, а операция ее образования композицией функций или взятием функции от функции.
О12. Функция  называется внутренней, а функция
называется внутренней, а функция  – внешней функциями.
– внешней функциями.
Пример 6.  . В данном примере внутренней функцией является
. В данном примере внутренней функцией является 
 , а внешней функцией будет
, а внешней функцией будет  .
.
Пример 7.  . Внутренней функцией будет
. Внутренней функцией будет  , а внешней функцией является возведение в квадрат.
, а внешней функцией является возведение в квадрат.
Теория пределов
1. Предел последовательности.
О1. Если область определения функции представляет собой ряд натуральных чисел, то область  называется естественной.
называется естественной.
О2. Область значений функции 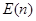 , расположенная в порядке возрастания номера
, расположенная в порядке возрастания номера 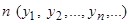 , называется последовательностью и обозначается
, называется последовательностью и обозначается  .
.
Пример 1.
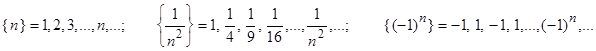 .
.
О3. Число 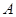 называется пределом последовательности
называется пределом последовательности  , если для любого
, если для любого  существует такой номер
существует такой номер  , что
, что 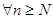 имеет место неравенство
имеет место неравенство 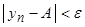 или в другой форме записи
или в другой форме записи 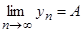 .
.
Приведенное в определении неравенство с модулем можно преобразовать к виду  или
или  .
.



Рис.58. Предел после-
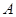
 довательности.
довательности.


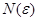

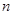
Пример 2. Дана последовательность 
 . Доказать, что пределом этой последовательности является число
. Доказать, что пределом этой последовательности является число 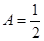 .
.
Возьмем произвольное положительное число 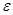 . Найдем такое номер
. Найдем такое номер 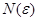 , чтобы
, чтобы 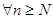 выполнялось неравенство
выполнялось неравенство  , т.е.
, т.е. 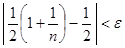 или
или  . Так как
. Так как  , то знак модуля можно снять
, то знак модуля можно снять  . Отсюда
. Отсюда 
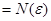 . Если положить
. Если положить  , то
, то  , т.е. начиная с номера
, т.е. начиная с номера  все
все
члены данной последовательности будут попадать в полосу 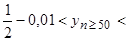
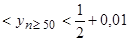 или окончательно
или окончательно  . Отметим, что уменьшение числа
. Отметим, что уменьшение числа 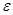 приводит к более узкой полосе внутрь которой попадают члены последовательности, начиная с номера
приводит к более узкой полосе внутрь которой попадают члены последовательности, начиная с номера 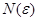 .
.
2. Предел функции.
О4. Окрестностью точки  называется любой интервал, содержащий эту точку.
называется любой интервал, содержащий эту точку.
О5. Интервал, симметричный относительно точки  (
(  ), называется ее
), называется ее 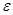 -окрестностью.
-окрестностью.
О6. Если областью определения функции 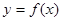 есть множество
есть множество  , то точка
, то точка  называется точкой сгущения, если для любого числа
называется точкой сгущения, если для любого числа  выполняется неравенство
выполняется неравенство  при
при  .
.
З1. Отметим, что точка  может и не принадлежать области
может и не принадлежать области  .
.
О7. Если функция 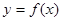 определена на множестве
определена на множестве  с точкой сгущения
с точкой сгущения  , то число
, то число 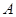 называется пределом функции
называется пределом функции 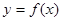 при
при  , если для любого
, если для любого  из выполнения неравенства
из выполнения неравенства  следует выполнение неравенства
следует выполнение неравенства  для любого положительного числа
для любого положительного числа 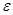 .
.
Обозначение:  .
.
З2. В качестве точки 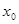 может выступать и бесконечно удаленная точка.
может выступать и бесконечно удаленная точка.
Пример 3. Найти предел функции  при
при  .
.
Перепишем функцию в виде  и построим ее график при
и построим ее график при  (Рис. 59).
(Рис. 59).



Рис. 59. График функции  при
при  .
.

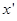
Из рисунка видно, что  , т.е. при
, т.е. при  выполняется неравенство
выполняется неравенство  . Следовательно
. Следовательно 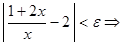
 , отсюда получаем
, отсюда получаем 
 . Итак, если
. Итак, если  , то
, то  . Из рисунка видно, начиная с некоторого значения
. Из рисунка видно, начиная с некоторого значения 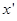 все значения функции
все значения функции  лежат в интервале
лежат в интервале  .
.
О8. Функция  называется ограниченной снизу, если
называется ограниченной снизу, если 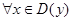 выполняется неравенство
выполняется неравенство 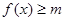 (
( 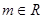 ).Функция
).Функция  называется ограниченной сверху, если
называется ограниченной сверху, если 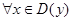 выполняется неравенство
выполняется неравенство  (
(  ). Функция
). Функция  называется ограниченной, если
называется ограниченной, если 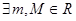 такие, что
такие, что 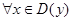 выполняется неравенство
выполняется неравенство 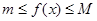 .
.
Пример 4. Ограничена ли функция  ?
?
Так как  , то эта функция ограниченная, причем
, то эта функция ограниченная, причем  ,
,  .
.
Пример 5. Найти предельное значение функции  при
при 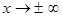 .
.
Построим график заданной функции (Рис. 60):




Рис. 60. График функции  при
при 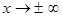 .
.
Из рисунка видно, что при 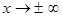 отношение ограниченной функции (
отношение ограниченной функции (  ) к возрастающей по модулю функции (
) к возрастающей по модулю функции (  ) стремится к нулю, следовательно, предельное значение заданной функции
) стремится к нулю, следовательно, предельное значение заданной функции  .
.
3. Односторонние пределы.
О9. Число  называется левосторонним пределом функции
называется левосторонним пределом функции  при стремлении
при стремлении  к
к  слева (
слева (  ), если для любого
), если для любого  существует такое
существует такое  , что
, что 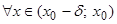 выполняется неравенство
выполняется неравенство  или
или
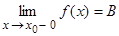 .
.
О10. Число  называется правосторонним пределом функции
называется правосторонним пределом функции  при стремлении
при стремлении  к
к  справа (
справа (  ), если для любого
), если для любого  существует такое
существует такое  , что
, что  выполняется неравенство
выполняется неравенство  или
или
 .
.
Пример 6. Найти лево- и правосторонние пределы функции  .
.
С учетом определения модуля данную функцию можно записать в виде
 . Построим график этой функции (Рис. 61):
. Построим график этой функции (Рис. 61):


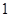 Рис. 61. График функции
Рис. 61. График функции  .
.


Из рисунка видно, что левосторонний предел 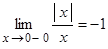 , а правосторонний предел
, а правосторонний предел 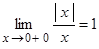 .
.
Пример 7. Вычислить односторонние пределы функции  при
при  .
.
При 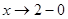 (слева) знаменатель дроби стремится к малой отрицательной величине, следовательно, сама дробь стремится к
(слева) знаменатель дроби стремится к малой отрицательной величине, следовательно, сама дробь стремится к  . При
. При  (справа) знаменатель дроби стремится к малой положительной величине, следовательно, сама дробь стремится к
(справа) знаменатель дроби стремится к малой положительной величине, следовательно, сама дробь стремится к  . Таким образом, левосторонний предел
. Таким образом, левосторонний предел  , а правосторонний предел
, а правосторонний предел  .
.
Пример 8. Найти лево- и правосторонние пределы  при
при  .
.
При  (слева) знаменатель дроби, стоящей в показателе степени экспоненты, стремится к малой отрицательной величине, следовательно, сама дробь стремится к
(слева) знаменатель дроби, стоящей в показателе степени экспоненты, стремится к малой отрицательной величине, следовательно, сама дробь стремится к  . Если аргумент показательной функции с основанием большим единицы стремится к
. Если аргумент показательной функции с основанием большим единицы стремится к  , то сама функция
, то сама функция  (см. график показательной функции в §1 ). При
(см. график показательной функции в §1 ). При  (справа) знаменатель дроби, стоящей в показателе степени экспоненты, стремится к малой положительной величине, следовательно, сама дробь стремится к
(справа) знаменатель дроби, стоящей в показателе степени экспоненты, стремится к малой положительной величине, следовательно, сама дробь стремится к  . Если аргумент показательной функции (основание больше единицы) стремится к
. Если аргумент показательной функции (основание больше единицы) стремится к  , то сама функция
, то сама функция  (см. график показательной функции в §1 ). Таким образом, левосторонний предел
(см. график показательной функции в §1 ). Таким образом, левосторонний предел 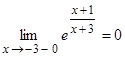 , а правосторонний предел
, а правосторонний предел  .
.
Результаты исследования заносят в сводную таблицу (см. Пример 7).
КУРС ЛЕКЦИЙ
ПО ДИСЦИПЛИНЕ
«ВЫСШАЯ МАТЕМАТИКА»
Часть 1. Основы математического анализа
§ 1 Функция
1. Основные определения.
О1. Функцией называется закон, по которому каждому значению независимой переменной  , называемой аргументом, ставится в соответствие единственное значение зависимой переменной
, называемой аргументом, ставится в соответствие единственное значение зависимой переменной  , называемой функцией:
, называемой функцией: 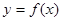 , где
, где  – закон соответствия.
– закон соответствия.
Пример 1.  .
.
О2. Областью определения функции (ООФ:  ) называется множество допустимых действительных значений аргумента, при которых функция имеет смысл в области вещественных чисел; множество значений, которые при этом принимает функция, называется ее областью значений (
) называется множество допустимых действительных значений аргумента, при которых функция имеет смысл в области вещественных чисел; множество значений, которые при этом принимает функция, называется ее областью значений (  ).
).
О3. Геометрическое место точек, абсциссы которых равны значению аргумента, а ординаты – значению функции, называется графиком функции.
О4. Если выполняется равенство  , то функция называется четной, а при выполнении равенства
, то функция называется четной, а при выполнении равенства  – нечетной.
– нечетной.
О5. Если функция не является ни четной, ни нечетной, то она называется функцией общего вида.
Пример 2. 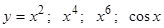 – четные функции;
– четные функции;
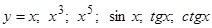 – нечетные функции;
– нечетные функции;
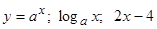 – функции общего вида.
– функции общего вида.
О6. Функция называется периодической, если существует такое вещест-венное число  , что
, что 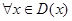 выполняется равенство
выполняется равенство  , при этом меньшее положительное число
, при этом меньшее положительное число  , при котором выполняется указанное равен-ство, называется периодом функции.
, при котором выполняется указанное равен-ство, называется периодом функции.
Пример 3.  , так как
, так как  .
.
О7. Функция называется возрастающей (  ) на интервале
) на интервале 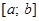 , который в дальнейшем будем называть сегментом, если большему значению аргумента соответствует большее значение функции ( Рис. 54 ).
, который в дальнейшем будем называть сегментом, если большему значению аргумента соответствует большее значение функции ( Рис. 54 ).


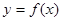
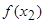
Рис. 54. Пример возрастающей на сегменте
 функции.
функции.


 при
при 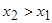 выполняется
выполняется 
О8. Функция называется убывающей (  ) на интервале
) на интервале 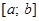 , если большему значению аргумента соответствует меньшее значение функции ( Рис. 55 ).
, если большему значению аргумента соответствует меньшее значение функции ( Рис. 55 ).


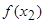

Рис. 55. Пример убывающей на сегменте
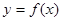 функции.
функции.


 при
при 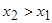 выполняется
выполняется 
О9. Возрастающие или убывающие на сегменте 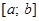 функции объединяются под общим названием монотонные функции.
функции объединяются под общим названием монотонные функции.
Пример 4. Указать интервалы монотонности функции  на сегменте
на сегменте  .
.


Из рисунка видно, что 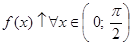 и
и 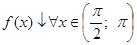 .
.
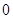


О10. Если на сегменте 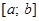 функция не меняет своего значения, то она называется постоянной ( Рис. 57 ).
функция не меняет своего значения, то она называется постоянной ( Рис. 57 ).


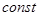 Рис. 57. Постоянная функция.
Рис. 57. Постоянная функция.

Другие определения теории функций действительной переменной будут вво-диться ниже по мере необходимости.
2. Обратная функция.
Пусть задана функция 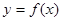 . Если график этой функции пересекает ось абсцисс (
. Если график этой функции пересекает ось абсцисс ( 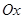 ) в единственной точке, то можно найти такой закон, по которому каждому значению переменной
) в единственной точке, то можно найти такой закон, по которому каждому значению переменной  будет поставлено в соответствие единственное значение переменной
будет поставлено в соответствие единственное значение переменной  , т.е.
, т.е.  . Такой закон соответствия называется обратной функцией.
. Такой закон соответствия называется обратной функцией.
Пример 5. Найти обратную функцию к функции  .
.
Выразив переменную  из этого равенства, найдем обратную функцию
из этого равенства, найдем обратную функцию 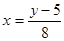 .
.
3. Способы задания функции.
Функция может быть задана одним из следующих способов:
– аналитический, т.е. в виде аналитической формулы (например,  );
);
– графический, т.е. в виде графика для всех значений аргумента  из
из  ;
;
– табличный, т.е. в виде таблицы

– словесный, т.е. функция задается на каждом интервале разными аналитическими формулами, графиком или таблицей, например,  .
.
4. Сложные функции.
Пусть дана функция 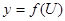 , где
, где  .
.
О11. Функция вида  сложной функцией, а операция ее образования композицией функций или взятием функции от функции.
сложной функцией, а операция ее образования композицией функций или взятием функции от функции.
О12. Функция  называется внутренней, а функция
называется внутренней, а функция  – внешней функциями.
– внешней функциями.
Пример 6.  . В данном примере внутренней функцией является
. В данном примере внутренней функцией является 
 , а внешней функцией будет
, а внешней функцией будет  .
.
Пример 7.  . Внутренней функцией будет
. Внутренней функцией будет  , а внешней функцией является возведение в квадрат.
, а внешней функцией является возведение в квадрат.
Теория пределов
1. Предел последовательности.
О1. Если область определения функции представляет собой ряд натуральных чисел, то область  называется естественной.
называется естественной.
О2. Область значений функции 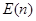 , расположенная в порядке возрастания номера
, расположенная в порядке возрастания номера 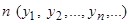 , называется последовательностью и обозначается
, называется последовательностью и обозначается  .
.
Пример 1.
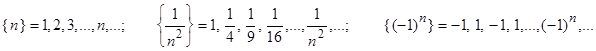 .
.
О3. Число 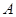 называется пределом последовательности
называется пределом последовательности  , если для любого
, если для любого  существует такой номер
существует такой номер  , что
, что 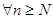 имеет место неравенство
имеет место неравенство 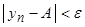 или в другой форме записи
или в другой форме записи 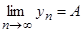 .
.
Приведенное в определении неравенство с модулем можно преобразовать к виду  или
или  .
.



Рис.58. Предел после-
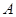
 довательности.
довательности.


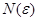

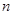
Пример 2. Дана последовательность 
 . Доказать, что пределом этой последовательности является число
. Доказать, что пределом этой последовательности является число 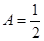 .
.
Возьмем произвольное положительное число 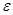 . Найдем такое номер
. Найдем такое номер 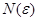 , чтобы
, чтобы 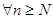 выполнялось неравенство
выполнялось неравенство  , т.е.
, т.е. 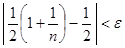 или
или  . Так как
. Так как  , то знак модуля можно снять
, то знак модуля можно снять  . Отсюда
. Отсюда 
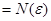 . Если положить
. Если положить  , то
, то  , т.е. начиная с номера
, т.е. начиная с номера  все
все
члены данной последовательности будут попадать в полосу 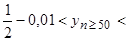
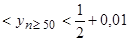 или окончательно
или окончательно  . Отметим, что уменьшение числа
. Отметим, что уменьшение числа 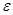 приводит к более узкой полосе внутрь которой попадают члены последовательности, начиная с номера
приводит к более узкой полосе внутрь которой попадают члены последовательности, начиная с номера 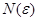 .
.
2. Предел функции.
О4. Окрестностью точки  называется любой интервал, содержащий эту точку.
называется любой интервал, содержащий эту точку.
О5. Интервал, симметричный относительно точки  (
(  ), называется ее
), называется ее 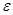 -окрестностью.
-окрестностью.
О6. Если областью определения функции 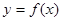 есть множество
есть множество  , то точка
, то точка  называется точкой сгущения, если для любого числа
называется точкой сгущения, если для любого числа  выполняется неравенство
выполняется неравенство  при
при  .
.
З1. Отметим, что точка  может и не принадлежать области
может и не принадлежать области  .
.
О7. Если функция 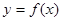 определена на множестве
определена на множестве  с точкой сгущения
с точкой сгущения  , то число
, то число 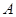 называется пределом функции
называется пределом функции 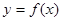 при
при  , если для любого
, если для любого  из выполнения неравенства
из выполнения неравенства  следует выполнение неравенства
следует выполнение неравенства  для любого положительного числа
для любого положительного числа 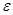 .
.
Обозначение:  .
.
З2. В качестве точки 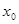 может выступать и бесконечно удаленная точка.
может выступать и бесконечно удаленная точка.
Пример 3. Найти предел функции  при
при  .
.
Перепишем функцию в виде  и построим ее график при
и построим ее график при  (Рис. 59).
(Рис. 59).



Рис. 59. График функции  при
при  .
.

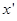
Из рисунка видно, что  , т.е. при
, т.е. при  выполняется неравенство
выполняется неравенство  . Следовательно
. Следовательно 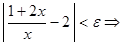
 , отсюда получаем
, отсюда получаем 
 . Итак, если
. Итак, если  , то
, то  . Из рисунка видно, начиная с некоторого значения
. Из рисунка видно, начиная с некоторого значения 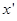 все значения функции
все значения функции  лежат в интервале
лежат в интервале  .
.

