Отношение бесконечно большой функции к ограниченной функции есть бесконечно большая функция.

Установим связь между бесконечно большими и бесконечно малыми функциями, которая дается следующими теоремами:

Т1. Если в некоторой -окрестности точки функция является бесконечно малой функцией, то в этой же окрестности функция ( ) будет бесконечно большой функцией.

Т2. Если в некоторой -окрестности точки функция является бесконечно большой функцией, то в той же самой окрестности функция ( ) будет бесконечно малой функцией.

Эти теоремы очень часто применяются при вычислении пределов, содержащих бесконечно малые и бесконечно большие функции.

3. Основные теоремы о пределах.

Т3. Пусть и . Тогда .

Т4. Пусть и . Тогда .

З6. Иначе данную теорему можно сформулировать так: если функции и и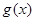меют конечные пределы 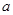и 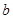, то предел от произведения функций будет равен произведению пределов от этих функций, т.е.

.

Т5. Если в некоторой -окрестности точки функция постоянна и равна ( ), то ее предел равен .

Сл.1 из теорем Т4 и Т5: если , то

, т.е. постоянный множитель можно выносить за знак предела.

Сл.2. Предел степени функции равен степени предела этой функции, т.е.

.

Т6. Пусть и . Тогда .

З6. Сформулируем теорему иначе: если функции и и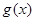меют конечные пределы 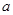и , то предел от отношения функций будет равен отношению пределов от этих функций, т.е. .

4. Вычисление пределов и раскрытие неопределенностей.

Вычисление любых пределов начинается с подстановки предельного значения аргумента в подлимитную функцию . Если при этом получается число, то это число и будет пределом данной функции.

Пример 4. Вычислить .

Подставим в функцию значение , получим . Таким образом, .

Пример 5. Вычислить .

Если подставить в функцию предельное значение , то числитель дроби стремится к , а знаменатель дроби стремится к , т.е. в некоторой -окрестности точки является бесконечно малой функцией. Воспользуемся Т1, величина обратная к бесконечно малой функции есть бесконечно большая функция, предел которой равен бесконечности. Следовательно, .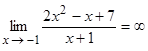

О3. Если при подстановки предельного значения аргумента в подлимитную функцию возникают выражения вида и им подобные, то говорят о наличии неопределенности.

О4. Процесс нахождения пределов, имеющих неопределенность, называется раскрытием неопределенностей.

Рассмотрим некоторые приемы раскрытия неопределенностей.

1. Неопределенность типа 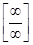, возникающая при вычислении предела от отношения двух полиномов при 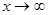( ), раскрывается путем деления числителя и знаменателя на аргумент в высшей степени и использования Т2 о связи бесконечно большой функции с бесконечно малой, предел которой равен 0.

Пример 6. Найти .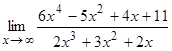

При 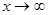и числитель, и знаменатель дроби стремятся к бесконечности, поэтому имеем неопределенность вида 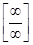. Высший показатель степени равен

 

4 и находится в числителе дроби. Разделим числитель и знаменатель дроби на , получим . Все дроби по Т2 при 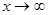стремятся к 0, следовательно, числитель стремится к 6, а знаменатель – к 0. Используя Т1 о связи бесконечно малой функции с бесконечно большой функцией, предел которой равен , окончательно получим, что .

Пример 7. Найти .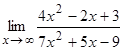

При 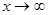и числитель, и знаменатель дроби стремятся к бесконечности, поэтому имеем неопределенность вида 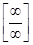. Высший показатель степени равен 2 и находится в числителе и знаменателе дроби. Разделим числитель и знаменатель дроби на , получим . Все дроби по Т2 при 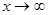стремятся к 0, следовательно, числитель стремится к 4, а знаменатель – к 7. Следовательно, .

Пример 8. Найти .

При 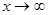и числитель, и знаменатель дроби стремятся к бесконечности, поэтому имеем неопределенность вида 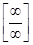. Высший показатель степени равен 3 и находится в знаменателе дроби. Разделим числитель и знаменатель дроби на , получим . Все дроби по Т2 при 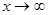стремятся к 0, следовательно, числитель стремится к 0, а знаменатель – к 1. Следовательно, . Рассмотренные примеры позволяют сделать следующий вывод: .

2. Неопределенность типа 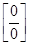, возникающая при вычислении предела от отношения двух полиномов при 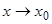( 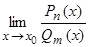), раскрывается путем разложения полиномов на простые множители и дальнейшего сокращения числителя и знаменателя дроби на обнуляющий их множитель .

Пример 9. Найти .

Подстановка предельного значения аргумента в подлимитную функцию приводит к обнулению числителя и знаменателя дроби. Следовательно, дробь приводится к неопределенности 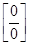. Для раскрытия этой неопределенности разложим числитель и знаменатель дроби на простые множители, для чего решим следующие уравнения: . По теореме Виета находим . Отсюда следует, что , а значит разложение полинома имеет вид: . Решим уравнение:

.

Следовательно, разложение этого полинома на простые множители будет иметь вид: . Подставим найденные разложения полиномов в исходный предел, получим

.

Подставляя вместо переменной ее предельное значение , получим ответ: .

3. Неопределенность типа 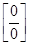, возникающая при вычислении предела, содержащего квадратные корни, при 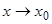раскрывается с использованием формулы, определяющей разность квадратов .

Пример 10. Найти .

Подстановка предельного значения аргумента 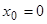в подлимитную функцию приводит к обнулению числителя и знаменателя дроби. Следовательно, дробь приводится к неопределенности 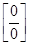. Для раскрытия этой неопределенности умножим числитель и знаменатель дроби на выражение , получим:

.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться: