Проверка гипотезы о равенстве нулю генерального
Коэффициента ранговой корреляции Спирмена и Кендала
Требуется при заданном уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента ранговой корреляции Спирмена ρ г при конкурирующей гипотезе Н1: ρ г ≠ 0. Для этого найдем критическую точку:
, (13)
где п – объем выборки, ρ В – выборочный коэффициент ранговой корреляции Спирмена, tкр (α, k) – критическая точка двусторонней критической области, найденная по таблице критических точек распределения Стьюдента, число степеней свободы k = n – 2. Тогда, если | ρ B | < Tкр, то нулевая гипотеза принимается, то есть ранговая корреляционная связь между признаками незначима. Если | ρ B | > Tкр, то нулевая гипотеза отвергается, и между признаками существует значимая ранговая корреляционная связь.
Для проверки нулевой гипотезы Н0: τ г = 0 (генеральный коэффициент ранговой корреляции Кендалла равен нулю) при альтернативной гипотезе Н1: τ г ≠ 0 необходимо найти критическую точку:
, (14)
где п – объем выборки, а zкр – критическая точка двусторонней критической области, определяемая из условия 
по таблицам для функции Лапласа. Если | τ B | < Tкр , то нулевая гипотеза принимается (ранговая корреляционная связь между признаками незначима). Если | τ B | > Tкр , то нулевая гипотеза отвергается (между признаками существует значимая ранговая корреляционная связь).
Вопросы для самопроверки
1. Что такое критерий согласия?
2. Какие критерии согласия Вы знаете?
3. Опишите схему применения критерия Пирсона.
4. Запишите плотность распределения закона 
с 
степенью свободы.
5. Могут ли опытные данные одновременно согласовываться с несколькими гипотезами о законе распределения?
ПРИМЕНЕНИЕ В МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
ПРОГРАММЫ EXCEL
а). Структура данных, преобразование данных. Ячейки, диапазон ячеек. Ячейки нумеруются одновременным заданием имени столбца и номером элемента в этом столбце. Например, A3 –это третья сверху ячейка, находящаяся в первом столбце.
Нужные данные для обработки задаются указанием их верхней правой и нижней левой границ в массиве всех данных. Например, оператор (A1: C8) выделит первые восемь элементов в столбцах A, B, C.
Формулы, способы их задания.Для задания формул, по которых будут проводиться вычисления с элементами массивов, имеется специальная строка (в верхней половине окна, она начинается сразу после символа fx). В EXCEL существуют различные группы формул, для наших целей наиболее важны такие: МАТЕМАТИЧЕСКИЕ, МАТ. и ТРИГОНОМЕТРИЯ, ССЫЛКИ И МАССИВЫ, а также СТАТИСТИЧЕСКИЕ, о которых подробнее будет сказано ниже. Результат вычислений функции помещается в заранее выбранную ячейку.
Статистические формулы. Список реализованных в EXCEL статистических команд можно получить, нажав значок fxи выбрав там пункт СТАТИСТИЧЕСКИЕ ФУНКЦИИ. Выделив нужную статистическую функцию, можно получить по ней справку (для этого – имеется предложение в нижней левой части появившегося окна - СПРАВКА ПО ЭТОЙ ФУНКЦИИ).
б). Основные распределения.Команды НОРМРАСП и НОРМОБР вычисляют значения для нормального распределения и для обратной ему функции. Например, команда НОРМОБР(0.12, 2, 0.5) дает значение, соответствующее значению вероятности 0.12 для нормального закона распределения со средним значением (математическим ожиданием), равным 2 и среднеквадратичным отклонением, равным 0.5. Некоторые другие распределения – это ПУАССОН, СТЬЮРАСП, БИНОМРАСП.
в). Вычисление оценок. Перечислим некоторые нужные нам основные команды:
СРЗНАЧ– вычисление среднего арифметического заданного массива данных (строки, столбца, матрицы и др.). Дает оценку для математического ожидания.
ДИСП (несмещенная оценка дисперсии, ее допустимо применять только для больших наборов данных – не менее 30, в противном случае нужно применять команду ДИСПР).
Пример: ДИСП(А1: А30) – вычисление несмещенной оценки дисперсии для 30 чисел из столбца A.
СТАНДОТКЛ, СРОТКЛ (несмещенная оценка) – это фактически корни квадратные 
и 
из соответствующих оценок дисперсии.
г). Построение гистограммы.Гистограмма дает возможность приближенно определить вид графика плотности распределения изучаемой случайной величины. Например, если гистограмма напоминает собой гауссову кривую (хоть и состоит из горизонтальных отрезков), то можно предполагать, что изучаемая случайная величина распределена нормально (для более точного исследования на нормальность имеются специальные методы).
Для построения гистограммы можно использовать специальную кнопку в основном меню: «Мастер диаграмм» (гистограмма тут рассматривается как одна из многих диаграмм в EXCEL). Шаг за шагом, отвечая на задаваемые «Мастером диаграмм» вопросы, получим гистограмму.
д). Корреляция. Простая регрессия. Основные команды:
ПИРСОН– вычисляет коэффициент корреляции (здесь он фигурирует как коэффициент Пирсона). Например, команда ПИРСОН(A1: A10; B1: B10) дает коэффициент корреляции для двух столбцов A и B.
КВПИРСОН - дает квадрат коэффициента корреляции.
КОРРЕЛ – дает тот же коэффициент корреляции.
НАКЛОН, ОТРЕЗОК, ЛИНЕЙН– команды для построения прямой регрессии и анализа ее точности.
Для уравнения линейной регрессии y=ax+b команда НАКЛОН дает коэффициент a, ОТРЕЗОК дает коэффициент b. Формат этих команд одинаков, например, НАКЛОН(A1: A10; B1: B10) дает наклон прямой регрессии столбца A зависимых значений на столбец независимых значений B.
Команда ЛИНЕЙН позволяет не только находить линейную регрессию, но и вычислять различные дополнительные параметры для ее анализа, а также проводить и кратную регрессию.
е). Кратная регрессия – производится с помощью команды ЛИНЕЙН. Например, ЛИНЕЙН(Y, X) решает задачу для массивов Y - зависимых данных (столбец) и X - независимых данных (один или несколько столбцов), выделяемых стандартным для EXCEL методом. Дополнительно можно задавать некоторые специальные опции.
Приложение.
Таблица 1. Значения функции Лапласа
| X
| Ф(х)
| X
| Ф(х)
| X
| Ф(х)
| X
| Ф(х)
|
| 0.00
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.10
0.11
0.12
0.13
0.14
0.15
0.16
0.17
0.18
0.19
0.20
0.21
0.22
0.23
0.24
0.25
0.26
0.27
0.28
0.29
0.30
0.31
| 0.0000
0.0040
0.0080
0.0120
0.0160
0.0199
0.0239
0.0279
0.0319
0.0359
0.0398
0.0438
0.0478
0.0517
0.0557
0.0596
0.0636
0.0675
0.0714
0.0753
0.0793
0.0832
0.0871
0.0910
0.0948
0.0987
0.1026
0.1064
0.1103
0.1141
0.1179
0.1217
| 0.32
0.33
0.34
0.35
0.36
0.37
0.38
0.39
0.40
0.41
0.42
0.43
0.44
0.45
0.46
0.47
0.48
0.49
0.50
0.51
0.52
0.53
0.54
0.55
0.56
0.57
0.58
0.59
0.60
0.61
0.62
0.63
| 0.1255
0.1293
0.1331
0 1368
0.1406
0.1443
0.1480
0.1517
0.1554
0.1591
0.1628
0.1664
0.1700
0.1736
0.1772
0.1808
0.1844
0.1879
0.1915
0.1950
0.1985
0.2019
0.2054
0.2088
0.2123
0.2157
0.2190
0.2224
0.2257
0.2291
0.2324
0.2357
| 0.64
0.65
0.66
0.67
0.69
0.70
0.71
0.72
0.73
0.74
0.75
0.76
0.77
0.78
0.79
0.80
0.81
0.82
0.83
0.84
0.85
0.86
0.87
0.88
0.89
0.90
0.91
0.92
0.93
0.94
0.95
| 0.2389
0.2422
0.2454
0.2486
0.2517
0.2549
0.2580
0.2611
0.2642
0.2673
0.2703
0.2734
0.2764
0.2794
0.2823
0.2852
0.2881
0.2910
0.2939
0.2967
0.2995
0 3023
0.3051
0.3078
0.3106
0.3133
0.3159
0.3186
0.3212
0.3238
0.3264
0.3289
| 0.96
0.97
0.98
0.99
1.00
1, 01
1.02
1.03
1.04
1.05
1.06
1.07
1.08
1.09
1.10
1.11
1.12
1.13
1.14
1.15
1.16
1.17
1.18
1.19
1.20
1.21
1.22
1.23
1.24
1.25
|
0.3340
0.3365
0.3389
0.3461
0.3485
0.3508
0.3554
0.3577
0.3621
0.3643
0.3708.
0.3729
0.3749
0.3770
0.3790
0.3810
0.3830
0.3849
0.3869
0/3883
0.3907
0.3925
0.3944
|
Продолжение таблицы 1.
| X
| Ф(х)
| X
| Ф(х)
| X
| Ф(Х)
| X
| Ф(х)
|
| 1.26
1.27
1.28
1.29
1.30
1.31
1 32
1.33
1.34
1.35
1.36
1.37
1.38
1.39
1.40
1.41
1.42
1.43
1.44
1 45
1.46
1.47
1.48
1.49
1.50
1.51
1.52
1.53
1.54
1.55
1 56
1.57
1.58
| 0.3962
0.3980
0.4015
0.4032
0.4049
0.4066
0.4082
0.4099
0.4115
0.4131
0.4147
0.4162
0.4177
0.4192
0.4207
0.4222
0.4236
0.4251
0.4265
0.4279
0.4292
0.4306
0.4319
0, 4332
0.4345
0.4357
0.4370
0.4382
0.4394
0.4406
0 4418
0.4429
| 1.59
1 60
1.61
1.62
1.63
1.64
1.65
1.66
1.67
1.68
1.69
1.70
1.71
1.72
1.73
1.74
1.75
1.76
1.77
1.78
1.79
1.80
1.81
1.82
1.83
1.84
1.85
1.86
1.87
1.88
1.89
1.90
1.91
| 0.4441
0.4452
0.4463
0.4474
0.4484
0.4495
0.4505
0.4515
0.4525
0.4535
0.4545
0.4554
0.4564
0.4573
0.4582
0.4591
0.4599
0.4608
0.4616
0.4625
0.4633
0.4641
0.4649
0.4656
0.4664
0.4671
0.4678
0.4686
0.4693
0.4699
0.4706
0.4713
0.4719
| 1.92
1.93
1.94
1.95
1.96
1.97
1.98
1.99
2.00
2.02
2.04
2.06
2.08
2.10
2.12
2.14
2.16
2.18
2.20
2.22
2.24
2.26
2.28
2.30
2.32
2.34
2.36
2.38
2.40
2.42
2.44
2.46
2.48
| 0.4726
0.4732
0.4738
0.4744
0.4750
0.4756
0.4761
0.4767
0.4772
0.4783
0.4793
0.4803
0.4812
0.4821
0.4830
0.4838
0.4846
0.4854
0.4861
0.4868
0.4875
0.4881
0.4887
0.4893
0.4898
0.4904
0.4909
0.4913
0.4918
0.4922
0.4927
0.4931
0.4934
| 2.50
2.52
2.54
2.56
2.58
2.60
2.62
2.64
2.66
2.68
2.70
2.72
2.74
2.76
2.78
2.80
2.82
2.84
2.86
2.88
2.90
2.92
2.94
2.96
2.98
3.00
3.20
3.40
3 60
3.80
4.00
4.50
5.00
| 0.4938
0.4941
0.4945
0.4948
0, 4951
0.4953
0.4956
0.4959
0.4961
0.4963
0.4965
0.4967
0.4969
0.4971
0.4973
0.4974
0.4976
0.4977
0.4979
0.4980
0.4981
0.4982
0.4984
0.4985
0.4986
0.49865
0.49931
0.49966
0.49984
0.49992
0.49996
0.49999
0.49999
|
Таблица 2. Критические точки распределения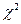 
| Число степеней свободы k
| Уровень значимости 
|
| 0.01
| 0.025
| 0.05
| 0.95
| 0.975
| 0.99
|
|
| 6.6
9.2
11.3
13.3
15.1
16.8
18.5
20.1
21.7
23.2
24.7
26.2
27.7
29.1
30.6
32.0
33.4
34.8
36.2
37.6
38.9
40.3
41.6
43.0
44.3
45.6
47.0
48.3
49.6
50.9
| 5.0
7.4
9.4
11.1
12.8
14.4
16.0
17.5
19.0
20.5
21.9
23.3
24.7
26.1
27.5
28.8
30.2
31.5
32.9
34.2
35.5
36.8
38.1
39.4
40.6
41.9
43.2
44.5
45.7
47.0
| 3.8
6.0
7.8
9.5
11.1
12.6
14 1
15.5
16.9
18.3
19.7
21.0
22.4
23.7
25.0
26.3
27.6
28.9
30.1
31.4
32.7
33.9
35.2
36.4
37.7
38.9
40.1
41.3
42.6
43.8
| 0.0039
0.103 0.352
0.711
1.15
1.64
2.17
2.73
3.33
3.94
4.57
5.23
5.89
6.57
7.26
7.96
8.67
9.39
10.1
10.9
11.6
12.3
13.1
13.8
14.6
15.4
16.2
16.9
17.7
18.5
| 0.00098
0.051 0.216
0.484
0.831
1.24
1.69
2.18
2.70
3.25
3.82
4.40
5.01
5.63
6.26
6.91
7.56
8.23
8.91
9.59
10.3
11.0
11.7
12.4
13.1
13.8
14.6
15.3
16.0
16.8
| 0.00016
0.020 0.115
0.297
0.554 0.872
1.24
1.65
2.09
2.56
3.05
3.57
4.11
4.66
5.23 5.81
6.41
7.01 7.63 8.26 8.90 9.54
10.2
10.9 11.5
12.2 12.9 13.6
14.3
15.0
|
Таблица 3. Критические точки распределения Стьюдента
| Число степеней
свободы k
| Уровень значимости (двусторонняя критическая область)
|
| 0.10
| 0.05
| 0.02
| 0.01
| 0.002
| 0.001
|
|
∞
| 6.31
2.92
2.35
2.13
2.01
1.89
1.86
1.83
1.81
1.80
1.78
1.77
1.76
1.75
1.75
1.74
1.73
1.73
1.73
1.72
1.72
1.71
1.71
1.71
1.71
1.71
1.70
1.70
1.70
1.68
1.67
1.66
1.64
| 12.7
4.30
3.18
2.78
2.57
2.45'
2.36
2.31
2.26
2.23
2.20
2.18
2.16
2.14
2.13
2.12
2.11
2.10
2.09
2.09
2.08
2.07
2.07
2.06
2.06
2.06
2.05
2.05
2.05
2.04
2.02
2.00
1.98
1.96
| 31.82
6.97
4.54
3.75
3.37
3.14
3.00
2.90
2.82
2.76
2.72
2.68
2.65
2.62
2.60
2.58
2.57
2.55
2.54
2.53
2.52
2.51
2.50
2.49
2.49
2.48
2.47
2.46
2.46
2.46
2.42
2.39
2.36
2.33
| 63.7
9.92
5.84
4.60
4.03
3.71
3.50
3.36
3.25
3.17
3.11
3.05
3.01
2.98
2.95
2.92
2.90
2.88
2.86
2.85
2.83
2.82
2.81
2.80
2.79
2.78
2.77
2.76
2.76
2.75
2.70
2.66
2.62
2.58
| 318.3
22.33
10.22
7.17
5.89
5.21
4.79
4.50
4.30
4.14
4.03
3.93
3.85
3.79
3.73
3.69
3.65
3.61
3.58
3.55
3.53
3.51
3.59
3.47
3.45
3.44
3.42
3.40
3.40
3.39
3.31
3.23
3.17
3.09
| 637.0
31.6
12.9
8.61
6.86
5.96
5.40
5.04
4.78
4.59
4.44
4.32
4.22
4.14
4.07
4.01
3.95
3.92
3.88
3.85
3.82
3.79
3.77
3.74
3.72
3.71
3.69
3.66
3.65
3.55
3.46
3.37
3.29
|
| 0.05
| 0.025
| 0.01
| 0.005
| 0.001
| 0.0005
|
| Уровень значимости (односторонняя критическая область)
|
Таблица 4. Критические точки распределения Фишера
( 
– число степеней свободы большей дисперсии, 
– число степеней свободы меньшей дисперсии)
| Уровень значимости = 0.01
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
98.49
34.12
21.20
16.26
13.74
12.25
11.26
10.56
10.04
9.86
9.33
9, 07
8.86
8.68
8.53
8.40
|
99.01
30.81
18.00
13.27
10.92
9.55
8.65
8.02
7.56
7.20
6.93
6.70
6.51
6.36
6.23
6.11
|
90.17
29.46
16.69
12.06
9.78
8.45
7.59
6.99
6.55
6.22
5.95
5.74
5.56
5.42
5.29
5.18
|
99.25
28.71
15.98
11.39
9.15
7.85
7.01
6.42
5.99
5.67
5.41
5.20
5.03
4.89
4.77
4.67
|
99.33
28.24
15.52
10.97
8.75
7.46
6.63
6.06
5.64
5.32
5.06
4.86
4.69
4.56
4.44
4.34
|
99.30
27.91
15.21
10.67
8.47
7.19
6.37
5.80
5.39
5.07
4.82
4.62
4.46
4.32
4.20
4.10
|
99.34
27.67
14.98
10.45
8.26
7.00
6.19
5.62
5.21
4.88
4.65
4.44
4.28
4.14
4.03
3.93
|
99.36
27.49
14.80
10.27
8.10
6.84
6.03
5.47
5.06
4.74
4.50
4.30
4.14
4.00
3.89
3.79
|
99.36
27.34
14.66
10.15
7.98
6.71
5.91
5.35
4.95
4.63
4.39
4.19
4.03
3.89
3.78
3.68
|
99.40
27.23
14.54
10.05
7.87
6.62
5.82
5.26
4.85
4.54
4.30
4.10
3.94
3.80
3.69
3.59
|
99.41
27.13
14.45
9.96
7.79
6.54
5.74
5.18
4.78
4.46
4.22
4.02
3.86
3.73
3.61
3.52
|
99.42
27.05
14.37
9.89
7.72
6.47
5.67
5.11
4.71
4.40
4.16
3.96
3.80
3.67
3.55
3.45
|
Продолжение таблицы 4
| Уровень значимости = 0.05
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 18.5
| 19.0
| 19.16
| 19.25
| 19: 30
| 19.33
| 19.36
| 19.37
| 19.38
|
|
| 19.41
|
|
| 10.13
| 9.55
| 9.28
| 9.12
| 9.01
| 8.94
| 8.88
| 8.84
| 8.81
| 8.78
| 8.76
| 8.74
|
|
| 7.71
|
| 6.59
| 6.39
| 6.26
| 6 16
| 6.09
| 6.04
| 6.00
| 5.96
| 5.93
| 5.91
|
|
| 6.61
| 5.79
| 5.41
| 5.19
| 5.05
| 4.95
| 4.88
| 4.82
| 4.78
| 4.74
| 4.70
| 4.68
|
|
| 9.99
| 5.14
| 4.76
| 4.53
| 4.39
| 4.28
| 4.21
| 4.15
| 4.10
| 4.06
| 4.03
| 4.00
|
|
| 5.59
| 4.74
| 4.35
| 4.12
| 3.97
| 3.87
| 3.79
| 3.73
| 3.68
| 3.63
| 3.60
| 3.57
|
|
| 5.32
| 4.46
| 4.07
| 3.84
| 3.69
| 3.58
| 3.50
| 3.44
| 3.39
| 3.34
| 3.31
| 3.28
|
|
| 5.12
| 4.26
| 3.86
| 3.63
| 3.48
| 3.37
| 3.29
| 3.23
| 3.18
| 3.13
| 3.10
| 3.07
|
|
| 4.96
| 4.10
| 3.71
| 3 48
| 3.33
| 3.22
| 3.14
| 3.07
| 3.02
| 2.97
| 2.94
| 2.91
|
|
| 4.84
| 3.98
| 3.59
| 3.36
| 3.20
| 3.09
| 3.01
| 2.95
| 2.90
| 2.86
| 2.82
| 2.79
|
|
| 4.75
| 3.88
| 3.49
| 3.26
| 3.11
| 3.00
| 2.92
| 2.85
| 2.80
| 2.76
| 2.72
| 2.69
|
|
| 4.67
| 3.80
| 3.41
| 3.18
| 3.02
| 2.92
| 2.84
| 2.77
| 2.72
| 2.67
| 2.63
| 2.60
|
|
| 4.60
| 3.74
| 3.34
| 3.11
| 2.96
| 2.85
| 2.77
| 2.70
| 2.65
| 2.60
| 2.56
| 2.53
|
|
| 4.54
| 3.68
| 3.29
| 3.06
| 2.90
| 2.79
| 2.70
| 2.64
| 2.59
| 2.55
| 2.51
| 2.48
|
|
| 4.49
| 3.63
| 3.24
| 3.01
| 2.85
| 2.74
| 2.66
| 2.59
| 2.54
| 2.49
| 2.45
| 2.42
|
|
| 4.45
| 3.59
| 3.20
| 2.96
| 2.81
| 2.70
| 2, 62
| 2.55
| 2.50
| 2.45
| 2.41
| 2.38
|
