
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Операция антиэквиваленции
Пример 1: составить таблицу истинности для выражения ( P®Q ) & P Формула содержит 2 переменные – P и Q, следовательно, в таблице истинности (табл. 1.8.) буде 22 = 4 строки. Расставим приоритеты операций: первое действие – импликация, второе действие – конъюнкция. Таблица 1.8.
Пример 2: составить таблицу истинности для выражения ((A ® ù B) & C) « (( ù (A&B)&C) Формула содержит 3 переменные – A , В, С, следовательно, в таблице истинности (табл. 1.8.) буде 23 = 8 строк. Расставим приоритеты операций:
Таблица 1.9.
1.3. Равносильность формул. Пусть имеются две формулы: А ( x 1 , …, х n ) и B ( x 1 , …, xn ). Формулы называются равносильными, если они принимают одни и те же значение на всех наборах значений переменных х1, …, хп. Другими словами, формулы равносильны, если результирующие значения их таблиц истинности совпадают. Факт равносильности обозначают «eq». Важнейшие равносильности алгебры логики можно разбить на три группы. Основные формулы равносильности: 1. C Ú Л eq X 2. X Ú И eq И 3. X & И eq X 4. C & Л eq Л 5. C & ù C eq Л - закон противоречия 6. 7.
8. C & C & ... & C eq X 9. ùù C eq Х - закон снятия двойного отрицания 10.
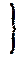 Х & ( C Ú Y ) eq Х Х & ( C Ú Y ) eq Х
11. Х Ú ( C & U ) eq Х Формулы равносильности, выражающие одни логические операции через другие: 12. C ® U eq ù C Ú Y 13. C ® U eq ù ( C & ù U ) 14. C « U eq ( C ® U ) & ( U ® C ) 15. C « U eq ( ù C & ù U ) V(X&Y) 16. 17. ù ( C Ú Y ) eq ù C & ù U 18.
19. ù ( C & U ) eq ù C Ú ù U 20. ù ( ù C & ù U ) eq X Ú Y Формулы равносильности, выражающие основные законы алгебры логики: 21. C Ú Y eq Y Ú X – коммутативность дизъюнкции; 22. C & U eq U & C - коммутативность дизъюнкции; 23. ( X Ú Y ) Ú Z eq X Ú ( Y Ú Z ) eq X Ú Y Ú Z – ассоциативность дизъюнкции; 24. ( X & Y ) & Z eq X & ( Y & Z ) eq X & Y & Z – ассоциативность конъюнкции; 25. C & ( U Ú Z ) eq ( X & Y ) Ú ( X & Z ) - дистрибутивность конъюнкции относительно дизъюнкции; 26. X Ú (Y&Z) eq (X Ú Y)&(X Ú Z) - дистрибутивность дизъюнкции относительно конъюнкции; Используя формулы равносильных преобразований 1-26, часть формулы или всю формулу можно заменить равносильной ей формулой. Такие преобразования называются равносильными. Пример 3: доказать равносильность формул Х →(X & ù (Y Ú Z)) (1) ù X Ú ( ù Y & ù Z) (2) составив таблицы истинности для них, а также проведя равносильные преобразования. Поскольку в каждой формуле содержится 3 переменных, строк в таблицах истинности для каждой формулы будет 23=8. Составим таблицы истинности для обеих формул (табл. 1.10, 1.11): Таблица 1.10 Таблица истинности для формулы (1)
Таблица 1.11 Таблица истинности для формулы (2)
Из таблиц истинности формул 1.10, 1.11 видно, что истинностные значения формул, находящихся в результирующих столбцах каждой из таблиц, совпадают. Теперь докажем равносильность этих двух формул, используя равносильные преобразования (в этом примере в скобках указан номер формулы равносильности, на основании которой проведено преобразование) Х→( X & ù ( Y Ú Z )) eq (17) Х→( X & ( ù Y & ù Z )) eq (12) ù X Ú (X & ( ù Y& ù Z)) eq (26) ( ù X Ú X) & ( ù X Ú ( ù Y& ù Z)) eq(6) И & ( ù X Ú ( ù Y & ù Z )) eq (3) ( ù X Ú ( ù Y & ù Z )) 1.4. Закон двойственности Операции конъюнкции является двойственной по отношению к операции дизъюнкции, а операции дизъюнкции – двойственна по отношению к операции конъюнкции. Если А(х1, …, хп) - некоторая формула алгебры логики, то формула, полученная из нее заменой всех операций двойственными им, называется двойственной формулой для А и обозначается А * (х1, …,хп) . Например, для формулы А º (х Ú y )& z двойственной будет формула А * º (х & y ) Ú z Преобразования двойственности являются обратимыми, т.е. (А * ) * =А Утверждение1: Любая операции может быть представлена через дизъюнкцию, конъюнкцию и отрицание. Утверждение2: Если для записи некоторой формулы алгебры логики А используются только знаки операции отрицания, конъюнкции и дизъюнкции, то отрицание такой формулы равносильно двойственной формуле от отрицания всех входящих в нее переменных. ù А(х1, …, хп) eq А*( ù х1, …, ù хп) А(х1, …, хп) eq ù А*( ù х1, …, ù хп) Утверждение равносильности: если две формулы равносильны, то равносильны и двойственные им: A eq B « (A* eq B*) (A* eq B*) « A eq B 1.5. Тавтологии, противоречия и выполнимые формулы. Формула, которая принимает значение истина при любых наборах входящих в нее переменных, называется тавтологией (тождественно истинной, общезначимой). Для указания на тавтологию используют знак «D ». Например: D(P®Q)&(Q®R)&P®R Формула, которая принимает значение «ложь» при любых наборах значений входящих в нее переменных, называется противоречием (тождественно ложной). Формула, принимающая значение «истина» на одних наборах переменных и значение «ложь» на других, называется выполнимой. Различные формулы, полученные подстановками других формул в тавтологию, не зависимо от их конкретного содействия, всегда являются истинными в силу одной только своей структуры. Иначе говоря, тавтологии можно рассматривать как некоторые логически-истинные схемы рассуждений или доказательств. Поэтому тавтологии играют роль законов в логике высказываний и претендуют на установление методов постановления правильных умозаключений. Существует бесконечное множество тавтологий, а, значит, и законов логики высказываний. В классической логике наиболее часто используются следующие законы: 1. Закон тождества ᅣ P ® P 2. Закон исключенного третьего ᅣ P Ú ù P 3. Закон противоречия ᅣ ù ( P & ù P ) 4. Закон двойного отрицания ᅣ ùù P « P 5. Закон добавления антецедента (в популярной литературе: истина из чего угодно) ᅣ P ® ( Q ® P ) 6. Из ложного что угодно ᅣ ù P ® ( P ® Q ) 7. Закон отделения ᅣ ( P ® Q ) & P ® Q (Если из некоторого P следует Q, и существует P, то существует Q) 8. Закон от противного ᅣ ( P ® Q ) & ù Q ® ù P 9. Закон силлогизма ᅣ ( P ® Q ) & ( Q ® R ) ® ( P ® R ) 10. Закон контрпозиции ᅣ ( P ® Q ) ® ( ù Q ® ù P ) Каждый из законов логики высказываний отображает в символической форме некоторую схему доказательства. Например: 1) В соответствии с законом отделения: если истинно, что из некоторого высказывания P следует высказывание Q, и, кроме того, P является истиной, то истиной будет и Q. 2) В соответствии с законом от противного. Закон от противного применяется при доказательстве от противного, а именно, желая доказать утверждение P, мы предполагаем, что P - ложно и доказываем (выводим, что из P следует некоторое высказывание Q, о котором известно, что оно ложно (значит, ù Q -истина)). Отсюда заключаем, что P должно быть истиной. Утверждение, связывающее равносильность с эквиваленцией . ( ᅣ А « В) « (А eq В) Тавтологии можно получать из равносильной замены «eq» на ««» и наоборот. 1.6. Проблема разрешимости Как было сказано ранее, каждую формулу можно отнести к одному из классу: или тождественно истинные, или тождественно ложные, или выполнимые. В связи с этим возникает вопрос, каким образом определить, к какому классу относится формула, не составляя таблиц истинности. Ведь практическое использование таблиц истинности для формул с большим количеством переменных весьма трудоемкий процесс. Эта задача и носит название проблемы разрешимости. Возможно преобразовать формулу к некоторому стандартному виду, обеспечивающему простоту и эффективность проверки при определенности истинных значений всех входящих в формулу переменных. Существует ряд методов решения сформулированной проблемы. Рассмотрим метод приведения к нормальным формам. Нормальные формы. Назовем элементарной конъюнкцией такую конъюнкцию, которая содержит только переменные и их отрицания. Например, формула ( X & ù Y & P & ù X ) является элементарной конъюнкцией. Назовем элементарной дизъюнкцией такую дизъюнкцию, которая содержит только переменные и их отрицания. Например, формула ( X Ú ù Y Ú P Ú ù Z ) является элементарной дизъюнкцией. Формула, равносильная некоторой формуле Á и представляющая собой дизъюнкцию элементарных конъюнкций, называется дизъюнктивной нормальной форма (ДНФ) формулы Á. Например, формула ( X & ù Y & Z ) Ú ( X & ù Z & P ) Ú ( ù Y & Z & ù P ) является дизъюнктивной нормальной формой. Формула, равносильная некоторой формуле Á и представляющая собой конъюнкцию элементарных дизъюнкций называется конъюнктивной нормальной формой (КНФ) формулы Á. Например, формула ( X Ú ù Y Ú Z ) & ( P Ú ù Q Ú ù Z Ú Y ) & ( X Ú ù P Ú Q ) является конъюнктивной нормальной формой. Утверждения: 8 Для того чтобы элементарная дизъюнкция была тождественно истинной, необходимо и достаточно, чтобы она содержала хотя бы одну пару - переменную и ее отрицание. 8 Для того чтобы элементарная конъюнкция была тождественно ложной, необходимо и достаточно, чтобы она содержала хотя бы одну пару переменной и ее отрицания 8 Любая формула исчисления высказываний имеет равносильную дизъюнктивную и конъюнктивную нормальные формы. 8 Для того чтобы ДНФ была тождественно ложной, необходимо, чтобы все входящие в нее элементарные конъюнкции были тождественно ложными. То есть каждая элементарная конъюнкция, входящая в ДНФ должна содержать хотя бы одну пару- переменную и ее отрицание. 8 Для того чтобы КНФ была тождественно истинной, необходимо чтобы все, входящие в нее элементарные дизъюнкции были тождественно истинными. То есть, каждая элементарная дизъюнкция, образующая КНФ должна содержать хотя бы одну пару- переменную и ее отрицание. Если в каждом члене нормальной формы представлены все переменные прямо или с отрицанием, то она называется совершенной нормальной формой (СДНФ, СКНФ). Утверждение: Для любой формулы существует одна и только одна СДНФ и одна СКНФ. Существуют доказательства как выше приведенных утверждений, так и далее сформулированных утверждений, которые не будут приведены, так как основной задачей курса является использование аппарата формальной логики. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Последнее изменение этой страницы: 2019-03-22; Просмотров: 296; Нарушение авторского права страницы