Класифікація рівнянь в частинних похідних.

Класифікація рівнянь в частинних похідних.

Класифікують рівняння в частинних похідних по багатьох ознаках, а саме, приймаючи до уваги:

1. Порядок рівняння – найвищий порядок частинної похідної, що входить в рівняння;

2. Число змінних – число незалежних змінних рівняння;

3. Лінійність чи нелінійність відносно шуканої функції чи її похідних;

4. Однорідність чи неоднорідність (тобто рівний нулю чи ні той член рівняння, який суттєво не містить невідомої функції чи її похідних);

5. Види коефіцієнтів, відносно яких рівняння поділяють на рівняння з постійними коефіцієнтами та рівняння зі змінними коефіцієнтами.

6. Нехай шукана функція U залежить від n незалежних змінних:

Означення 1. Рівність виду

, (1.1)

яка зв’язує шукану функцію U, незалежні змінні і частинні похідні від шуканої функції, називають диференціальним рівнянням в частинних похідних (ДРЧП) порядку k відносно невідомої функції а ліва частина цієї рівності – диференціальним оператором з частинними похідними порядку k (тут зауважимо, що ).

Для кожного ДРЧП задається деяка область G зміни аргументів .

Означення 2. Визначена в області G задана рівнянням (1.1) дійсна функція , неперервна разом зі своїми частинними похідними, які входять в це рівняння і перетворюють його при відповідних підстановках в тотожність, називають регулярним розв’язком.

Поряд з регулярними розв’язками в теорії ДРЧП існують розв’язки, які перестали бути регулярними в деяких точках області G чи на многовидах. Це – так звані елементарні чи фундаментальні (сингулярні) розв’язки.

Лінійні ДРЧП 2-го порядку можна записати в такому вигляді:

(1.2)

де - диференціальний оператор; a_ij – коефіцієнти рівняння (сталі числа чи функції від змінних х, у).

Тут використано позначення:

і т.д.

В залежності від знаку виразу кожне з таких рівнянь має в точці наступний тип:

1. еліптичний, якщо ,

2. параболічний, якщо ,

3. гіперболічний, якщо .

Може бути так, що в різних точках області G чи її підобластях рівняння (1.2) може належати до різних типів. Кажуть, що таке рівняння є рівнянням змішаного типу.

Якщо в кожній точці даної області G рівняння (1.2) має один і той же тип, то його відносять до цього ж типу (еліптичного, параболічного чи гіперболічного).

Канонічні рівняння параболічного типу – рівняння теплопровідності, конвективної дифузії

Рівняння в частинних похідних параболічного типу описують нестаціонарні динамічні процеси, тобто такі, які змінюються в часі.

Найбільш типовими представниками рівнянь параболічного типу є:

Рівняння теплопровідності

В найбільш загальному, так званому, дивергентному вигляді в системі координат воно може бути представлене як

, (3.3)

де температура в точці в момент часу ; - питома теплоємність; - густина; - тензор (коефіцієнт) теплопровідності; - інтенсивність внутрішніх джерел тепла.

Тут так званий градієнт температури-вектор, в напрямку якого відбувається найшвидше її зростання (зміна);

- дивергенція (розходження) вектора .

В одновимірному випадку рівняння (3.3) має вид

, (3.4)

а для однорідного ізотопного матеріалу при лінійному поширенні тепла

, (3.5)

де - так званий коефіцієнт температуропроводності.

3.2.2. Рівняння конвективної дифузії мігруючих речовин в деякому пористому середовищі (наприклад, водорозчинних речовин в ґрунті) має вид:

, (3.6)

де - концентрація розчинених речовин в точці з координатами в момент часу ;

- вектор швидкості потоку (наприклад, фільтраційного); - коефіцієнт конвективної дифузії; - пористість середовища, - оператор Лапласа.

В різних математичних моделях коефіцієнт може означати:

1) коефіцієнт молекулярної дифузії, якщо (тобто при відсутності конвекції);

2) коефіцієнт конвективної дифузії при ;

3) коефіцієнт турбулентної дифузії – при наявності в потоці пульсацій (наприклад, в річці).

В одномірному випадку рівняння конвективної дифузії прийме вигляд:

, (3.7)

а рівняння молекулярної дифузії

(3.8)

Рівняння теплопровідності та дифузії за виглядом повністю аналогічні.

Крайові умови та їх види

Для всіх фізичних задач характерним є наявність меж розглядуваної області , в якій вивчається той чи інший процес. Ці межі можуть бути як скінченні, так і простягатись в нескінченність. Постільки та чи інша математична модель повинна по можливості адекватно описувати розглядуване фізичне явище в даному виділеному середовищі, вона мусить включати, крім самого диференціального рівняння (чи системи рівнянь) опису процесу, ще й додаткові умови. Ці додаткові умови дістали назву крайових умов. Під крайовими умовами розуміють сукупність граничних і початкових умов. Граничні умови задають режим фізичного процесу на межі розглядуваної області , а початкові – накладають умови на функцію та її похідні до -го порядку по часу в деякий початковий момент часу .

Задання граничних умов.

Граничні умови визначають режим фізичного процесу на межі області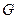

і можуть задаватись для всіх типів рівнянь в частинних похідних (якщо це потрібно).

В загальному випадку область задання рівняння можна представити як циліндр виду

де - фізична область – область зміни координат точок, що визначені процесом;

- проміжок часу, на якому вивчається процес (рис.3.1).

Типи граничних умов.

При описі граничних умов будемо розглядати їх математичну та фізичну інтерпретації:

а) граничні умови І-го роду

(3.10)

Тут - біжуча точка контору .

Математично:	Фізично:
На межі області задана функція	На межі області відома температура (концентрація, потенціал тощо).

б) граничні умови ІІ-го роду:

(3.11)

Тут - нормаль до межі - значення потоку.

Математично:	Фізично:
На межі області задана похідна функції	На межі області задано тепловий потік (потік концентрації і т.п.).

в) граничні умови 3 – го роду:

(3.12)

, причому .

Математично:	Фізично:
На межі області задана лінійна комбінація функцій та її похідної.	На межі області задано теплообмін з оточуючим середовищем, наприклад, по закону Ньютона-Ріхмана , де - коефіцієнт теплообміну, - температура оточуючого середовища.

г) граничні умови IV-го роду – це так звані умови спряження. Вони наявні для областей, що складаються не менше як з двох під областей, які характеризуються різними фізичними властивостями (рис.3.2). Наприклад, при дослідженні процесу теплопровідності розглядаються два стержні з різних матеріалів, які мають різні теплофізичні властивості (теплоємність, густину, коефіцієнт теплопровідності). В загальному можна сказати, що під області

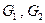характеризуються різними коефіцієнтами провідності.

При цьому межа контакту двох середовищ може розглядатись як:

а) ідеальною (рівність функцій і потоків);

б) неідеальною (скачок функцій і рівність потоків);

в) що має джерела і т.п. (рівність функцій і нерівність потоків).

Розглянемо, наприклад, умови спряження для ідеального та неідеального контактів:

а) ідеальний контакт

, (3.13)

б) у випадку неідеального контакту граничні умови повинні бути записані з врахуванням термічного опору контакту

(3.14)

Відмітимо, що також є інші види граничних умов, а саме граничні умови, які використовують при розв’язуванні задач з фазовими переходами. Такі задачі виникають при вивченні процесів кристалізації, промерзання, плавлення, горіння та інших і називають задачами Стефана.

3.4.Постановка крайових задач для рівнянь
еліптичного типу

Із сказаного вище робимо висновок про те, що всяку крайову задачу можна представити у наступній наглядній формі:

Продемонструємо постановки крайових задач, які можуть ставитись для рівняння Лапласа.

1. Перша крайова задача (задача Діріхле):

(3.15)

Потрібно знайти двічі неперервно диференційовану функцію відповідно по і в області , неперервну в замкнутій області , яка задовольняє рівняння Лапласа в області і приймає задані значення на її межі .

2. Друга крайова задача (задача Неймана):

(3.16)

Потрібно знайти двічі неперервно диференційовану функцію в обл. , неперервну в замкнутій області , яка задовольняє рівняння Лапласа в області , на межі якої задана похідна по нормалі до границі області цієї функції.

3. Третя крайова задача:

(3.17)

де , такі, що .

Потрібно знайти двічі неперервно диференційовану функцію , яка задовольняє рівняння Лапласа в області , неперервну в замкнутій області , на межі якої задана гранична умова третього роду.

4. Змішана задача теорії потенціалу (Діріхле-Неймана)

Розглядається крайова задача для рівняння Лапласа в області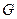

, на межі якої задаються почергово крайові умови першого та другого роду (рис. 3.3);

(3.18)

В такій постановці задається, наприклад, задача плоскої встановленої фільтрації підземних вод.

Продемонстровані вище постановки крайових задач називають класичними. Існують і інші постановки задач (в тому числі і некласичні).

Початкова крайова задача для рівняння Лапласа, як показав Адамар (див., наприклад, [2 б]), є некоректною.

Аналогічні крайові задачі ставляться для рівняння Пуассона та багатьох інших еліптичних рівнянь.

3.5. Постановка крайових задач для рівнянь
параболічного типу

Дані постановки проілюструємо на прикладі одномірного рівняння теплопровідності (3.5).

1. Задача Коші:

(3.19)

Потрібно знайти функцію , двічі неперервно диференційовану по і диференційовану по , яка задовольняє на всій осі рівнянню теплопровідності і при початковій умові .

2. Змішана крайова задача:

(3.20)

Потрібно знайти функцію , двічі неперервно диференційовану по і диференційовану по , яка задовольняє даному диференціальному рівнянню, початковій умові (при ), а на кінцях відрізка приймає задані значення - і .

Це приклад змішаної крайової задачі з граничними умовами першого роду. Можуть ставитись змішані крайові задачі з граничними умовами інших родів.

Як приклад розглянемо ще постановку змішаної крайової задачі з умовами спряження. Вона моделює процес поширення тепла в стержні, що складається з двох (чи більше) різних за теплофізичними властивостями матеріалів (рис. 3,4).

(3.21)

Тут

- теплопровідності матеріалів; - точка ідеального контакту матеріалів. Дві останні умови якраз і задають додаткові умови в точці контакту.

Слід відмітити, що для рівнянь параболічного типу можуть ставитись також задачі без початкових умов (див. [13 б]). Це означає, що фізичні процеси, змодельовані даними крайовими задачами, почалися дуже давно (при ) і продовжуються надто довго ( ).

Лабораторна робота №1.

Тема: Чисельне роз’язування крайової задачі Діріхле для рівняння Лапласа.

Мета. Отримати різницеву схему крайової задачі Діріхле для рівняння Лапласа та навчитись її розв’язувати ітераційним методом Гаусса-Зейделя.

Завдання. Провести чисельний розрахунок стаціонарного розподілу температури внутрішніх точках пластини, який описується рівнянням Лапласа в області G .

і задовільняють граничним умовам

Розрахунки проводити з точністю . Область G має вигляд:

Граничні умови такі :

коли ;

коли ,

де

n – номер варіанту, h =1 – крок сітки,

- число букв прізвища.

- число букв імені студента по паспорту, помножене на 30.

Порядок виконання роботи.

1. Вивчити постановку задачі про стаціонарне поширення тепла в плоскій пластині та записати її математичну модель в диференціальній формі.

2. Записати різницеву схему даної задачі.

3. Користуючись алгоритмом ручного рахунку (див. вище ) провести чисельний розрахунок розподілу температури ітераційним методом з усередненням Лібмана з точністю .

4. Скласти блок-схему алгоритму та відповідну програму для ПЕОМ розрахунку температури.

5. Провести розрахунки на ПЕОМ з точністю до .

6. Порівняти результати ручного і машинного рахунків. Зробити висновок.

7. Оформити та захистити лабораторну роботу.

Контрольні запитання.

1. Навести приклади основних рівнянь математичної фізики та їх типових представників; фізичні процеси, які вони описують.

2. Поняття крайової задачі. Типи граничних умов, їх математичний та фізичний зміст.

3. Постановка крайових задач для рівнянь еліптичного типу (на прикладі рівнянь Лапласа та Пуассона).

4. Суть принципу максимуму для рівнянь еліптичного типу при виборі початкового наближення.

5. Методи розв’язування крайових задач для рівнянь еліптичного типу.

6. Апроксимація похідних.

7. Різницева схема крайової задачі Діріхле для рівнянь Лапласа і Пуассона.

8. Чисельні методи розв’язування різницевих схем.

9. В чому переваги методу послідовної верхньої релаксації над ітераційним методом Якобі і Гаусса-Зейделя?

Явна різницева схема

Апроксимуючи похідні по формулах (6), (7) і підставляючи їх в рівняння (2) отримаємо

(9)

Шаблон явної різницевої схеми має вигляд (Рис.1).

З формули (9) легко визначити

(10)-(12) – це явна різницева схема для змішаної краєвої задачі теплопровідності з крайовими умовами І-го роду. Дана різницева схема явна, бо температура на k +1 шарі визначається явно із системи рівнянь.

В література доведено, що така явна різницева схема є стійкою, якщо параметр

(14)

Це означає, що при числовому розв’язку даної задачі по явній схемі кроки сітки h і не можна вибирати довільними, а з врахуванням умови стійкості (14) даної різницевої схеми.

Таким чином недолік явної різницевої схеми полягає в жорізнецева схематкій умові стійкості, а саме в тому, що кроки h і зв’язані. Якщо зафіксувати один з них, то другий потрібно вибирати з умови стійкості.

Приклад:

При машинних розрахунках зручно покласти 0,5 або .

Таким чином матимемо:

(15)

(16)

Доведено, що похибка явної різницевої схеми (10)-(12) при =0,5 або = наступна

при наявності джерел в (10) потрібно добавляти .

Алгоритм ручного рахунку

1. Обчислити коефіцієнт температуропроводності .

2. Вибрати число поділу відрізка .

3. Обчислити розбиття відрізка .

4. Користуючись умовою стійкості (14) обчислити крок по поклавши .

5. При заданому обчислити кількість кроків по часу .

6. Покрити область прямокутною сіткою з кроками h і .

7. Користуючись початковою умовою обчислити (обчислити температуру на нижній основі прямокутної області).

8. Використовуючи граничні умови обчислити , де - температура на лівій межі, а - температура на правій межі.

9. Використовуючи MS Excel обчислити по явній різницевій схемі по функції (15) чи (16).

10. Обчислити розподіл температури у вузлах сітки.

Результати числових розрахунків занести в таблицю. Побудувати сімейство графіків.

Приклад:

Неявна різницева схема.

Розглянемо неявну різницеву схему для І-ї краєвої задачі для рівняння теплопровідності.

Як вже зазначалося, явна різницева схема досить проста для розуміння, але володіє істотними недоліками і при чисельних розрахунках прикладних задач спеціалістами в даний час майже не використовується.

По відношенню до стійкості, явну різницеву схему називають умовно стійкою, оскільки вона стійка при певному обмеженні на відношення просторово-часових кроків h і а саме: де В той же час неявні різницеві схеми вільні від таких недоліків.

Як вже відмічалось раніше, неявну різницеву схему отримують шляхом апроксимації (заміни) похідної лівостороньою скінченою різницею по відношенню до вузла ( ), де апроксимують тільки на шарі, тобто шаблон неявної різницевої схеми має вигляд літери “Т” (рис.2.). Отже, після апроксимації похідних , і підставляючи їх в рівняння теплопровідності (2), апроксимуючи початкові і граничні умови (4) отримаємо неявну різницеву схему

Виявляється, що дана неявна різницева схема є стійкою при будь-яких кроках h і і називається абсолютно стійкою. Порядок її апроксимації , тобто перший по і другий – по h. Розв’язок даної схеми знаходиться послідовним обчисленням температури на часових шарах, починаючи з першого ( ). При цьому розв’язок на кожному шарі знаходять методом прогонки, який є однією з модифікацій методу Гаусса розв’язування системи лінійних алгебраїчних рівнянь. В (17) невідомою є температура на шарі, і відомою на -му шарі. Для цього приведемо схему (19) до так званого прогоночного виду:

де ,

Згідно цього методу розв’язок даної різницевої схеми пов’язано з розв’язком СЛАР і набагато важчий ніж розв’язок явної різницевої схеми, але якщо розглянути (20) неважко показати, що матриця буде трьох діагональною. І розв’язок будемо шукати у вигляді

. (22)

Різницева схема (20)-(21) називається неявною різницевою схемою. Розглянемо спеціальні методи розв’язання систем з трьох діагональною матрицею. Цей метод називається методом прогонки. Тут - прогоночні коефіцієнти обчислені на часовому шарі .

Справа в тому, що на кожному часовому шарі приходиться виконувати свою прогонку, тобто розв’язувати СЛАР на кожному шарі по часу. Підставивши (22) в (20), отримаємо:

звідси отримаємо

Остання рівність можлива лише в тому випадку, коли

Звідки знаходимо прогоночні коефіцієнти

, (23)

Щоб обчислити значення про гоночних коефіцієнтів користуючись формулами (23), потрібно мати значення коефіцієнтів , які легко знаходяться із граничних умов (21). Використовуючи (22) і (21) маємо

Таким чином розв’язок неявної різницевої схеми (20)-(21) використовує метод прогонки і він дає формули (22), (23), (25). Для інших краєвид задач розв’язок дається формулами (22), (23), але інші. Тобто маємо

(7.22)

Вони обчислюються в результаті прямого ходу (прямої прогонки). В результаті зворотного ходу (зворотної прогонки), обчислюємо по формулі (22) в кожній точці стержня на даному часовому шарі (в певний момент часу).

Зауваження І. На кінцях стержня можуть задаватися різні граничні умови (І-ІІІ роду).

В зв’язку з цим неявна різницева схема (20) – (22) в більш загальному вигляді запишеться так:

де коефіцієнти ₁, ₂, , визначаються тим чи іншим чином в залежності від задання граничних умов І роду, коли задано розподіл температури на кінцях стержня

маємо

для граничних умов ІІ роду, коли на кінцях стержня задано теплові потоки,

(28)

маємо

Якщо співставити (27) і (28), то про гоночні коефіцієнти

(30)

Ці формули справедливі для задання будь-яких граничних умов.

для граничних умов ІІІ роду, тобто коли наявний теплообмін між стержнем і навколишнім середовищем

де - температура оточуючого середовища, маємо

(31)

Прогоночні коефіцієнти для всіх випадків граничних умов, обчислюються за формулами (23), причому

(7.23)

У випадку задання граничної умови ІІ або ІІІ роду на правому кінці стержня для проведення прогонки по формулах (22) потрібно знайти температуру . З формул (22) і (20), (27) маємо

Звідки знаходимо :

(32)

Зауваження 2. Для можливості застосування методу прогонки, достатньо, щоб виконувались умови

7.2.1 Алгоритм ручного рахунку по неявній різницевій схемі.

1. Обчислити коефіцієнт температуропровідності

2. Вибрати число поділу відрізка .

3. Обчислити крок розбиття відрізка

4. Вибрати крок по часу та їх кількість m.

5. Обчислити коефіцієнт

6. Покрити область різницевою сіткою з кроками h і .

7. Користуючись початковою умовою, обчислити

8. Користуючись граничними умовами, обчислити

9. Записати неявну різницеву схему задачі.

10. Для кожного часового шару

а) в результаті прямого ходу, обчислити поргоночні коефіцієнти

б) в результаті зворотного ходу, обчислити значення температури

Приклад: Розрахунок розподілу температури в стержні за допомогою неявної різницевої схеми.

Розглянемо умову задачі прикладу 2 поширення тепла в стержні.

Згідно умови, маємо

Виберемо крок по часу, наприклад, таким же, як і при застосуванні явної схеми (з метою порівняння результатів по обох різницевих схемах): c.

Обчислення температури будемо проводити для трьох часових шарів (m=3). Параметр , як і раніше, обчислюється так

Початкова і граничні умови такі ж, як і раніше.

Для кожного часового шару k (k=1,2,3) обчислюємо в результаті прямого ходу прогоночні коефіціенти (користуючись формулами (23)), а в результаті зворотного ходу–температуру . Відповідно маємо:

а) для першого часового шару (k=1)

і
1	0	1000	969,017
2	0,12500	857,000	896,14
3	0,12698	797,587	776,13
4	0,12702	698,792	609,01
5	0,12702	558,210	400

Табл. Температура першого часового шару для стержня

б) для другого часового шару (k=2)

i
1	0	1000	962,83
2	0,12500	851,762	888,52
3	0,12698	790,933	788,52
4	0,12702	691,946	602,82
5	0,12702	552,015	400

Табл. Температура другого часового шару для стержня

в) для третього часового шару (k=3)

i
1	0	1000	957,26
2	0,12500	847,115	881,19
3	0,12698	784,538	761,19
4	0,12702	685,335	597,26
5	0,12702	546,457	400

Табл. Температура третього часового шару для стержня.

Обчислені значення температур для кожного часового шару запишемо для наглядності у зведену таблицю.

i j		0	1	2	3	4	5
i j		0	0,02	0,04	0,06	0,08	0,1
0	0	1000	976	904	784	616	400
1	1 t	1000	969,017	896,14	776,13	609,01	400
2	2 t	1000	962,82	888,52	768,52	602,82	400
3	3 t	1000	957,26	881,19	761,19	597,26	400

Табл. Зведена таблиця розподілу температур у стержні.

Лабораторна робота №2

Тема. Чисельне розв’язання змішаної крайової задачі для рівняння теплопровідності.

Мета. Навчитись проводити розрахунок поширення тепла по явній та неявній різницевих схемах у випадку першої крайової задачі для рівняння теплопровідності.

Завдання. Розрахувати розподіл температури в однорідному стержні довжини l, виготовленого з певного матеріалу з теплофізичними властивостями l,c,r , температура T(x,t) в якому задовольняє рівнянню теплопровідності

a² ,0 < х<l, 0<t<t₁,

якщо крайові умови мають вид:

відомо розподіл температури в початковий момент часу

T ( x ,0)= f ( x )= x ^s ⁺¹ + T ₁ ,

і теплові режими (підтримується задана температура) на кінцях стержня

Т(0,t)= (t) =T₁=k,

T(l,t)=

де k – номер варіанта, S–номер групи.

Для розрахунків взяти l=0,5м, h =0,1м , m=3.

Порядок виконання роботи.

1. Записати математичну модель процесу поширення тепла в однорідному стержні довжини l в диференціальній формі.

2. Записати явну різницеву схему крайової задачі.

3. По таблиці теплофізичних величин виписати для свого варіанту.

4. Користуючись приведеним вище алгоритмом ручного рахунку, виконати розрахунок розподілу температури в стержні по явні схемі.

5. Результати рахунку занести в таблицю.

6. Побудувати графіки залежностей T=T(x, t_*), T=T(x_*, t), t_*, x_*–параметри.

7. Провести розрахунок по явній схемі на ПЕОМ.

8. Виконати розрахунок розподілу температури, користуючись вище – приведеним алгоритмом ручного рахунку, по неявній різницевій схемі.

9. Результати обчислень прямого і зворотнього ходів занести в таблиці, аналогічні таблицям 4–6. Значення температури для кожного температурного шару виписати у зведену таблицю 7.

10. Побудувати графіки залежностей розподілу температури

T=T(x, t_*), T=T(x_*, t).

11. Провести розрахунок по неявній схемі з використанням ПЕОМ.

12. Порівняти окремо для кожної схеми результати ручного рахунку і машинного. Зробити висновки.

13. Оформити і захистити лабораторну роботу.

Контрольні запитання.

1. Навести приклади основних рівнянь математичної фізики та їх типових представників; вказати фізичні процеси, які вони описують.

2. Поняття крайової задачі. Крайові умови; типи граничних умов.

3. Постановки крайових задач для рівнянь параболічного типу (наприклад, одновимірного рівняння теплопровідності ).

4. Принцип максимуму для рівнянь параболічного типу.

5. Методи розв’язування крайових задач для рівнянь параболічного типу.

6. Апроксимація похідних.

7. Явна різницева схема першої крайової задачі для найпростішого рівняння теплопровідності та її розв’язування.

8. Критерій стійкості явної схеми.

9. Недоліки явної різницевої схеми.

10. Неявна різницева схема першої крайової задачі для найпростішого рівняння теплопровідності та її переваги.

Суть методу прогонки розв’язування неявної різницевої схеми.

Деякі позначення

Вступ

Нехай задано рівняння параболічного типу, що містить першу похідну:

(1)

З фізичної точки зору дане рівняння описує процес, що характеризує дифузійно-конвективний перенос деякої матеріальної субстанції. Приклад: масоперенос, теплоперенос. Перший член відповідає за перенос дифузійним шляхом (коефіцієнт дифузфї рівний одиниці), а другий відповідає за перенос конвективним шляхом.

Рівняння масопереносу: (2)

С-концентрація речовин.

Особливістю числового розв’язку крайових задач для рівнянь (1), або (2) є наявність члена з першою похідною, або конвективного числа.

Ми апроксимуємо цей конвективний член кількома способами:

(3)

Перший спосіб веде до нестійкої схеми. Третій спосіб веде до “помітних викидів” числового розв’язку. Тому даний член апроксимується лівосторонньою різницею (протипотоковою).

Однак при апроксимації конвективного члена лівосторонньою різницею при використанні звичайної неявної різницевої схеми при деяких h і τ спостерігаються осциляції чисельного розв’язку. Тому різницева схема в якій спостерігаються осциляції чисельного розв’язку є монотонною.

Різницеві схеми, що зберігають монотонність розв’язку різницевих задач називаються монотонними (чисельний розв’язок не має осциляції). Отримані раніше розв’язки по явній різницевій схемі були монотонними.

Вступ. Методи побудови РС

В основному склалося три основні способи побудови РС на заданому шаблоні :

1.Метод різницевої апроксимації (той, що ми розлядали до сих пір) ;

2.Метод невизначених коефіцієнтів;

3.Інтегро-інтерпаляційний метод (метод балансу);

1. Метод різницевої апроксимації полягає в тому, що кожна похідна, що входить в диференціальне рівняння і крайові умови змінюється певним різницевим виразом (включаючи лише вузли шаблону). Саме так були отримані всі розглянуті нами вище різницеві схеми. Цей метод досить простий і додаткових пояснень не потребує.

Метод різницевої апроксимації дозволяє легко складати РС першого чи другого порядку апроксимації на прямокутній сітці для рівнянь з неперервними і достатньо гладкими коефіцієнтами. Однак цей метод важко чи неможливо застосувати в більш складних випадках , а саме для рівнянь з розривними коефіцієнтами, на прямокутних сітках , для рівнянь високого порядку , на нерівномірних сітках і т. д.

Приклад: маємо стержень, що складається з неоднорідного матеріалу(половина сталь, половина мідь).

c1,ρ1,λ1 c2, 2 ρ,λ2

ℓ* ℓ

2. Метод невизначених коефіцієнтів полягає в тому , що в якості РС беруть лінійну комбінацію значень різницевого розв’язку у вузлах шаблону. Коефіцієнти цієї лінійної комбінації вимагають умови, щоб нев’язка схема мала як можна більш високий порядок малості відносно t і h.

Завдання: методом невизначених коефіцієнтів побудувати РС кривої задачі Діріхле для рівняння Пуассона чи Лапласа в прямокутній області на рядку точності 0(h ).

3.Інтегро-інтерпаляційний метод, один з варіантів якого називається методом балансу. Він найбільш надійний і застосовується а всіх випадках. В цьому методі після вибору шаблону область G розбивається на комірки певним чином зв’язаних з шаблоном.

Диференціальне рівняння інтегрують по комірці і використовуючи формули векторного аналізу, приводять до інтегральної форми, що відповідає фізичному закону збереження. Наближено обчислюючи отримані інтеграли, за "квадратурними формулами, складають РС.

Інтегро-інтерполяційний метод особливо корисний для рівнянь з негладкими, або розривними коефіцієнтами. Оскільки саме інтегральний метод запису законів збереження виділяє із всіх математично-допустимих розв’язків, таких рівнянь, фізично правильний узагальнений розв’язок. При побудові РС інтегро-інтерполяційним методом, застосовують методи інтерполяції інтегрального співвідношення, записаного відносно елементарної комірки сітки. Змінюючи інтерполяцію шуканого розв’язку і коефіцієнтів рівняння, можна отримати різні інтерполяційні схеми.

ІІМ дозволяє будувати однорідні РС на скрізному рахунку, тобто такі РС, коефіцієнти яких обчислюється у всіх вузлах довільної сітки для будь-якої задачі із даного класу за одними і тими ж формулами . Це особливо важливо при розгляді крайових задач із розривними коефіцієнтами і таких крайових задач , в яких нерегулярність РС має різницеве походження, наприклад, за рахунок апроксимації розв’язку в граничних точках.

РС, що виражають на сітці закони збереження називаються консервативними схемами. Крім того , при побудові РС повинні виконуватись не лише різницеві аналоги основних законів збереження, але й всі співвідношення, які диктуються фізичними законами даної задачі. В цьому випадку схеми називаються повністю консервативними. Повністю консервативні РС дозволяють вести розрахунки на порівняно грубих сітках .

Сумарна апроксимація

Принцип сумарної апроксимації полягає в наступному: кожне з рівнянь (0)-(1) апроксимує вихідне диференціальне рівняння (1) з першого пункту (РС звагами для двохвимірного рівняння ) з точністю 0(t+h²). При переході з цілого шару k на шар k+½ кожна просторова різниця обчислюється несеметрично по часу і похибка апроксимації кожної з РС рівна 0(τ+h²). Але похибка на другій половині шару по часу компенсує першу і в сумі при переході з цілого шару k на k+1 , тоді похибка має такий порядок апроксимації ). Математично це має такий вигляд :

***Схема стійка при будь-яких кроках і h. Схему змінніх напрямків можна досліджувати двояко

1) виключивши з різницевих рівнянь;

2) безпосередньо шляхом сумарної апроксимації

Нехай U(x t)-точний розв’язок . Представимо розв’язок різницевої задачі у вигляді:

(26)

де -це нев’язка, тобто різниця між точним і наближеним розв’язком.

(27)

Підставляючи вказані вирази (26), (27) в (10), (11) отримаєм рівняння, які задовольняють похибки методу:

Ці сіткові функції називаються похибками апроксимації різницевої задачі (10)-(11) на розв’язок вихідної задачі (1)-(3).

Розкладаючи функції, які входять в дані вирази по формулі Тейлора в околі точки отримаємо:

Із (28) видно, що кожне з різницевих рівнянь (10)-(11) апроксимує вихідне рівняння з першим порядком по і другим порядком по h, де ,

сумарна апроксимація (28)

Разом з тим, сума похибок апроксимації має другий порядок має другий порядок по і другий порядком по h. Знаходимо сумарну похибку:

(30)

(31) (32)

Кажуть, що схема (10)-(11) володіє сумарною апроксимацією другого порядкупо і другого порядку по h.

Вступ

Поряд з розглянутими різними методами чис. розв’язку крайових задач математичної фізики існують і інші методи . Одним із них є варіаційні і проекційні методи, які зайняли в обчислювальній математиці досить важливе місце. Особливо ефективні вони в тих задачах, де шуканими є функціонали від розв’язку. Виявилось, що уже при порівняно невеликих наближеннях функціонали отримали з великою точністю. Найбільш повне теоретичне обґрунтування методів-С. Г. Міхліна, який встановив необхідність і достатність умови стійкості варіац. методів в просторах з енергетичною нормою.

Активний розвиток варіаційних методів показав і деякі їх недоліки пов’язані з трудністю побудови базисних функцій. Новий напрямок в розвитку варіаційних і проекційних методів при застосуванні їх до крайових задач крайових задач математичної фізики було розвинуто при застосуванні базисних функцій спеціальної конструкції , а саме, які відмінні від нуля в деяких порівняно невеликих областях. Перші роботи по цьому напрямку належать вченим Куран , Оганасян , Ліонс , Обен , Біргоф, Варга , і т. д. Далі ці роботи продовжені в роботах Бабушки , Стренг і Фікс , Зламал Дуглас, Шайдуров і т. д. В різницевих методах в ряді випадків є доцільним отримувати наближений розв’язок з заданою точністю за рахунок формального збільшення розмірності півпросторів (Наприклад, зменшення кроку сітки). Інший спосіб – за рахунок побудови більш точних апроксимацій вихідної задачі на основі апріорної інформації про гладкість розв’язку. Така точка зору виявилась дуже корисною і привела дослідників до досить зручних і універсальних методів побудови різницевих рівнянь на основі варіаційних методів Рітца, Гальоркіна і методу найменших квадратів.

Метод скінчених елементів (МСЕ) в даний час є одним із самих поширених методів розв’язування прикладних задач (вивчення теплових процесів , проблем динаміки рідини, розрахунків напруженого деформов. стану конструкції і т. д.). Спочатку МСЕ був запропонований інженерами. Знайшов широке застосування на практиці , але довгий час залишався поза увагою математиків. Після достатнього його дослідження математиками виявилось, що при негладких вхідних даних задачі МСЕ часто сходиться швидше, ніж метод скінчених різниць, а інколи взагалі володіє оптимальною швидкістю збіжності. МСЕ для розв’язання крайових задач суцільних серед. Вперше був застосований в середині 50-х рр. ⅩⅩ ст.. і з тих часів завоював відомість виключно корисного інженерного методу. Його основою є варіаційне числення. Диференціальні рівняння, що описують крайову задачу та відповідні крайові умови використовується для постановки варіаційної задачі, яка потім розв’язується безпосередньо. З цієї точки зору МСЕ являє собою неявне застосування методу Ріцца на окремих відрізках. ВМСЕ фізична задача замінюється кусково-гладкою моделлю.

Основна концепція МСЕ

Основна ідея МСЕ полягає в тому, що довільну шукану неперервну функцію φ(t˚, тиск, переміщення, потенціал і т. д.) можна апроксимувати дискретною моделлю, яка будується на множині кусково-неперервної функції, визначеної на скінченому числі підобластей.

Кусково - неперервні функції визначаються за допомогою значень неперервної величини в скінченному місці точок розглядуваної області. В загальному випадку неперервна величина наперед невідома і потрібно визначити значення цієї величини в деяких внутрішніх точках області. При побудові дискретної моделі поступимо наступним чином:

1.В розглядуваній області Ω фіксують скінчене число точок . Ці точки називаються вузловими або просто вузлами (дискретизація області)

і®Ui

2.Значення шуканої наперед функції φ в кожній вузловій точці вважається змінною, яка може бути визначена.

3.Область визначення неперервної величини φ розбивається на скінчене число підобластей, яке називається елементарними . Ці елементи мають загальні вузлові точки , не перекриваються і в сукупності апроксимують форму області (розбиття тіла чи області на скінченні елементи).

4.Неперервна величина φ апроксимується на кожному елементі поліномом, який визначається за допомогою вузлових значень цієї величини. Для кожного елемента визначається свій поліном , але поліном вибирається таким чином , щоб зберігалась неперервність величини вздовж меж елемента (вибір схеми інтерпаляції функції в середині елемента ).

5. Виведення рівнянь для схеми в цілому.

6.Ров’язування системи рівнянь.

7.Обчислення значень інших величин.

Переваги і недоліки МСЕ

В даний час область застосування МСЕ дуже широка і охвачує всі фізичні задачі, що можуть бути описані дифрівняннями.

Найбільш важливі переваги методу МСЕ наступні:

1) Застосування методу до розв’язання крайових задач, що складаються з підобластей з різними фізичними властивостями.

2) Застосування методу до підобластей з криволінійними межами.

3) Розміри елемента можуть бути змінними, це дозволяє укрупнювати чи подрібнбвати сітку розбиття області на елементи, якщо в цьому є необхідність.

4) Вхідні дані задачі можуть бути негладкими. Крайові умови задачі можуть бути розривними.

5) При складанні програми для певного класу задач за допомогою МСЕ можна вирішувати будь-яку задачу з цього класу.

Головний недолік МСЕ в складності програми і застосуванні потужної обчислювальної техніки.