Рівняння теплопровідності

В найбільш загальному, так званому, дивергентному вигляді в системі координат  воно може бути представлене як

,                                  (3.3)

де  температура в точці  в момент часу ;  - питома теплоємність;  - густина;  - тензор (коефіцієнт) теплопровідності;  - інтенсивність внутрішніх джерел тепла.

Тут  так званий градієнт температури-вектор, в напрямку якого відбувається найшвидше її зростання (зміна);

- дивергенція (розходження) вектора .

В одновимірному випадку рівняння (3.3) має вид

,                                      (3.4)

а для однорідного ізотопного матеріалу при лінійному поширенні тепла

,                                                          (3.5)

де   - так званий коефіцієнт температуропроводності.

 

3.2.2. Рівняння конвективної дифузії мігруючих речовин в деякому пористому середовищі (наприклад, водорозчинних речовин в ґрунті) має вид:

,                                                  (3.6)

де  - концентрація розчинених речовин в точці з координатами  в момент часу ;

- вектор швидкості потоку (наприклад, фільтраційного);       - коефіцієнт конвективної дифузії;   - пористість середовища,   - оператор Лапласа.

В різних математичних моделях коефіцієнт  може означати:

1) коефіцієнт молекулярної дифузії, якщо   (тобто при відсутності конвекції);

2) коефіцієнт конвективної дифузії при ;

3) коефіцієнт турбулентної дифузії – при наявності в потоці пульсацій (наприклад, в річці).

В одномірному випадку рівняння конвективної дифузії прийме вигляд:

,                                      (3.7)

а рівняння молекулярної дифузії 

                                                       (3.8)

Рівняння теплопровідності та дифузії за виглядом повністю аналогічні.

 

Крайові умови та їх види

Для всіх фізичних задач характерним є наявність меж розглядуваної області , в якій вивчається той чи інший процес. Ці межі можуть бути як скінченні, так і простягатись в нескінченність. Постільки та чи інша математична модель повинна по можливості адекватно описувати розглядуване фізичне явище в даному виділеному середовищі, вона мусить включати, крім самого диференціального рівняння (чи системи рівнянь) опису процесу, ще й додаткові умови. Ці додаткові умови дістали назву крайових умов. Під крайовими умовами розуміють сукупність граничних і початкових умов. Граничні умови задають режим фізичного процесу на межі  розглядуваної області , а початкові – накладають умови на функцію  та її похідні до -го порядку по часу в деякий початковий момент часу .

 

Задання початкової умови (для рівнянь параболічного типу – теплопровідності та дифузії)

 

Оскільки в розглядуваних вище рівняннях параболічного типу входить лише перша похідна по часу, тобто , то згідно теоретичних досліджень слід задавати умови тільки на похідну нульового порядку, тобто саму функцію:

,                                                  (3.9)

де  - біжуча точка області .

Задання граничних умов.

 

Граничні умови визначають режим фізичного процесу на межі області 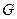 і можуть задаватись для всіх типів рівнянь в частинних похідних (якщо це потрібно).

В загальному випадку область задання рівняння можна представити як циліндр виду

де   - фізична область – область зміни координат точок, що визначені процесом;

- проміжок часу, на якому вивчається процес (рис.3.1).

 

Типи граничних умов.

При описі граничних умов будемо розглядати їх математичну та фізичну інтерпретації:

а) граничні умови І-го роду

                                            (3.10)

Тут   - біжуча точка контору .

 

Математично:	Фізично:
На межі  області  задана функція	На межі області відома температура (концентрація, потенціал тощо).

 

б) граничні умови ІІ-го роду:

                                                    (3.11)

Тут  - нормаль до межі   - значення потоку.

 

Математично:	Фізично:
На межі  області  задана похідна функції	На межі області задано тепловий потік (потік концентрації і т.п.).

 

в) граничні умови 3 – го роду:

                    (3.12)

,      причому .

 

Математично:	Фізично:
На межі області задана лінійна комбінація функцій та її похідної.	На межі області задано теплообмін з оточуючим середовищем, наприклад, по закону Ньютона-Ріхмана , де  - коефіцієнт теплообміну,  - температура оточуючого середовища.

 

г) граничні умови IV-го роду – це так звані умови спряження. Вони наявні для областей, що складаються не менше як з двох під областей, які характеризуються різними фізичними властивостями (рис.3.2). Наприклад, при дослідженні процесу теплопровідності розглядаються два стержні з різних матеріалів, які мають різні теплофізичні властивості (теплоємність, густину, коефіцієнт теплопровідності). В загальному можна сказати, що під області

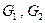 характеризуються різними коефіцієнтами провідності.

При цьому межа контакту двох середовищ може розглядатись як:

а) ідеальною (рівність функцій і потоків);

б) неідеальною (скачок функцій і рівність потоків);

в) що має джерела і т.п. (рівність функцій і нерівність потоків).

 

Розглянемо, наприклад, умови спряження для ідеального та неідеального контактів:

а) ідеальний контакт

,                          (3.13)

б) у випадку неідеального контакту граничні умови повинні бути записані з врахуванням термічного опору контакту

           (3.14)

Відмітимо, що також є інші види граничних умов, а саме граничні умови, які використовують при розв’язуванні задач з фазовими переходами. Такі задачі виникають при вивченні процесів кристалізації, промерзання, плавлення, горіння та інших і називають задачами Стефана.

 

3.4.Постановка крайових задач для рівнянь
еліптичного типу

 

Із сказаного вище робимо висновок про те, що всяку крайову задачу можна представити у наступній наглядній формі:

 

 

 

Продемонструємо постановки крайових задач, які можуть ставитись для рівняння Лапласа.

 

1. Перша крайова задача (задача Діріхле):

                        (3.15)

Потрібно знайти двічі неперервно диференційовану функцію  відповідно по  і  в області , неперервну в замкнутій області , яка задовольняє рівняння Лапласа в області  і приймає задані значення на її межі .

2. Друга крайова задача (задача Неймана):

                       (3.16)

Потрібно знайти двічі неперервно диференційовану функцію в обл. , неперервну в замкнутій області , яка задовольняє рівняння Лапласа в області , на межі якої задана похідна по нормалі  до границі  області  цієї функції.

3. Третя крайова задача:

               (3.17)

де , такі, що .

Потрібно знайти двічі неперервно диференційовану функцію , яка задовольняє рівняння Лапласа в області , неперервну в замкнутій області , на межі якої задана гранична умова третього роду.

4. Змішана задача теорії потенціалу (Діріхле-Неймана)

Розглядається крайова задача для рівняння Лапласа в області 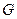, на межі якої задаються почергово крайові умови першого та другого роду (рис. 3.3);

                            (3.18)

 

В такій постановці задається, наприклад, задача плоскої встановленої фільтрації підземних вод.

Продемонстровані вище постановки крайових задач називають класичними. Існують і інші постановки задач (в тому числі і некласичні).

Початкова крайова задача для рівняння Лапласа, як показав Адамар (див., наприклад, [2 б]), є некоректною.

Аналогічні крайові задачі ставляться для рівняння Пуассона та багатьох інших еліптичних рівнянь.

 

3.5. Постановка крайових задач для рівнянь
параболічного типу

Дані постановки проілюструємо на прикладі одномірного рівняння теплопровідності (3.5).

1. Задача Коші:

                (3.19)

Потрібно знайти функцію , двічі неперервно диференційовану по  і диференційовану по , яка задовольняє на всій осі  рівнянню теплопровідності і при  початковій умові .

2. Змішана крайова задача:

               (3.20)

Потрібно знайти функцію , двічі неперервно диференційовану по  і диференційовану по , яка задовольняє даному диференціальному рівнянню, початковій умові (при ), а на кінцях відрізка  приймає задані значення -  і .

Це приклад змішаної крайової задачі з граничними умовами першого роду. Можуть ставитись змішані крайові задачі з граничними умовами інших родів.

Як приклад розглянемо ще постановку змішаної крайової задачі з умовами спряження. Вона моделює процес поширення тепла в стержні, що складається з двох (чи більше) різних за теплофізичними властивостями матеріалів (рис. 3,4).

 

            (3.21)

Тут

 - теплопровідності матеріалів;  - точка ідеального контакту матеріалів. Дві останні умови якраз і задають додаткові умови в точці контакту.

Слід відмітити, що для рівнянь параболічного типу можуть ставитись також задачі без початкових умов (див. [13 б]). Це означає, що фізичні процеси, змодельовані даними крайовими задачами, почалися дуже давно (при ) і продовжуються надто довго ( ).

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: