Компетенции обучающегося, формируемые в результате освоения дисциплины Стр 1 из 33Следующая ⇒ СОДЕРЖАНИЕ   ВВЕДЕНИЕ.. 4 Лабораторная работа 1-2. 6 ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ИНВЕСТИЦИОННЫХ РИСКОВ.. 6 Лабораторная работа 3-4. 25 ИМИТАЦИЯ В MS EXCEL С ИСПОЛЬЗОВАНИЕМ ИНСТРУМЕНТА.. 25 "ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ". 25 Лабораторная работа 5. 35 СТАТИСТИЧЕСКИЙ АНАЛИЗ РЕЗУЛЬТАТОВ ИМИТАЦИИ.. 35 Лабораторная работа 6-7. 42 ВВЕДЕНИЕ В СИСТЕМУ МОДЕЛИРОВАНИЯ VENSIM 5.0 PLE.. 42 Лабораторная работа 8. 58 МОДЕЛИРОВАНИЕ СИСТЕМ СРЕДСТВАМИ GPSS WORLD.. 58 Лабораторная работа 9-10. 79 МОДЕЛИРОВАНИЕ ОДНОКАНАЛЬНЫХ УСТРОЙСТВ.. 79 Лабораторная работа 11-12. 88 МОДЕЛИРОВАНИЕ МНОГОКАНАЛЬНЫХ УСТРОЙСТВ.. 88 Лабораторная работа 13-14. 105 МОДЕЛИРОВАНИЕ ЗНАЧЕНИЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ С ЗАДАННЫМ... 105 ЗАКОНОМ РАСПРЕДЕЛЕНИЯ И ОБРАБОТКА РЕЗУЛЬТАТОВ.. 105 МОДЕЛИРОВАНИЯ СРЕДСТВАМИ GPSS WORLD.. 105 Лабораторная работа 15-16. 113 РАЗРАБОТКА ИМИТАЦИОННОГО ПРОЕКТА.. 113 В СИСТЕМЕ GPSS WORLD.. 113 СПИСОК ЛИТЕРАТУРЫ... 150     ВВЕДЕНИЕ     Рыночная экономика с быстро меняющейся конъюнктурой требует от специалистов любого звена экономики своевременного принятия адекватных управленческих решений. Информатизация всех сфер национальной экономики, обусловила необходимость разработки электронного курса по имитационному моделированию экономических процессов, позволяющему вырабатывать такие решения с использованием компьютерной техники и технологии. Методические указания посвящены овладению умениями и навыками использования компьютерных средств и информационных технологий для эффективного решения основных задач организации управленческой и экономической деятельности. Методические указания предназначены для студентов, изучающих дисциплину «Имитационное моделирование экономических процессов». Целью изучения дисциплины «Имитационное моделирование экономических процессов» является формирование системного представления об имитационном моделировании экономических процессов. Задачами дисциплины являются: ‒ рассмотрение современных концепций построения моделирующих систем, ‒ всестороннее освещение подходов и способов применения имитационного моделирования в проектной экономической деятельности и новых инструментальных средств этой области.  В результате изучения дисциплины каждый студент должен иметь представление: ‒ о перспективах развития систем имитационного моделирования; ‒ о направлениях в области имитационного моделирования экономических процессов, различных подходах к построению имитационных моделей; ‒ о возможностях, преимуществах и недостатках различных сис­тем моделирования, используемых при решении различных экономических задач. знать: ‒ основные определения и базовые понятия, касающиеся теоретических основ имитационного моделирования, метод Монте-Карло; ‒ технологию создания, отладки и эксплуатацию моделей экономических систем с использованием CASE- технологий конструирования моделей «без программирования» - с помощью диалогового графического конструктора; ‒ модели основных систем массового обслуживания; ‒ состояние и тенденции развития программного обеспечения; ‒ технологический процесс подготовки и решения задач на ПЭВМ. уметь: ‒ разрабатывать алгоритмы для имитационного моделирования экономических задач; ‒ решать конкретные задачи по разработке имитационных моделей экономических систем; ‒ оформлять программную документацию; ‒ моделировать процессы массового обслуживания в экономических системах; ‒ рассчитывать показатели эффективности операций в экономических системах при их имитационном моделировании; ‒ осуществлять анализ результатов имитационного моделирования экономических процессов. Лабораторная работа 1-2 ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ИНВЕСТИЦИОННЫХ РИСКОВ Теоретическая часть Имитационное моделирование представляет собой серию численных экспериментов, призванных получить эмпирические оценки степени влияния различных факторов (исходных величин) на некоторые зависящие от них результаты (показатели). В общем случае, проведение имитационного эксперимента можно разбить на следующие этапы. 1. Установить взаимосвязи между исходными и выходными показателями в виде математического уравнения или неравенства. 2. Задать законы распределения вероятностей для ключевых параметров модели. 3. Провести компьютерную имитацию значений ключевых параметров модели. 4. Рассчитать основные характеристики распределений исходных и выходных показателей. 5. Провести анализ полученных результатов и принять решение. Результаты имитационного эксперимента могут быть дополнены статистическим анализом, а также использоваться для построения прогнозных моделей и сценариев. Пример 1 Фирма рассматривает инвестиционный проект по производству продукта "А". В процессе предварительного анализа экспертами были выявлены три ключевых параметра проекта и определены возможные границы их изменений (табл. 1). Прочие параметры проекта считаются постоянными величинами (табл. 2).   Таблица 1 - Ключевые параметры проекта по производству продукта "А" Сценарий	Показатели
Наихудший	Наилучший	Вероятный
Объем выпуска – Q	150	300	200
Цена за штуку – P	40	55	50
Переменные затраты – V	35	25	30

 

Таблица 2 - Неизменяемые параметры проекта по производству продукта "А"

Показатели	Наиболее вероятное значение
Постоянные затраты – F	500
Амортизация – A	100
Налог на прибыль – T	60%
Норма дисконта – r	10%
Срок проекта – n	5
Начальные инвестиции – I0	2000

 

Первым этапом анализа согласно сформулированному выше алгоритму является определение зависимости результирующего показателя от исходных. При этом в качестве результирующего показателя обычно выступает один из критериев эффективности: NPV, IRR, PI .

Предположим, что используемым критерием является чистая современная стоимость проекта NPV:

,                                                                                       (1)

где NCF_t – величина чистого потока платежей в периоде t.

По условиям примера, значения нормы дисконта r и первоначального объема инвестиций I₀ известны и считаются постоянными в течение срока реализации проекта (табл. 2).

По условиям примера, ключевыми варьируемыми параметрами являются: переменные расходы V, объем выпуска Q и цена P. Диапазоны возможных изменений варьируемых показателей приведены в табл. 1. При этом будем исходить из предположения, что все ключевые переменные имеют равномерное распределение вероятностей.

Реализация третьего этапа может быть осуществлена только с применением ЭВМ, оснащенной специальными программными средствами. Поэтому прежде чем приступить к третьему этапу – имитационному эксперименту, познакомимся с соответствующими средствами ППП EXCEL, автоматизирующими его проведение.

Задания к лабораторному занятию

Базовый уровень

Упражнение 1.

Проведение имитационных экспериментов в среде ППП EXCEL можно осуществить двумя способами – с помощью встроенных функций и путем использования инструмента Генератор случайных чисел дополнения Анализ данных (Analysis ToolPack). Для сравнения ниже рассматриваются оба способа. При этом основное внимание уделено технологии проведения имитационных экспериментов и последующего анализа результатов с использованием инструмента Генератор случайных чисел.

Следует отметить, что применение встроенных функций целесообразно лишь в том случае, когда вероятности реализации всех значений случайной величины считаются одинаковыми. Тогда для имитации значений требуемой переменной можно воспользоваться математическими функциями СЛЧИС() или СЛУЧМЕЖДУ(). Форматы функций приведены в таблице 3.

Таблица 3 – Математические функции для генерации случайных чисел

Наименование функции

Формат функции Оригинальная версия Локализованная версия   RAND СЛЧИС СЛЧИС() – не имеет аргументов RANDBETWEEN СЛУЧМЕЖДУ СЛУЧМЕЖДУ(нижн_граница; верхн_граница)

 

Функция СЛЧИС() возвращает равномерно распределенное случайное число E, большее либо равное 0 и меньшее 1, т.е.: 0 £ E < 1. Вместе с тем, путем несложных преобразований, с ее помощью можно получить любое случайное вещественное число. Например, чтобы получить случайное число между a и b, достаточно задать в любой ячейке ЭТ следующую формулу:

=СЛЧИС()*(b-a)+a

Эта функция не имеет аргументов. Если в ЭТ установлен режим автоматических вычислений, принятый по умолчанию, то возвращаемый функцией результат будет изменяться всякий раз, когда происходит ввод или корректировка данных. В режиме ручных вычислений пересчет всей ЭТ осуществляется только после нажатия клавиши [F9].

Настройка режима управления вычислениями производится установкой соответствующего флажка в подпункте Вычисления пункта Параметры темы Сервис главного меню.

В целом применение данной функции при решении задач финансового анализа ограничено рядом специфических приложений. Однако ее удобно использовать в некоторых случаях для генерации значений вероятности событий, а также вещественных чисел.

Функция СЛУЧМЕЖДУ(нижн_граница; верхн_граница). Как следует из названия этой функции, она позволяет получить случайное число из заданного интервала. При этом тип возвращаемого числа (т.е. вещественное или целое) зависит от типа заданных аргументов.

В качестве примера сгенерируем случайное значение для переменной Q (объем выпуска продукта). Согласно таблице 1, эта переменная принимает значения из диапазона 150 – 300.

Введите в любую ячейку ЭТ формулу:

=СЛУЧМЕЖДУ(150; 300) (Результат: 210).

Если задать аналогичные формулы для переменных P и V, а также формулу для вычисления NPV и скопировать их требуемое число раз, можно получить генеральную совокупность, содержащую различные значения исходных показателей и полученных результатов.

Продемонстрируем изложенный подход на решении примера 1. Перед тем как приступить к разработке шаблона, целесообразно установить в ЭТ режим ручных вычислений. Для этого необходимо выполнить следующие действия.

Выбрать в главном меню тему Сервис.

Выбрать в пункте Параметры подпункт Вычисления.

Установить флажок Вручную и нажать кнопку ОК.

Приступаем к разработке шаблона. С целью упрощения и повышения наглядности анализа выделим для его проведения в рабочей книге ППП EXCEL два листа.

Первый лист – Имитация - предназначен для построения генеральной совокупности (рис. 1). Определенные в данном листе формулы и собственные имена ячеек приведены в таблицах 4 и 5.

Рисунок 1. Лист "Имитация"

Таблица 4 – Формулы листа "Имитация"

Ячейка	Формула
Е7	=B7+10-2
A10	=СЛУЧМЕЖДУ($B$3;$C$3)
A11	=СЛУЧМЕЖДУ($B$3;$C$3)
B10	=СЛУЧМЕЖДУ($B$4;$C$4)
B11	=СЛУЧМЕЖДУ($B$4;$C$4)
C10	=СЛУЧМЕЖДУ($B$5;$C$5)
C11	=СЛУЧМЕЖДУ($B$5;$C$5)
D10	=(B10*(C10-A10)-Пост_расх-Аморт)*(1-Налог)+Аморт
D11	=(B11*(C11-A11)-Пост_расх-Аморт)*(1-Налог)+Аморт
E10	=БС(Норма;Срок;-D10)-Нач_инвест
E11	=БС(Норма;Срок;-D11)-Нач_инвест

 

Таблица 5 – Имена ячеек листа "Имитация"

Адрес ячейки	Имя	Комментарии
Блок A10:A11	Перем_расх	Переменные расходы
Блок B10:B11	Количество	Объем выпуска
Блок C10:C11	Цена	Цена изделия
Блок D10:D11	Поступления	Поступления от проекта NCFt
Блок E10:E11	ЧСС	Чистая современная стоимость NPV

 

Первая часть листа (блок ячеек А1:Е7) предназначена для ввода диапазонов изменений ключевых переменных, значения которых будут генерироваться в процессе проведения эксперимента. В ячейке В7 задается общее число имитаций (экспериментов). Формула, заданная в ячейке Е7, вычисляет номер последней строки выходного блока, в который будут помещены полученные значения. Смысл этой формулы будет раскрыт позже.

Вторая часть листа (блок ячеек А9:Е11) предназначена для проведения имитации. Формулы в ячейках А10:С11 генерируют значения для соответствующих переменных с учетом заданных в ячейках В3:С5 диапазонов их изменений. Обратите внимание на то, что при указании нижней и верхней границы изменений используется абсолютная адресация ячеек.

Формулы в ячейках D10:E11 вычисляют величину потока платежей и его чистую современную стоимость соответственно. При этом значения постоянных переменных берутся из листа шаблона Результаты анализа.

Лист Результаты анализа, кроме значений постоянных переменных, содержит также функции, вычисляющие параметры распределения изменяемых (Q, V, P) и результатных (NCF, NPV) переменных и вероятности различных событий. Определенные для данного листа формулы и собственные имена ячеек приведены в таблицах 6 и 7. Общий вид листа показан на рис. 2.

Таблица 6 – Формулы листа "Результаты анализа"

Ячейка	Формула
B8	=СРЗНАЧ(Перем_расх)
B9	=СТАНДОТКЛОНП(Перем_расх)
B10	=B9/B8
B11	=МИН(Перем_расх)
B12	=МАКС(Перем_расх)
C8	=СРЗНАЧ(Количество)
C9	=СТАНДОТКЛОНП(Количество)
C10	=C9/C8
C11	=МИН(Количество)
C12	=МАКС(Количество)
D8	=СРЗНАЧ(Цена)
D9	=СТАНДОТКЛОНП(Цена)
D10	=D9/D8
D11	=МИН(Цена)
D12	=МАКС(Цена)
E8	=СРЗНАЧ(Поступления)
E9	=СТАНДОТКЛОНП(Поступления)
E10	=E9/E8
E11	=МИН(Поступления)
E12	=МАКС(Поступления)
F8	=СРЗНАЧ(ЧСС)
F9	=СТАНДОТКЛОНП(ЧСС)
F10	=F9/F8
F11	=МИН(ЧСС)
F12	=МАКС(ЧСС)
F13	=СЧЁТЕСЛИ(ЧСС;"<0")
F14	=СУММЕСЛИ(ЧСС;"<0")
F15	=СУММЕСЛИ(ЧСС;">0")
Е18	=НОРМАЛИЗАЦИЯ(D18;$F$8;$F$9)
F18	=НОРМСТРАСП(E18)

 

Таблица 7 – Имена ячеек листа "Результаты анализа"

Адрес ячейки	Имя	Комментарии
B2	Нач_инвест	Начальные инвестиции
B3	Пост_расх	Постоянные расходы
B4	Аморт	Амортизация
D2	Норма	Норма дисконта
D3	Налог	Ставка налога на прибыль
D4	Срок	Срок реализации прока

 

Поскольку формулы листа содержат ряд новых функций, приведем необходимые пояснения.

Функции МИН() и МАКС() вычисляют минимальное и максимальное значение для массива данных из блока ячеек, указанного в качестве их аргумента. Имена и диапазоны этих блоков приведены в таблице 7.

Функция СЧЕТЕСЛИ() осуществляет подсчет количества ячеек в указанном блоке, значения которых удовлетворяют заданному условию. Функция имеет следующий формат:

=СЧЕТЕСЛИ(блок; "условие").

В данном случае заданная в ячейке F13 эта функция осуществляет подсчет количества отрицательных значений NPV, содержащихся в блоке ячеек ЧСС (табл. 7).

Механизм действия функции СУММЕСЛИ() аналогичен функции СЧЕТЕСЛИ(). Отличие заключается лишь в том, что эта функция суммирует значения ячеек в указанном блоке, если они удовлетворяют заданному условию. Функция имеет следующий формат:

=СУММЕСЛИ(блок; "условие")

В данном случае заданные в ячейках F14:F15 функции осуществляют подсчет суммы отрицательных (ячейка F14) и положительных (ячейка F14) значений NPV, содержащихся в блоке ЧСС. Смысл этих расчетов будет объяснен позже.

Две последние формулы (ячейки Е18 и F18) предназначены для проведения вероятностного анализа распределения NPV и требуют небольшого теоретического отступления.

 

Рисунок 2. Лист "Результаты анализа"

 

В рассматриваемом примере мы исходим из предположения о независимости и равномерном распределении ключевых переменных Q, V, P. Однако какое распределение при этом будет иметь результатная величина, показатель NPV, заранее определить нельзя.

Одно из возможных решений этой проблемы – попытаться аппроксимировать неизвестное распределение каким-либо известным. При этом в качестве приближения удобнее всего использовать нормальное распределение. Это связано с тем, что в соответствии с центральной предельной теоремой теории вероятностей при выполнении определенных условий сумма большого числа случайных величин имеет распределение, приблизительно соответствующее нормальному.

В прикладном анализе для целей аппроксимации широко применяется частный случай нормального распределения т.н. стандартное нормальное распределение. Математическое ожидание стандартно распределенной случайной величины Е равно 0: M(E) = 0. График этого распределения симметричен относительно оси ординат, а характеризуется оно всего одним параметром – стандартным отклонением s, равным 1.

Приведение случайной переменной E к стандартно распределенной величине Z осуществляется с помощью т.н. нормализации – вычитания средней и последующего деления на стандартное отклонение:

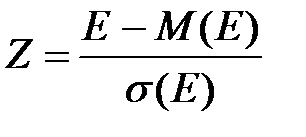,                                                    (2)

Как следует из (2), величина Z выражается в количестве стандартных отклонений. Для вычисления вероятностей по значению нормализованной величины Z используются специальные статистические таблицы.

В ППП EXCEL подобные вычисления осуществляются с помощью статистических функций НОРМАЛИЗАЦИЯ() и НОРМСТРАСП().

Функция НОРМАЛИЗАЦИЯ(x; среднее; станд_откл). Эта функция возвращает нормализованное значение Z величины x, на основании которого затем вычисляется искомая вероятность p(E ≤ x). Она реализует соотношение (2). Функция требует задания трех аргументов:

х – нормализуемое значение;

среднее – математическое ожидание случайной величины Е;

станд_откл – стандартное отклонение.

Полученное значение Z является аргументом для следующей функции – НОРМСТРАСП().

Функция НОРМСТРАСП(Z). Эта функция возвращает стандартное нормальное распределение, т.е. вероятность того, что случайная нормализованная величина Е будет меньше или равна х. Она имеет всего один аргумент – Z, вычисляемый функцией НОРМАЛИЗАЦИЯ().

Нетрудно заметить, что эти функции следует использовать в тандеме. При этом наиболее эффективным и компактным способом их задания является указание функции НОРМАЛИЗАЦИЯ() в качестве аргумента функции – НОРМСТРАСП(), т.е.:

=НОРМСТРАСП(НОРМАЛИЗАЦИЯ(x; среднее; станд_откл)).

С целью повышения наглядности в проектируемом шаблоне функции заданы раздельно (ячейки Е18 и F18).

Сформируйте данный шаблон и сохраните его на магнитном диске под именем SIMUL_1.XLT. Приступаем к имитационному эксперименту. Для его проведения необходимо выполнить следующие шаги.

1. Ввести значения постоянных переменных (табл. 2) в ячейки В2:В4 и D2:D4 листа Результаты анализа.

2. Ввести значения диапазонов изменений ключевых переменных (табл. 1) в ячейки В3:С5 листа Имитация.

3. Задать в ячейке В7 требуемое число экспериментов.

4. Установить курсор в ячейку А11 и вставить необходимое число строк в шаблон (номер последней строки будет вычислен в Е7).

5. Скопировать формулы блока А10:Е10 требуемое количество раз.

6. Перейти к листу Результаты анализа и проанализировать полученные результаты.

Рассмотрим реализацию выделенных шагов более подробно. Выполнение первых трех пунктов не должно вызвать особых затруднений. Введите значения постоянных переменных в ячейки В2:В4 листа Результаты анализа. Введите значения диапазонов изменений ключевых переменных в ячейки В3:С5 листа Имитация. Укажите в ячейке В7 число проводимых экспериментов, например 500. Установите табличный курсор в ячейку А11.

На следующем шаге необходимо вставить в шаблон нужное количество строк (498) . Однако выделение такого количества строк при помощи указателя мыши – достаточно трудоемкая операция. К счастью ППП EXCEL предоставляет более эффективные процедуры для выполнения подобных операций. В частности, в данном случае можно воспользоваться операцией перехода, которую удобно применять и для выделения больших диапазонов ячеек.

Нажмите функциональную клавишу [F5]. На экране появится окно диалога Переход (рис. 3).

Рисунок 3. Окно диалога "Переход"

 

Для перехода к нужному участку электронной таблицы достаточно указать в поле Ссылка адрес или имя соответствующей ячейки (блока). В данном случае таким адресом будет любая ячейка последней вставляемой строки, номер которой вычислен в ячейке Е7 (508). Например, в качестве адреса перехода может быть указана ячейка А508.

Введите в поле Ссылка адрес: А508 и нажмите комбинацию клавиш [SHIFT] + [ENTER]. Результатом выполнения этих действий будет выделение блока А11: А508. После этого осуществите вставку строк любым из известных вам способов.

Теперь необходимо заполнить вставленные строки формулами блока ячеек А10:Е10. Для этого выполните следующие действия.

1. Выделите и скопируйте в буфер блок ячеек А10:Е10.

2. Нажмите комбинацию клавиш [CTRL] + [SHIFT] + [¯ ].

3. Нажмите клавишу [ENTER].

4. Нажмите клавишу [F9] .

Результатом выполнения этих действий будет заполнение блока А10:Е509 случайными значениями ключевых переменных V, Q, P и результатами вычислений величин NCF и NPV. Фрагмент результатов имитации, полученных автором, приведен на рис. 4. Соответствующие проведенному эксперименту результаты анализа приведены на рис. 5.

Рисунок 4. Результаты имитации

Сумма всех отрицательных значений NPV в полученной генеральной совокупности (ячейка F14) может быть интерпретирована как чистая стоимость неопределенности для инвестора в случае принятия проекта. Аналогично сумма всех положительных значений NPV (ячейка F15) может трактоваться как чистая стоимость неопределенности для инвестора в случае отклонения проекта. Несмотря на всю условность этих показателей, в целом они представляют собой индикаторы целесообразности проведения дальнейшего анализа.

Вывод: В данном случае они наглядно демонстрируют несоизмеримость суммы возможных убытков по отношению к общей сумме доходов (-11691,92 и 1692669,76 соответственно).

Повышенный уровень

Упражнение 2.

На практике одним из важнейших этапов анализа результатов имитационного эксперимента является исследование зависимостей между ключевыми параметрами. Известно, что количественная оценка вариации напрямую зависит от степени корреляции между случайными величинами. Методы оценки степени зависимости, а также технология ее автоматизации путем применения специальных инструментов ППП EXCEL будут продемонстрированы ниже. Здесь же мы ограничимся визуальным (графическим) исследованием. На рис. 6 приведен график распределения значений ключевых параметров V, P и Q, построенный на основании 75 имитаций.

Рисунок 5. Результаты анализа

Нетрудно заметить, что в целом вариация значений всех трех параметров носит случайный характер, что подтверждает принятую ранее гипотезу о их независимости. Для сравнения ниже приведен график распределений потока платежей NCF и величины NPV (рис. 7).

Как и следовало ожидать, направления колебаний здесь в точности совпадают и между этими величинами существует сильная корреляционная связь, близкая к функциональной. Дальнейшие расчеты показали, что величина коэффициента корреляции между полученными распределениями NCF и NPV оказалась равной 1.

Подводя итоги, отметим, что в целом применение рассмотренной технологии проведения имитационных экспериментов в среде EXCEL – достаточно трудоемкий процесс, который к тому же ограничивается случаем равномерного распределения исследуемых переменных.

Гораздо более удобным и эффективным способом решения таких задач в среде ППП EXCEL является использование специального инструмента анализа – Генератор случайных чисел.

Рисунок 6. Распределение значений параметров V, P и Q

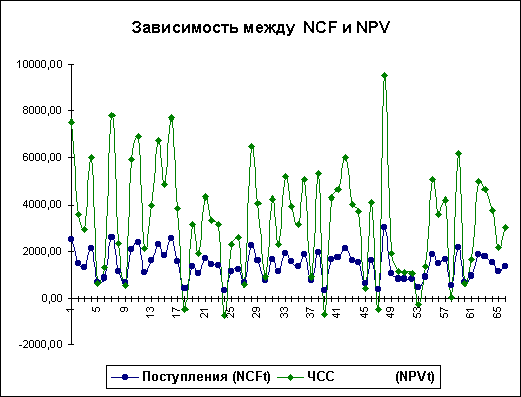
Рисунок 7. Зависимость между NCF и NPV

Содержание отчета и его форма

Отчет к лабораторной работе оформляется в виде текстового документа по форме простого реферата и должен включать:

1. Название лабораторной работы.

2. Цель и содержание лабораторной работы.

3. Краткие выводы по результатам выполнения заданий к лабораторной работе.

4. Формулировку задания для самостоятельной работы и результат его выполнения.

Задания для самостоятельной работы

Базовый уровень

1. Способы имитационного эксперимента для моделирования инвестиционных рисков.

2. Объяснить технологию имитационного решения задачи в данной работе.

3. Перечислить исходные данные для параметров, переменных и показателей модели.

Повышенный уровень

4. Какие математические функции используются для имитационного эксперимента в данной работе.

5. Согласно варианту рассчитать имитационную модель инвестиционных рисков.

Варианты

1. Ключевые параметры проекта по производству продукта "А"

Сценарий

Показатели

Наихудший Наилучший Вероятный Объем выпуска – Q 125 275 175 Цена за штуку – P 37 52 47 Переменные затраты – V 30 20 25

Неизменяемые параметры проекта по производству продукта "А"

Показатели	Наиболее вероятное значение
Постоянные затраты – F	300
Амортизация – A	50
Налог на прибыль – T	50%
Норма дисконта – r	10%
Срок проекта – n	5
Начальные инвестиции – I0	1000

Нормальное распределение ключевых переменных

Количество имитаций – 300.

2. Ключевые параметры проекта по производству продукта "А"

Сценарий	Показатели
	Наихудший	Наилучший	Вероятный
Объем выпуска – Q	121	271	171
Цена за штуку – P	30	45	40
Переменные затраты – V	31	21	26

 

Неизменяемые параметры проекта по производству продукта "А"

Показатели	Наиболее вероятное значение
Постоянные затраты – F	600
Амортизация – A	100
Налог на прибыль – T	65%
Норма дисконта – r	15%
Срок проекта – n	5
Начальные инвестиции – I0	3000

Нормальное распределение ключевых переменных

Количество имитаций – 400.

3. Ключевые параметры проекта по производству продукта "А"

Сценарий	Показатели
	Наихудший	Наилучший	Вероятный
Объем выпуска – Q	136	286	186
Цена за штуку – P	35	50	45
Переменные затраты – V	33	23	28

Неизменяемые параметры проекта по производству продукта "А"

Показатели	Наиболее вероятное значение
Постоянные затраты – F	450
Амортизация – A	100
Налог на прибыль – T	70%
Норма дисконта – r	20%
Срок проекта – n	5
Начальные инвестиции – I0	1500

Нормальное распределение ключевых переменных

Количество имитаций – 350.

4. Ключевые параметры проекта по производству продукта "А"

Сценарий	Показатели
	Наихудший	Наилучший	Вероятный
Объем выпуска – Q	132	282	182
Цена за штуку – P	28	43	38
Переменные затраты – V	29	19	24

Неизменяемые параметры проекта по производству продукта "А"

Показатели	Наиболее вероятное значение
Постоянные затраты – F	350
Амортизация – A	100
Налог на прибыль – T	55%
Норма дисконта – r	8%
Срок проекта – n	4
Начальные инвестиции – I0	1000

Нормальное распределение ключевых переменных

Количество имитаций – 450.

5. Ключевые параметры проекта по производству продукта "А"

Сценарий	Показатели
	Наихудший	Наилучший	Вероятный
Объем выпуска – Q	130	280	180
Цена за штуку – P	25	40	35
Переменные затраты – V	25	15	20

Неизменяемые параметры проекта по производству продукта "А"

Показатели	Наиболее вероятное значение
Постоянные затраты – F	400
Амортизация – A	80
Налог на прибыль – T	60%
Норма дисконта – r	12%
Срок проекта – n	5
Начальные инвестиции – I0	1200

Нормальное распределение ключевых переменных

Количество имитаций – 550.

6. Ключевые параметры проекта по производству продукта "А"

Сценарий	Показатели
	Наихудший	Наилучший	Вероятный
Объем выпуска – Q	136	286	186
Цена за штуку – P	24	39	34
Переменные затраты – V	26	16	21

Неизменяемые параметры проекта по производству продукта "А"

Показатели	Наиболее вероятное значение
Постоянные затраты – F	550
Амортизация – A	150
Налог на прибыль – T	55%
Норма дисконта – r	12%
Срок проекта – n	5
Начальные инвестиции – I0	1800

Нормальное распределение ключевых переменных

Количество имитаций – 380.

7. Ключевые параметры проекта по производству продукта "А"

Сценарий	Показатели
	Наихудший	Наилучший	Вероятный
Объем выпуска – Q	142	292	192
Цена за штуку – P	23	38	33
Переменные затраты – V	24	14	19

Неизменяемые параметры проекта по производству продукта "А"

Показатели	Наиболее вероятное значение
Постоянные затраты – F	480
Амортизация – A	90
Налог на прибыль – T	57%
Норма дисконта – r	9%
Срок проекта – n	4,5
Начальные инвестиции – I0	1700

Нормальное распределение ключевых переменных

Количество имитаций – 490.

8. Ключевые параметры проекта по производству продукта "А"

Сценарий	Показатели
	Наихудший	Наилучший	Вероятный
Объем выпуска – Q	145	295	195
Цена за штуку – P	31	46	41
Переменные затраты – V	25	15	20

Неизменяемые параметры проекта по производству продукта "А"

Показатели	Наиболее вероятное значение
Постоянные затраты – F	560
Амортизация – A	95
Налог на прибыль – T	61%
Норма дисконта – r	11%
Срок проекта – n	5,5
Начальные инвестиции – I0	2200

Нормальное распределение ключевых переменных

Количество имитаций – 475.

9. Ключевые параметры проекта по производству продукта "А"

Сценарий	Показатели
	Наихудший	Наилучший	Вероятный
Объем выпуска – Q	155	305	205
Цена за штуку – P	42	57	52
Переменные затраты – V	43	33	38

Неизменяемые параметры проекта по производству продукта "А"

Показатели	Наиболее вероятное значение
Постоянные затраты – F	530
Амортизация – A	120
Налог на прибыль – T	65%
Норма дисконта – r	14%
Срок проекта – n	5
Начальные инвестиции – I0	3000

Нормальное распределение ключевых переменных

Количество имитаций – 550.

10. Ключевые параметры проекта по производству продукта "А"

Сценарий	Показатели
	Наихудший	Наилучший	Вероятный
Объем выпуска – Q	160	310	210
Цена за штуку – P	54	69	64
Переменные затраты – V	47	37	42

Неизменяемые параметры проекта по производству продукта "А"

Показатели	Наиболее вероятное значение
Постоянные затраты – F	530
Амортизация – A	130
Налог на прибыль – T	61%
Норма дисконта – r	11%
Срок проекта – n	5
Начальные инвестиции – I0	2600

 

Нормальное распределение ключевых переменных

Количество имитаций – 510.

 

 

Лабораторная работа 3-4

Теоретическая часть

Инструмент Генератор случайных чисел предназначен для автоматической генерации множества данных (генеральной совокупности) заданного объема, элементы которого характеризуются определенным распределением вероятностей. При этом могут быть использованы 7 типов распределений: равномерное, нормальное, Бернулли, Пуассона, биномиальное, модельное и дискретное. Применение инструмента Генератор случайных чисел, как и большинства используемых в этой работе функций, требует установки специального дополнения Пакет анализа.

Задания к лабораторному занятию

Базовый уровень

Упражнение 1.

Для демонстрации техники применения инструмента Генератор случайных чисел изменим условия примера 1, определив вероятности для каждого сценария развития, как показано в таблице 1. Мы также будем исходить из предположения о нормальном распределении ключевых переменных. Количество имитаций оставим прежним – 500.

Таблица 1 – Вероятностные сценарии реализации проекта

Сценарий Показатели	Наихудший P = 0.25	Наилучший P = 0.25	Вероятный P = 0.5
Объем выпуска – Q	150	300	200
Цена за штуку – P	40	55	50
Переменные затраты – V	35	25	30

 

Приступим к формированию шаблона. Как и в предыдущем случае, выделим в рабочей книге два листа: Имитация и Результаты анализа.

Формирование шаблона целесообразно начать с листа Результаты анализа (рис. 1).

Рисунок 1. Лист "Результаты анализа" (шаблон II)

 

Таблица 2 – Формулы листа "Результаты анализа" (шаблон II)

Ячейка	Формула
В17	=НОРМРАСП(0;B8;B9;1)
В18	=НОРМРАСП(B11;B8;B9;1)
В19	=НОРМРАСП(B12;B8;B9;1)-НОРМРАСП(B8+B9;B8;B9;1)
В20	=НОРМРАСП(B8;B8;B9;1)-НОРМРАСП(B8-B9;B8;B9;1)
С17	=НОРМРАСП(0;C8;C9;1)
С18	=НОРМРАСП(C11;C8;C9;1)
С19	=НОРМРАСП(C12;C8;C9;1)-НОРМРАСП(C8+C9;C8;C9;1)
С20	=НОРМРАСП(C8;C8;C9;1)-НОРМРАСП(C8-C9;C8;C9;1)
D17	=НОРМРАСП(0;D8;D9;1)
D18	=НОРМРАСП(D11;D8;D9;1)
D19	=НОРМРАСП(D12;D8;D9;1)-НОРМРАСП(D8+D9;D8;D9;1)
D20	=НОРМРАСП(D8;D8;D9;1)-НОРМРАСП(D8-D9;D8;D9;1)
E17	=НОРМРАСП(0;E8;E9;1)
E18	=НОРМРАСП(E11;E8;E9;1)
E19	=НОРМРАСП(E12;E8;E9;1)-НОРМРАСП(E8+E9;E8;E9;1)
E20	=НОРМРАСП(E8;E8;E9;1)-НОРМРАСП(E8-E9;E8;E9;1)
F17	=НОРМРАСП(0;F8;F9;1)
F18	=НОРМРАСП(F11;F8;F9;1)
F19	=НОРМРАСП(F12;F8;F9;1)-НОРМРАСП(F8+F9;F8;F9;1)
F20	=НОРМРАСП(F8;F8;F9;1)-НОРМРАСП(F8-F9;F8;F9;1)

 

Используемые в нем собственные имена ячеек также взяты из аналогичного листа предыдущего шаблона (см. табл. 7 из лабораторной работы №1-2).

Для быстрого формирования нового листа Результаты анализа выполните следующие действия.

1. Загрузите предыдущий шаблон SIMUL_1.XLT и сохраните его под другим именем, например – SIMUL_2.XLT

2. Удалите лист Имитация. Для этого установите указатель мыши на ярлычок этого листа и нажмите правую кнопку. Результатом выполнения этих действий будет появление списка операций в виде контекстного меню. Выберите операцию Удалить. Подтвердите свое решение нажатием кнопки ОК в появившемся диалоговом окне.

3. Перейдите в лист Результаты анализа. Удалите строки 17–18. Откорректируйте заголовок ЭТ.

4. Добавьте формулы из таблицы 2. Для этого введите соответствующие формулы в ячейки блока В17:В20 и скопируйте их в блок С17:F20. Введите соответствующие комментарии.

5. Сверьте полученную таблицу с рис. 1.

Перейдите к следующему листу и присвойте ему имя Имитация. Приступаем к его формированию (рис. 2).

Рисунок 2. Лист "Имитация" (шаблон II)

Первая часть этого листа (блок ячеек А1:Е10) предназначена для ввода исходных данных и расчета необходимых параметров их распределений. Напомним, что нормальное распределение случайной величины характеризуется двумя параметрами – математическим ожиданием (средним) и стандартным отклонением. Формулы расчета указанных параметров для ключевых переменных модели заданы в блоках ячеек В7:D7 и B8:D8 соответственно (табл. 4). Для удобства определения формул и повышения их наглядности блоку ячеек Е3:Е5 присвоено имя Вероятности (табл. 3).

Таблица 3 – Имена ячеек листа "Имитация" (шаблон II)

Адрес ячейки	Имя	Комментарии
Блок Е3:Е5	Вероятности	Вероятность значения параметра
Блок A13:A512	Перем_расх	Переменные расходы
Блок B13:B512	Количество	Объем выпуска
Блок C13:C512	Цена	Цена изделия
Блок D13:D512	Поступления	Поступления от проекта NCF
Блок E13:E512	ЧСС	Чистая современная стоимость NPV

Таблица 4 – Формулы листа "Имитация" (шаблон II)

Ячейка	Формула
В7	=СУММПРОИЗВ(B3:B5; Вероятности)
В8	{=КОРЕНЬ(СУММПРОИЗВ((B3:B5 - B7)^2; Вероятности))}
С7	=СУММПРОИЗВ(C3:C5; Вероятности)
С8	{=КОРЕНЬ(СУММПРОИЗВ((C3:C5 - C7)^2; Вероятности))}
D7	=СУММПРОИЗВ(D3:D5; Вероятности)
D8	{=КОРЕНЬ(СУММПРОИЗВ((D3:D5 - D7)^2; Вероятности))}
E10	=B10+13 –1
D13	=(B13*(C13-A13)-Пост_расх-Аморт)*(1-Налог)+Аморт
E13	=ПЗ(Норма; Срок; -D13) - Нач_инвест

 

Обратите внимание на то, что для расчета стандартных отклонений используются формулы-массивы.. Для формирования блока формул достаточно определить их для ячеек В7:В8 и затем скопировать в блок С7:D8.

Формула в ячейке Е10 по заданному числу имитаций (ячейка В10) вычисляет номер последней строки для блоков, в которых будут храниться сгенерированные значения ключевых переменных.

Ячейки D13:E13 содержат уже знакомые нам формулы для расчета величины потока платежей NCF и его чистой современной стоимости NPV.

Сформируйте элементы оформления листа Имитация, определите необходимые имена для блоков ячеек (табл. 3) и задайте требуемые формулы (табл. 4). Сохраните полученный шаблон под именем SIMUL_2.XLT.

Введите исходные значения постоянных переменных (табл. 2 лабораторной работы №1-2) в ячейки В2:В4 и D2:D4 листа Результаты анализа. Перейдите к листу Имитация. Введите значения ключевых переменных и соответствующие вероятности (табл. 1). Полученная в результате ЭТ должна иметь вид рисунка 3.

Рисунок 3. Лист "Имитация" после ввода исходных данных

 

Установите курсор в ячейку А13. Приступаем к проведению имитационного эксперимента.

1. Выберите в главном меню тему Сервис, пункт Анализ данных. Результатом выполнения этих действий будет появление диалогового окна Анализ данных, содержащего список инструментов анализа.

2. Выберите из списка Инструменты анализа пункт Генерация случайных чисел и нажмите кнопку ОК (рис. 4).

3. На экране появится диалоговое окно Генерация случайных чисел. Укажите в списке Распределения требуемый тип – Нормальное. Заполните остальные поля изменившегося окна согласно рисунку 5 и нажмите кнопку ОК. Результатом будет заполнение блока ячеек А13: А512 (переменные расходы) сгенерированными случайными значениями.

Рисунок 4. Выбор инструмента "Генерация случайных чисел"

 

Приведем необходимые пояснения. Первым заполняемым аргументом диалогового окна Генерация случайных чисел является поле Число переменных. Оно задает количество колонок ЭТ, в которых будут размещаться сгенерированные в соответствии с заданным законом распределения случайные величины. В нашем примере оно должно содержать 1, так как ранее мы отвели под значения переменной V (переменные расходы) в ЭТ одну колонку – А. Если указывается число больше 1, случайные величины будут размещены в соответствующем количестве соседних колонок, начиная с активной ячейки. Если это число не введено, то все колонки в выходном диапазоне будут заполнены.

Следующим обязательным аргументом для заполнения является содержимое поля Число случайных чисел (т.е. – количество имитаций). Согласно условиям примера оно должно быть равно 500 (рис. 5). При этом ППП EXCEL автоматически подсчитывает необходимое количество ячеек для хранения генеральной совокупности.

 

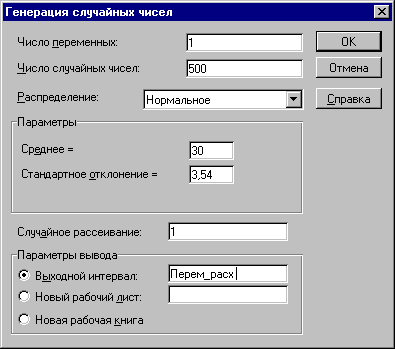
Рисунок 5. Заполнение полей окна "Генерация случайных чисел"

 

Необходимый вид распределения задается путем соответствующего выбора из списка Распределения. Как уже отмечалось ранее, могут быть получены 7 наиболее распространенных в практическом анализе типов распределений, каждое из которых характеризуется собственными параметрами. Выбранный тип распределения определяет внешний вид диалогового окна. В рассматриваемом примере выбор типа распределения Нормальное повлек за собой появление дополнительных аргументов – его параметров Среднее и Стандартное отклонение, рассчитанных ранее для исследуемой переменной V в ячейках В7 и В8 листа Имитация. К сожалению, эти аргументы могут быть заданы только в виде констант. Использование адресов ячеек и собственных имен здесь не допускается!

Указание аргумента Случайное рассеивание позволяет при повторных запусках генератора получать те же значения случайных величин, что и при первом. Таким образом, одну и ту же генеральную совокупность случайных чисел можно получить несколько раз, что значительно повышает эффективность анализа (сравните с предыдущим шаблоном!). Если этот аргумент не задан (равен 0), при каждом последующем запуске генератора будет формироваться новая генеральная совокупность. В нашем примере этот аргумент задан равным 1, что позволит нам оперировать с одной и той же генеральной совокупностью и избежать постоянных перерасчетов ЭТ.

Последний аргумент диалогового окна Генерация случайных чисел – Параметры вывода определяет место расположения полученных результатов. Место вывода задается путем установления соответствующего флажка. При этом можно выбрать три варианта размещения:

· выходной блок ячеек на текущем листе. Введите ссылку на левую верхнюю ячейку выходного диапазона, при этом его размер будет определен автоматически, и в случае возможного наложения генерируемых значений на уже имеющиеся данные на экран будет выведено предупреждающее сообщение;

· новый рабочий лист. В рабочей книге будет открыт новый лист, содержащий результаты генерации случайных величин, начиная с ячейки A1;

· новая рабочая книга. Будет открыта новая книга с результатами имитации на первом листе.

Повышенный уровень

Упражнение 2.

В рассматриваемом примере для проведения дальнейшего анализа необходимо, чтобы случайные величины размещались в специально отведенных для них блоках ячеек (табл. 3). В частности, для хранения 500 значений первой переменной ранее был отведен блок ячеек А13: А512. Поскольку для этого блока определено собственное имя Перем_расх, оно указано в качестве выходного диапазона. Отметим, что при увеличении либо уменьшении количества имитаций необходимо также переопределить и выходные блоки, предназначенные для хранения значений переменных.

Генерация значений остальных переменных Q и Р осуществляется также путем выполнения шагов 1–3. Пример заполнения окна Генерация случайных чисел для переменной Q (количество) приведен на рис. 6.

Для получения генеральной совокупности значений потока платежей и их чистой современной стоимости необходимо скопировать формулы базовой строки (ячейки D13:E13) требуемое число раз (499). С проблемой копирования больших диапазонов ячеек мы уже сталкивались в предыдущем примере.

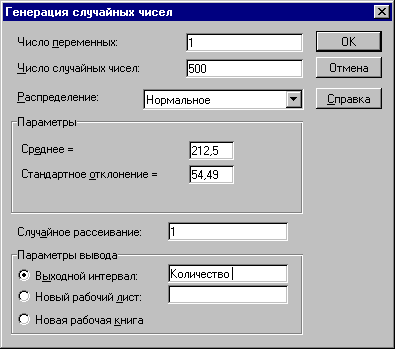
Рисунок 6. Заполнение полей окна для переменной Q

 

Ее решение осуществляется выполнением следующих действий.

1. Выделите и скопируйте в буфер ячейку D13.

2. Нажмите клавишу [F5]. На экране появится диалоговое окно Переход.

3. Укажите в поле Ссылка имя блока Поступления и нажмите кнопку ОК. Результатом этих действий будет выделение заданного блока.

4. Нажмите клавишу [ENTER].

5. Если в ЭТ был установлен режим ручных вычислений, нажмите клавишу [F9].

6. Аналогичным образом копируется формула из ячейки Е13. При этом в поле Ссылка диалогового окна Переход необходимо указать имя блока ЧСС. Вы также можете выбрать необходимое имя из списка Перейти к.

Полученные результаты решения примера приведены на рис. 7 – 8.

Вывод: Результаты проведенного имитационного эксперимента ненамного отличаются от предыдущих. Величина ожидаемой NPV равна 3412,14 при стандартном отклонении 2556,83. Коэффициент вариации (0,75) несколько выше, но меньше 1, таким образом, риск данного проекта в целом ниже среднего риска инвестиционного портфеля фирмы. Результаты вероятностного анализа показывают, что шанс получить отрицательную величину NPV не превышает 9%. Общее число отрицательных значений NPV в выборке составляет 32 из 500. Таким образом, с вероятностью около 91% можно утверждать, что чистая современная стоимость проекта будет больше 0. При этом вероятность того, что величина NPV окажется больше чем М(NPV) + s , равна 16% (ячейка F19). Вероятность попадания значения NPV в интервал [М(NPV) - s ; М(NPV)] равна 34%.

Рисунок 7. Результаты имитационного эксперимента (шаблон II)

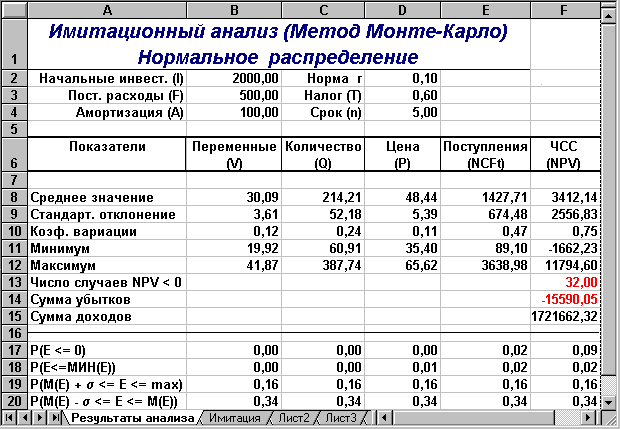
Рисунок 8. Результаты анализа (шаблон II)

Содержание отчета и его форма

Отчет к лабораторной работе оформляется в виде текстового документа по форме простого реферата и должен включать:

1. Название лабораторной работы.

2. Цель и содержание лабораторной работы.

3. Краткие выводы по результатам выполнения заданий к лабораторной работе.

4. Формулировку задания для самостоятельной работы и результат его выполнения.

Задания для самостоятельной работы

Базовый уровень

1. Объяснить технологию проведения имитационных экспериментов для использования инструмента "Генератора случайных чисел".

2. Перечислить исходные данные для параметров, переменных и показателей модели.

3. Какие математические функции используются для имитационного эксперимента в данной работе.

Повышенный уровень

4. Согласно варианту задания из лабораторной работы 1-2 выполнить имитационные эксперименты с использованием инструмента «Генератора случайных чисел».

 

Лабораторная работа 5

Теоретическая часть

В анализе стохастических процессов важное значение имеют статистические взаимосвязи между случайными величинами. В качестве количественных характеристик подобных взаимосвязей в статистике используют два показателя: ковариацию и корреляцию.

Ковариация выражает степень статистической зависимости между двумя множествами данных и определяется из следующего соотношения:

,                                        (1)

где X, Y – множество значений случайных величин размерности m; M(X) – математическое ожидание случайной величины Х; M(Y) – математическое ожидание случайной величины Y.

Как следует из (1), положительная ковариация наблюдается в том случае, когда большим значениям случайной величины Х соответствуют большие значения случайной величины Y, т.е. между ними существует тесная прямая взаимосвязь. Соответственно отрицательная ковариация будет иметь место при соответствии малым значениям случайной величины Х больших значений случайной величины Y. При слабовыраженной зависимости значение показателя ковариации близко к 0.

Ковариация зависит от единиц измерения исследуемых величин, что ограничивает ее применение на практике. Более удобным для использования в анализе является производный от нее показатель – коэффициент корреляции R, вычисляемый по формуле:

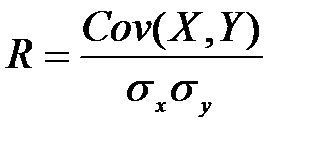,                                                                                                (2)

Коэффициент корреляции обладает теми же свойствами, что и ковариация, однако является безразмерной величиной и принимает значения от -1 (характеризует линейную обратную взаимосвязь) до +1 (характеризует линейную прямую взаимосвязь). Для независимых случайных величин значение коэффициента корреляции близко к 0.

Определение количественных характеристик для оценки тесноты взаимосвязи между случайными величинами в ППП EXCEL может быть осуществлено двумя способами:

– с помощью статистических функций КОВАР() и КОРРЕЛ();

– с помощью специальных инструментов статистического анализа.

Если число исследуемых переменных больше 2, более удобным является использование инструментов анализа.

Задания к лабораторному занятию

Базовый уровень

Упражнение 1. Инструмент анализа данных "Корреляция"

Определим степень тесноты взаимосвязей между переменными V, Q, P, NCF и NPV. При этом в качестве меры будем использовать показатель корреляции R.

1. Выберите в главном меню тему Сервис, пункт Анализ данных. Результатом выполнения этих действий будет появление диалогового окна Анализ данных, содержащего список инструментов анализа.

2. Выберите из списка Инструменты анализа пункт Корреляция и нажмите кнопку ОК (рис. 1). Результатом будет появление окна диалога инструмента Корреляция.

3. Заполните поля диалогового окна, как показано на рис. 2 и нажмите кнопку ОК.

4. Вид полученной ЭТ после выполнения элементарных операций форматирования приведен на рис. 3.

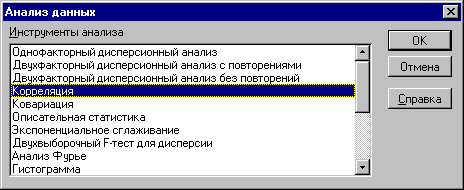
Рисунок 1. Список инструментов анализа (выбор пункта "Корреляция")

 

Рисунок 2. Заполнение окна диалога инструмента "Корреляция"

 

Рисунок 3. Результаты корреляционного анализа

Результаты корреляционного анализа представлены в ЭТ в виде квадратной матрицы, заполненной только наполовину, поскольку значение коэффициента корреляции между двумя случайными величинами не зависит от порядка их обработки. Нетрудно заметить, что эта матрица симметрична относительно главной диагонали, элементы которой равны 1, так как каждая переменная коррелирует сама с собой.

Вывод: Как следует из результатов корреляционного анализа, выдвинутая в процессе решения предыдущего примера гипотеза о независимости распределений ключевых переменных V, Q, P в целом подтвердилась. Значения коэффициентов корреляции между переменными расходами V, количеством Q и ценой Р (ячейки В3:В4, С4) достаточно близки к 0.

В свою очередь, величина показателя NPV напрямую зависит от величины потока платежей (R = 1). Кроме того, существует корреляционная зависимость средней степени между Q и NPV (R = 0,548), P и NPV (R = 0,67). Как и следовало ожидать, между величинами V и NPV существует умеренная обратная корреляционная зависимость (R = -0,39).

Полезность проведения последующего статистического анализа результатов имитационного эксперимента заключается также в том, что во многих случаях он позволяет выявить некорректности в исходных данных, либо даже ошибки в постановке задачи. В частности, отсутствие в рассматриваемом примере, взаимосвязи между переменными затратами V и объемами выпуска продукта Q требует дополнительных объяснений, так как с увеличением последнего, величина V также должна расти. Таким образом, установленный диапазон изменений переменных затрат V нуждается в дополнительной проверке и, возможно, корректировке.

Следует отметить, что близкие к нулевым значения коэффициента корреляции R указывают на отсутствие линейной связи между исследуемыми переменными, но не исключают возможности нелинейной зависимости. Кроме того, высокая корреляция необязательно всегда означает наличие причинной связи, так как две исследуемые переменные могут зависеть от значений третьей.

При проведении имитационного эксперимента и последующего вероятностного анализа полученных результатов мы исходили из предположения о нормальном распределении исходных и выходных показателей. Вместе с тем справедливость сделанных допущений, по крайней мере для выходного показателя NPV, нуждается в проверке.

Для проверки гипотезы о нормальном распределении случайной величины применяются специальные статистические критерии: Колмогорова-Смирнова, w ², c ². В целом ППП EXCEL позволяет быстро и эффективно осуществить расчет требуемого критерия и провести статистическую оценку гипотез.

Однако в простейшем случае для этих целей можно использовать такие характеристики распределения, как асимметрия (скос) и эксцесс. Следует напомнить, что для нормального распределения эти характеристики должны быть равны 0. На практике близкими к нулевым значениями можно пренебречь. Для вычисления коэффициента асимметрии и эксцесса в ППП EXCEL реализованы специальные статистические функции – СКОС() и ЭКСЦЕСС().

Полезным инструментом анализа данных ППП EXCEL является Описательная статистика.

Повышенный уровень

Содержание отчета и его форма

Отчет к лабораторной работе оформляется в виде текстового документа по форме простого реферата и должен включать:

1. Название лабораторной работы.

2. Цель и содержание лабораторной работы.

3. Краткие выводы по результатам выполнения заданий к лабораторной работе.

4. Формулировку задания для самостоятельной работы и результат его выполнения.

Задания для самостоятельной работы

Базовый уровень

1. Показатели статистического анализа результатов.

2. Технология проведения статистического анализа средствами MS Excel.

Повышенный уровень

3. Согласно варианту из лабораторной работы 1-2 рассчитать показатели статистического анализа.

Лабораторная работа 6-7

Теоретическая часть

1. Эволюция системы моделирования Vensim. Язык моделирования Vensim создан фирмой Ventana Systems, основанной в 1985 г. в Гарварде (штат Массачусетс). Этот язык моделирования базируется на языке программирования Pascal. На­чиная с 1998 г. язык Vensim и поддерживающие системы были привязаны к языку С и графической оболочке X-Windows. В 1991 г. была разработана версия Vensim-1.50 для экспертных ди­намических моделей (имитационных моделей).

В 1993 г. появилась новая версия Vensim-1.60, которая была наиболее адаптирована для пользователя. Эта версия имела не­сколько модификаций для профессиональных и непрофессиональ­ных пользователей - Standard, Professional и DSS . В 1994 фирмой была создана версия Vensim - 1.61, а в 1994 г. - версия Vensim - 1.62, которая была связана с операционной системой Macintoch, способной проводить вероятностное моделирование. Эта версия имеет модельный ридер, аналогичный Adob Acrobat. В 1996 г кон­фигурации Vensim названы Vensim Personal Learning Edition (Ven­sim PLE). Vensim PLE наиболее приемлем для обучения и работы индивидуальных пользователей, конструирующих несложные мо­дели. Версия Vensim PLE является некоммерческой. Фирма Ventana Systems постоянно модифицирует свои программные продук­ты. Так, в 1997 г. создана версия Vensim 3.0, включающая Vensim Model Reader и Vensim DLL, которая может быть использована такими языками программирования и средами разработки как С, C++, Visual Basic, Delphi и др.

В 1999 г. выпущена версия Vensim 4, имеющая удобный пользовательский интерфейс, содержащий новые объекты, такие как контроль входа-выхода для мини-применений и др. Новая конфигурация получила название Vensim PLE Plus. В 2002 г. раз­работана версия Vensim 5.0, являющаяся первой версией, имею­щей SyntheSim, который позволяет выполнять моделирование дос­таточно быстро и сразу видеть его результаты. В 2003 г. фирмой выпущена версия Vensim 5.1 с поддержкой ODBC. Интерфейс вы­пущенной в этом же году версии Vensim 5.2 позволяет более удоб­но пользоваться справочной системой Vensim. Разработанная в 2004 г. версия Vensim 5.3 дает возможность ссылок на Web-страницы и другие файлы вне модели. Разработка в 2004 г. версии Vensim 5.4 расширила обучающие возможности Vensim PLE, ко­торый имеет удобный пользовательский интерфейс, основанный на визуальном моделировании.

Возможности Vensim PLE, PLE Plus, Standard, Professional и DSS различны, и это отражается на интерфейсе этих версий (пане­ли инструментов), хотя в панель инструментов любой версии мо­гут быть внесены изменения.

Средства анализа

Инструментальные средства анализа используются для ото­бражения информации о рабочих переменных, их места и значения в модели.

Causes tree (Дерево причин) создает древовидное графи­ческое представление, показывающее взаимосвязь рабочих переменных. Uses tree (Дерево следствий) создает древовидное графи­ческое представление, показывающее использование рабочих переменных. Loops (Циклы) отображает список всех циклов с обратной связью, проходящих через рабочие переменные. Document (Документ) позволяет провести обзор выраже­ний, определений и измеряющих устройств для всей модели. Causes strip graph (Причинно-следственный граф) ото­бражает простые графы на полосе, позволяет проследить влияние взаимосвязанных переменных друг на друга. Graph (Граф) отображает поведение рабочей переменной на графике. Table (Таблица) генерирует таблицу для выбранной рабо­чей переменной. Runs compare (Сравнение прогонов) сравнивает все перемен­ные и константы в первом прогоне модели с переменными и кон­стантами, загруженными во втором прогоне модели.

 

Строка состояния

Строка состояния показывает состояние схемы модели и на­ходящихся на ней объектов. Она содержит кнопки для изменения состояния выбранных объектов:

В строке состояния можно изменять такие атрибуты схемы модели как тип шрифта, его размер, начертание (жирный шрифт, курсив, подчеркивание, перечеркивание), изменять характеристи­ки выбранных переменных, изменять цвет переменных, позицию текста в рабочей области, цвет стрелок, ширину стрелок, направ­ление стрелок и т.д.

Панель управления

С ее помощью меняются установки, управляющие действием Vensim. Панель управления открывается нажатием кнопки  или через пункт меню Windows. Панель управления в Vensim PLE имеет пять вкладок:

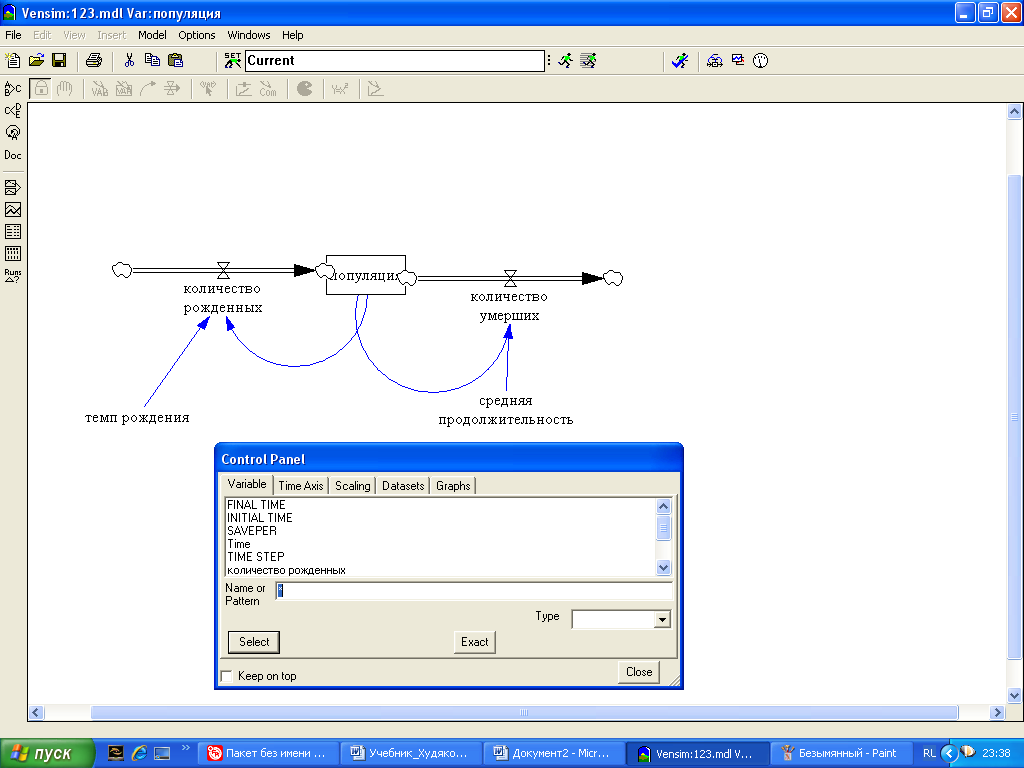
Variable позволяет выбрать переменные модели и устано­вить их тип.

Time Axis (ось времени) позволяет изменять горизонт мо­делирования (период моделирования) и шаг моделирования.

Scaling позволяет изменить масштабы выходных графов.

Datasets позволяет управлять созданными наборами данных. Graphs позволяет изменять и редактировать граф.

Задания к лабораторному занятию

Базовый уровень

Упражнение 1. Имитационная модель динамики численности населения региона. В качестве примера рассмотрим модель, приведенную в справочном разделе программы Vensim. Моделируется измене­ние численности населения региона. Если фиксировать числен­ность населения на начало каждого года, то она будет опреде­ляться как имеющееся количество на начало года плюс разница между родившимися за этот период и умершими:

Повышенный уровень

Циклы

Только переменные типов Auxiliary и Level имеют петли обратной связи (циклы), проходящие через них. Так, например, для более четкого представления, какие обратные связи имеет основная переменная Population, можно воспользоваться инст­рументом «Loops» . Окно результатов выглядит следующим образом (рис. 8).

 

Рисунок 8. Окно результатов при использовании инструмента «Loops»

 

Окно показывает, что у переменной Population существуют обратные связи с двумя переменными births и deaths, находящи­мися от этой переменной на расстоянии одной связи (длины).

Окно результатов, показывающее уравнение, лежащее в основе всех переменных в модели, единицы измерения для пе­ременных и введенные комментарии (если они были введены ранее) открывается при использовании инструмента анализа «Document» :

 

 

7. Вычислительный эксперимент.

Система Vensim позволяет сравнивать несколько вариан­тов выходных характеристик прогонов имитационных моделей, чтобы проследить динамику моделируемых событий при раз­личных вариантах (или стратегиях) развития. Исследователь может вводить различные значения переменных типа Constanta. Чтобы быстро найти эти переменные в модели в Vensim на ос­новной панели инструментов существует специальный инструмент - Set Up Simulation . При его активизации переменные типа Constanta появляются желтым текстом на синем фоне. Их значения можно менять, щелкнув по ним и изменив значение в EditBox и <Enter>. 

В рассматриваемой модели есть две такие переменные - birth rate и average lifetime. Изменим их значения. Для birth rate поставим 0,08 вместо 0,125, а для average lifetime поставим 65 лет вместо 70 лет. Осуществим прогон модели, результаты кото­рой запишется в новый файл Naselenl. Поскольку результаты предыдущих прогонов также сохраняются, то Граф-инструмент при его активизации строит два графика (рис. 9). Они показывают, что при сокращении рождаемости и уменьшении средней продолжительности жизни темп роста населения снижается.

 

Рисунок 9. Графическое отображение результатов моделирования

 

Инструмент анализа «Run Compare»  вносит в список все изменения констант:

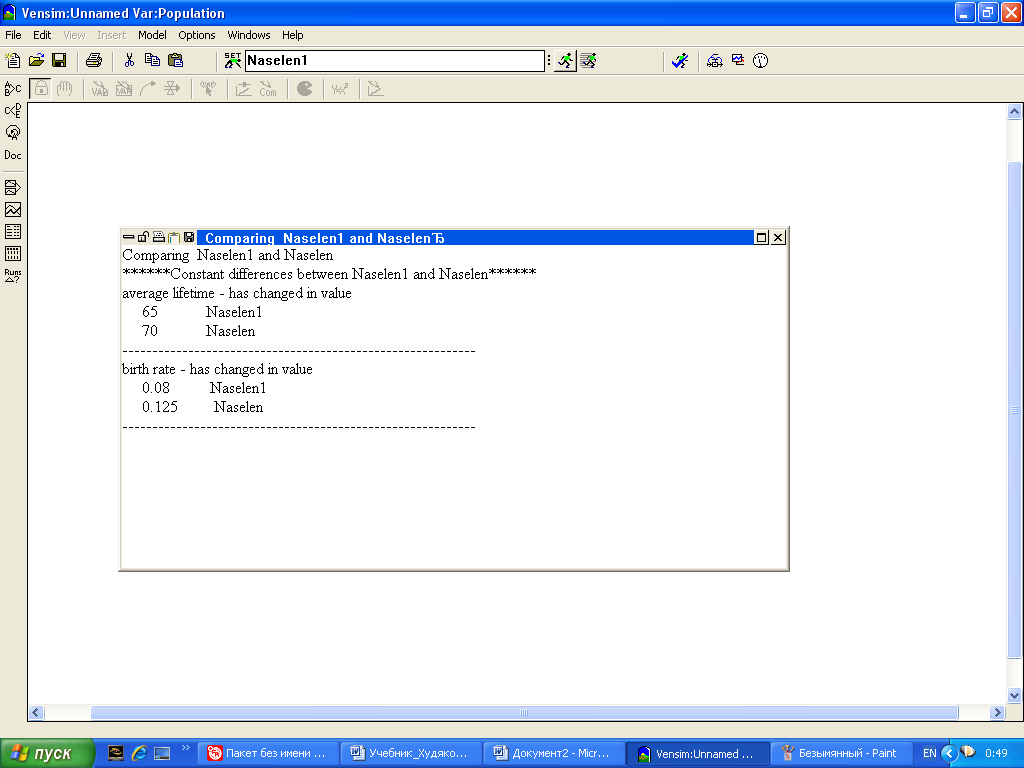
Граф позволяет проследить за изменением численности на­селения при указанных двух темпах рождаемости и средней продолжительности жизни.

 

Содержание отчета и его форма

Отчет к лабораторной работе оформляется в виде текстового документа по форме простого реферата и должен включать:

1. Название лабораторной работы.

2. Цель и содержание лабораторной работы.

3. Краткие выводы по результатам выполнения заданий к лабораторной работе.

4. Формулировку задания для самостоятельной работы и результат его выполнения.

Задания для самостоятельной работы

Базовый уровень

1. Основные инструменты создания и работы с имитационной моделью в Vensim PLE.

2. Охарактеризуйте средства построения схемы модели.

3. Этапы создания модели средствами системы Vensim PLE.

4. С какой целью в системе используется редактор выражений Equations?

5. Технология анализа результатов моделирования.

6. Технология проведения вычислительного эксперимента средствами системы Vensim PLE.

Повышенный уровень

7. Изменяя самостоятельно входные параметры модели, осуществите прогон полученной системы. Проанализируйте полученные результаты о том, что при увеличении/сокращении рождаемости и при увеличении/уменьшении средней продолжительности жизни темп роста населения снижается/увеличивается.

 

 

Лабораторная работа 8

Теоретическая часть

Система моделирования GPSS World поддерживает дискрет­но-событийный подход к имитационному моделированию. Дан­ную систему (как и примерно, около ста подобных систем, сущест­вующих сегодня на рынке) можно рассматривать как глобальную схему обработки заявок со стохастическими элементами (то есть систему массового обслуживания).

Типы операторов GPSS World

Операторы GPSS делятся на три типа:

1)  блоки;

2)  операторы описания данных;

3)  команды.

5.1. Для создания транзактов (заявок), входящих в модель, служит блок GENERATE (генерировать), имеющий следующий формат:

GENERATE A,B,C,D,E

В поле A задается среднее значение интервала времени между моментами поступления в модель двух последовательных транзактов. Если этот интервал постоянен, то поле B не используется. Если же интервал поступления является случайной величиной, то в поле B указывается модификатор среднего значения, который может быть задан в виде модификатора-интервала или модификатора-функции.

Модификатор-интервал используется, когда интервал поступления транзактов является случайной величиной с равномерным законом распределения вероятностей. В этом случае в поле B может быть задан любой стандартный числовой атрибут (СЧА), кроме ссылки на функцию, а диапазон изменения интервала поступления имеет границы A-B , A+B.

Ниже представлено графическое представление блока с обозначением операндов.

Например, блок

GENERATE 100,40

создает транзакты через случайные интервалы времени, равномерно распределенные на отрезке [60;140];

GENERATE 8

транзакт входит в модель через каждые 8 минут;

GENERATE 30,4„5

приход в модель через каждые 30 + 4 мин 5 транзактов;

GENERATE ,„5,2

приход в нулевой момент времени трех транзактов с приоритетом 2;

GENERATE 20,7,10„3

приход в модель через 20 ± 7 мин транзактов с приорите­том, более высоким, чем в примере № 4, причем первый транзакт приходит через 10 мин после начала работы системы.

Модификатор-функция используется, если закон распределения интервала поступления отличен от равномерного. В этом случае в поле B должна быть записана ссылка на функцию (ее СЧА), описывающую этот закон, и случайный интервал поступления определяется, как целая часть произведения поля A (среднего значения) на вычисленное значение функции.

В поле C задается момент поступления в модель первого транзакта. Если это поле пусто или равно 0, то момент появления первого транзакта определяется операндами A и B.

Поле D задает общее число транзактов, которое должно быть создано блоком GENERATE. Если это поле пусто, то блок генерирует неограниченное число транзактов до завершения моделирования.

В поле E задается приоритет, присваиваемый генерируемым транзактам. Число уровней приоритетов неограниченно, причем самый низкий приоритет - нулевой. Если поле E пусто, то генерируемые транзакты имеют нулевой приоритет.

Транзакты имеют ряд стандартных числовых атрибутов (СЧА). Например, СЧА с названием PR позволяет ссылаться на приоритет транзакта. СЧА с названием M1 содержит так называемое резидентное время транзакта, т.е. время, прошедшее с момента входа транзакта в модель через блок GENERATE. СЧА с названием XN1 содержит внутренний номер транзакта, который является уникальным и позволяет всегда отличить один транзакт от другого. В отличие от СЧА других объектов, СЧА транзактов не содержат ссылки на имя или номер транзакта. Ссылка на СЧА транзакта всегда относится к активному транзакту, т.е. транзакту, обрабатываемому в данный момент симулятором.

2. Для удаления транзактов из модели служит блок TERMINATE (завершить), имеющий следующий формат:

TERMINATE A

Значение поля A указывает, на сколько единиц уменьшается содержимое так называемого счетчика завершений при входе транзакта в данный блок TERMINATE. Если поле A не определено, то оно считается равным 0, и транзакты, проходящие через такой блок, не уменьшают содержимого счетчика завершений.

Графическое представление блока имеет вид:

Начальное значение счетчика завершений устанавливается управляющим оператором START (начать), предназначенным для запуска прогона модели. Поле A этого оператора содержит начальное значение счетчика завершений. Прогон модели заканчивается, когда содержимое счетчика завершений обращается в 0. Таким образом, в модели должен быть хотя бы один блок TERMINATE с непустым полем A, иначе процесс моделирования никогда не завершится.

Текущее значение счетчика завершений доступно программисту через системный СЧА TG1.

Участок блок-схемы модели, связанный с парой блоков GENERATE - ТERMINATE, называется сегментом. Простые модели могут состоять из одного сегмента, в сложных моделях может быть несколько сегментов.

Например, простейший сегмент модели, состоящий всего из двух блоков GENERATE и TERMINATE и в совокупности с управляющим оператором START моделирует процесс создания случайного потока транзактов, поступающих в модель со средним интервалом в 100 единиц модельного времени, и уничтожения этих транзактов. Начальное значение счетчика завершений равно 1000. Каждый транзакт, проходящий через блок TERMINATE, вычитает из счетчика единицу, и таким образом моделирование завершится, когда тысячный по счету транзакт войдет в блок TERMINATE. При этом точное значение таймера в момент завершения прогона непредсказуемо. Следовательно, в приведенном примере продолжительность прогона устанавливается не по модельному времени, а по количеству транзактов, прошедших через модель.

 

GENERATE 100,40

TERMINATE 1

START 1000

 

Если необходимо управлять продолжительностью прогона по модельному времени, то в модели используется специальный сегмент, называемый сегментом таймера.

 

GENERATE 100,40

TERMINATE

GENERATE 100000

TERMINATE 1

START 1

 

Например, в модели из двух сегментов, первый (основной) сегмент выполняет те же функции, что и в предыдущем примере. Заметим, однако, что поле A блока TERMINATE в первом сегменте пусто, т.е. уничтожаемые транзакты не уменьшают содержимого счетчика завершений. Во втором сегменте блок GENERATE создаст первый транзакт в момент модельного времени, равный 100000. Но этот транзакт окажется и последним в данном сегменте, так как, войдя в блок TERMINATE, он обратит в 0 содержимое счетчика завершений, установленное оператором START равным 1. Таким образом, в этой модели гарантируется завершение прогона в определенный момент модельного времени, а точное количество транзактов, прошедших через модель, непредсказуемо.

В приведенных примерах транзакты, входящие в модель через блок GENERATE, в тот же момент модельного времени уничтожались в блоке TERMINATE.

Замечание: Не путайте ограничитель транзактов в блоке GENERATE и счетчик завершения. Ограничитель задает число транзактов, которые войдут в модель, а счетчик – число транзактов, которые выйдут из модели. По окончании моделирования транзакты могут оставаться в модели. 

 

Задания к лабораторному занятию

Базовый уровень

Повышенный уровень

Упражнение 2. К компьютеру на обработку поступают задания. Из предварительного обследования получена информация, что интервал времени между двумя последовательными поступлениями заданий к компьютеру подчиняется равномерному закону распределения в интервале (1-11 мин.). Перед компьютером допустима очередь заданий, длина которой не ограничена. Время выполнения задания также равномерно распределено в интервале (1-19 мин.). Смоделировать обработку 100 заданий.

В среде GPSS программа, моделирующая работу вычислительной системы, выглядит следующим образом:

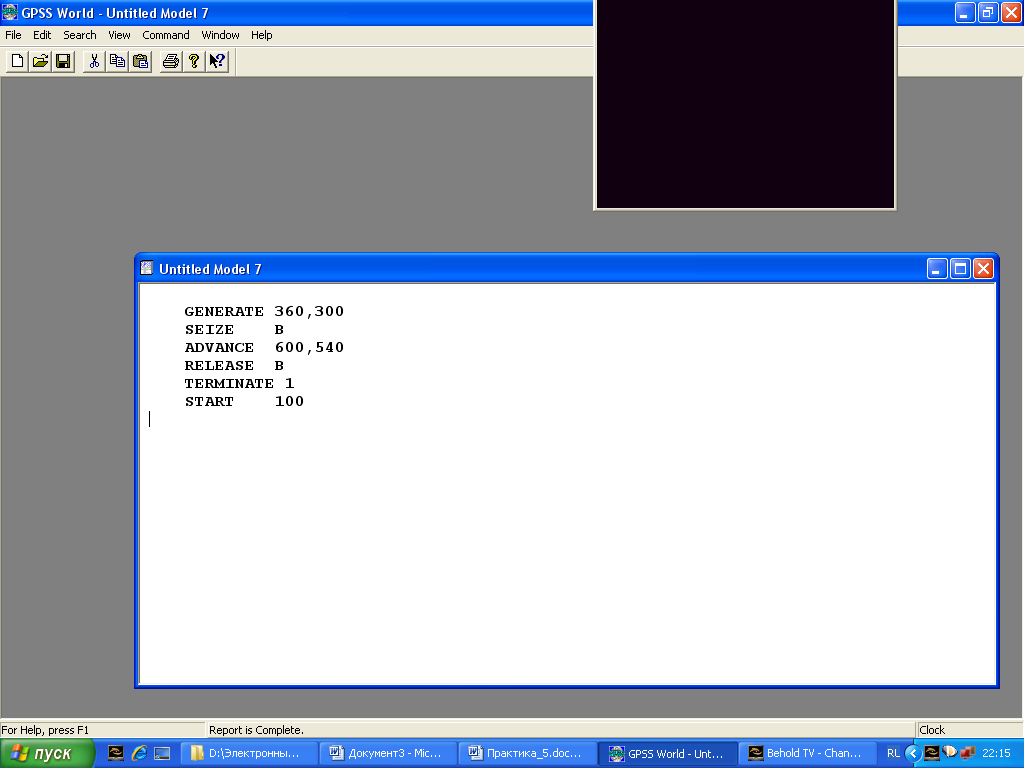
Содержание отчета и его форма

Отчет к лабораторной работе оформляется в виде текстового документа по форме простого реферата и должен включать:

1. Название лабораторной работы.

2. Цель и содержание лабораторной работы.

3. Краткие выводы по результатам выполнения заданий к лабораторной работе.

4. Формулировку задания для самостоятельной работы и результат его выполнения.

Задания для самостоятельной работы

Базовый уровень

1. Понятие системы массового обслуживания.

2. Охарактеризовать элементы СМО.

3. Характеристики СМО.

4. Основные характеристики работы СМО.

5. Характеристики сетей СМО.

6. Определение основных элементов языка GPSS.

7. Особенности работы с основными блоками GPSS: GENERATE,TERMINATE,START.

8. Назначение операторов QUEUE,DEPART.

Повышенный уровень

 

9. В набранной программе:

 

Внесите изменения, моделирующие работу вычислительного центра. Запустите и отладьте новые варианты программы:

1. К компьютеру на обработку поступают 14 заданий, интервал поступления заданий распределен по равномерному закону в диапазоне 3-11 мин.

2. К компьютеру на обработку в нулевой момент времени поступают 5 заданий с уровнем приоритета равным 25.

3. Задания поступают на обработку к компьютеру каждые 4-14 мин. Первое задание поступает на 20 минуте. Измените единицу модельного времени на 0,1 минуту.  

4. Моделирование заканчивается после того, как через модель пройдут 300 транзактов (заданий), транзакты должны поступать в модель каждые 1-11 минут.

5. Задайте время моделирования работы системы 8 часов, единица модельного времени – 1 секунда.

6. Как изменились характеристики работы моделируемой системы в результате внесенных изменений?

 

 

Лабораторная работа 9-10

Теоретическая часть

Устройства используются при моделировании систем для имитации работы оборудования единичной емкости, например, процессор, кана­л передачи данных, человек, компьютер. Устройство в любой момент времени может обрабатывать только одно сообщение (транзакт). Если в процесс обслуживания появляется новый транзакт, то он должен:

1. либо подождать своей очереди;
2. либо направиться в другое место;
3. либо прервать обслуживание текущего сообщения.

Для использования одноканального устройства транзакту необходимо выполнить следующие шаги.

-  ждать очереди, если необходимо;

-  когда подходит очередь занять устройство;

-  устройство находится в состоянии занятости, пока не закончится обслуживание, для обслуживания необходим некоторый интервал времени;

-  когда обслуживание закончится, освободить устройство.

Второй и четвертый шаги реализуются блоками SEIZE и RELEASE.

Блок SEIZE (занять) имеет следующий формат:

SEIZE A

Графическое представление блока имеет вид:

Свободный блок SEIZE позволяет вошедшему в него сообщению занять указанное устройство. Блок SEIZE задерживает сообщение, если устройство занято или находится в состоянии недоступнос­ти.

В поле А задается номер (имя) занимаемого устройства.

Сообщение, занявшее уст­ройство, затем пытается перейти к следующему по номеру блоку. Уст­ройство остается занятым до тех пор, пока занимающее его сообщение не войдет в соответствующий блок RELEASE. Прежде чем освободить устройство, сообщение может пройти через неограниченное число блоков.

Блок RELEASE (освободить) имеет следующий формат:

RELEASE A

Графическое представление блока имеет вид:

Блок RELEASE предназначен для освобождения устройства тем со­общением, которым в поле А задается номер (имя) освобождаемого уст­ройства.

Примеры:

1. Автомобиль занял бензиновую колонку (название колонки - Kol):

SEIZE Kol

2. Автомобиль освободил бензиновую колонку:

RELEASE Kol

Транзакты обслуживаются устройствами в течение некоторого промежутка времени. Для моделирования такого обслуживания, т.е. для задержки транзактов на определенный отрезок модельного времени (реализация шага 3), служит блок ADVANCE (задержать), имеющий следующий формат:

ADVANCE A,B

Операнды в полях A и B имеют тот же смысл, что и в соответствующих полях блока GENERATE. Следует отметить, что транзакты, входящие в блок ADVANCE, переводятся из списка текущих событий в список будущих событий, а по истечении вычисленного времени задержки возвращаются назад, в список текущих событий, и их продвижение по блок-схеме продолжается. Если вычисленное время задержки равно 0, то транзакт в тот же момент модельного времени переходит в следующий блок, оставаясь в списке текущих событий.

Графическое представление блока имеет вид:

 

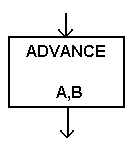
Примеры:

1. Клиент в банке обслуживается в среднем за 6 ± 2 минуты:

ADVANCE 6,2

2. Автомобиль занимает колонку Kol и заправляется в течение 2 мин, затем освобождает колонку (составить сегмент модели):

SEIZE Kol

...

ADVANCE 2

RELEASE Kol

 

3. Транзакты, поступающие в модель из блока GENERATE через случайные интервалы времени, имеющие равномерное распределение на отрезке [60;140], попадают в блок SEIZE и занимают устройство с номером 1. Далее в блоке ADVANCE определяется случайное время задержки транзакта, имеющее равномерное распределение на отрезке [30;130], и транзакт переводится в список будущих событий. По истечении времени задержки транзакт возвращается в список текущих событий и входит в блок RELEASE и освобождает устройство 1. Заметим, что в списке будущих событий, а значит и в блоке ADVANCE может одновременно находиться произвольное количество транзактов.

GENERATE 100,40

SEIZE 1

ADVANCE 80,50

RELEASE 1

 

В рассмотренных выше примерах случайные интервалы времени подчинялись равномерному закону распределения вероятностей. Для получения случайных величин с другими распределениями в GPSS используются вычислительные объекты: переменные и функции.

QUEUE Ochered ,3

2. Прибыв в банк, клиент встает в очередь (имя очереди Ochered). После того, как подойдет его очередь на обслуживание работником банка (имеющего имя Bankir), клиент, подходя к бан­киру, покидает очередь; расчеты с клиентом длятся 5 ± 2 минуты:

QUEUE Ochered
SEIZE Bankir

DEPART Ochered ADVANCE 5,2

RELEASE Bankir

Обозначения в стандартном отчете со статистикой очереди озна­чают следующее:

QUEUE	МАХ	CONT.	ENTRY	ENTRY(0)	AVE. CONT.	AVE.TIME	AVE.(-0)	RETRY
Назва- ние очереди сим- вольное или чи­словое)	Макси- мальная длина очереди	Текущая длина очереди	Общее кол-во входов	Кол-во нулевых входов	Средняя длина очереди	Среднее время пребыва- ния транзакта в очереди	Среднее время пребыва- ния транзакта в очереди без учета нулевых входов	Кол-во ожидающих транзактов

 

Знание приведенных выше блоков достаточно для построе­ния простой имитационной модели.

 

Задания к лабораторному занятию

Базовый уровень

Упражнение 1. Наберите следующий код GPSS.

   

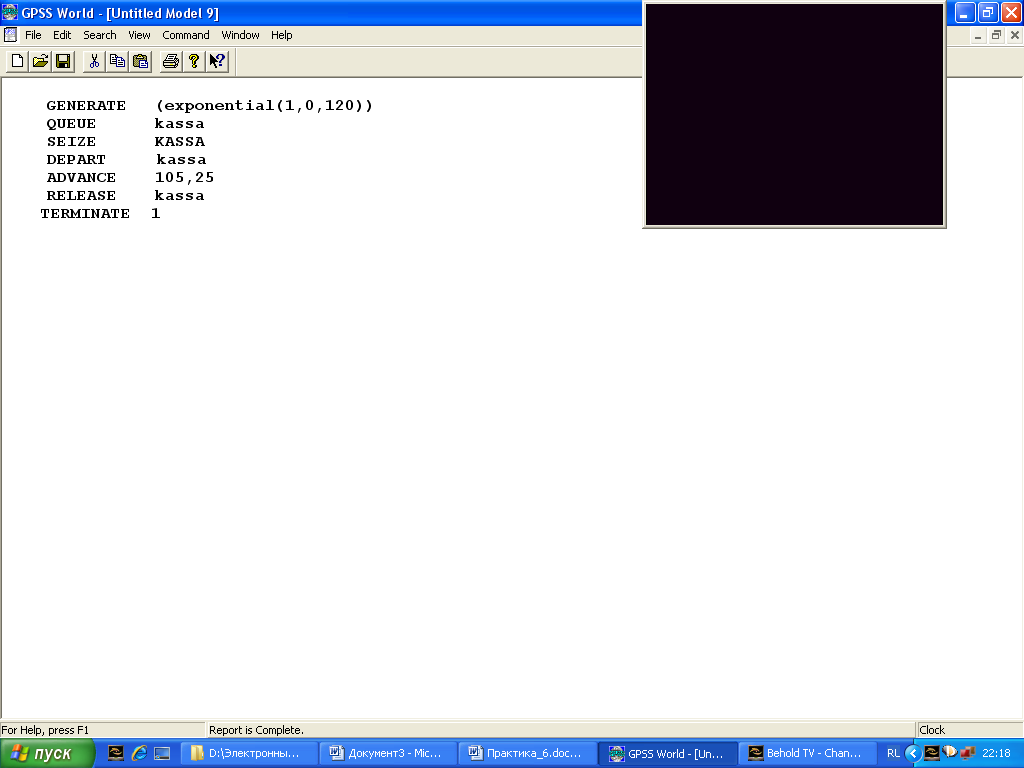
Откомпилируйте модель. Запустите ее на выполнение, задав в диалоговом окно Start Command - 1000 вместо 1.

Одновременно, по результатам моделирования будет создано окно итоговой статистики (REPORT), где будет собрана вся стандартная статистика по работе модели. Она будет выглядеть примерно следующим образом.

 

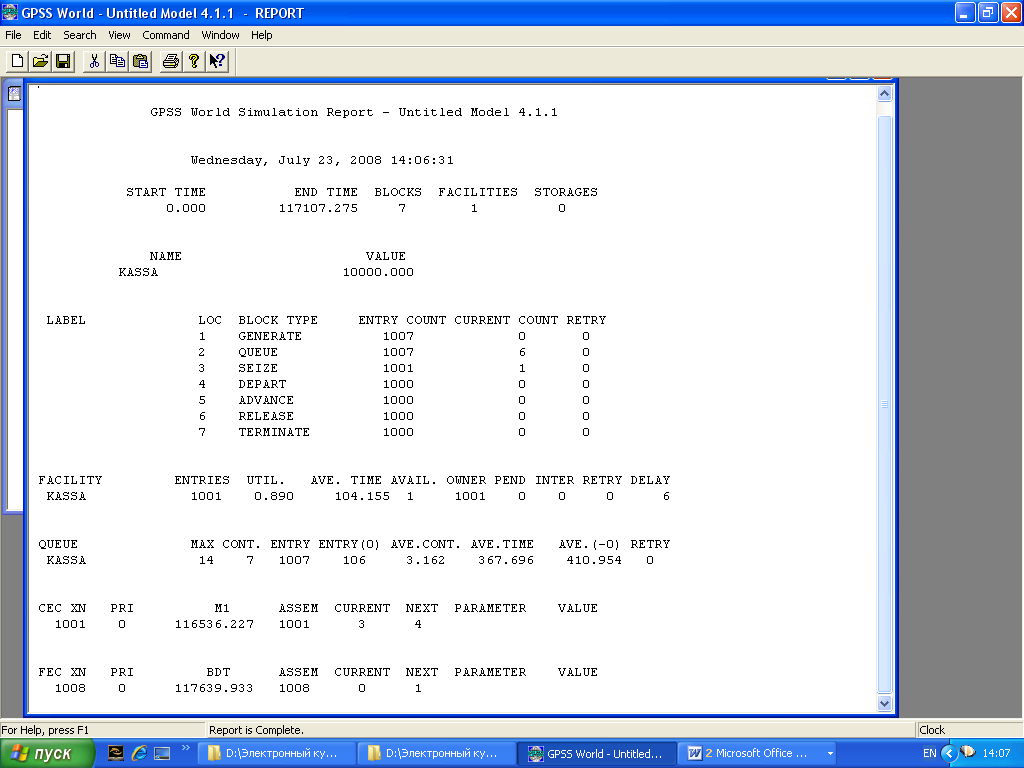
Обсудим как саму модель, так и полученные результаты.

QUEUE kassa

Эта строка моделирует поступление клиентов в очередь, с тем, чтобы можно было собрать статистику по очереди к кассе (kassa)

SEIZE kassa

Эта строка моделирует начало работы кассира с клиентом. Клиент может попасть на обслуживание к кассиру, только тогда, когда кассир обслужит клиентов пришедших раньше. Когда с клиентом началась работа, кассир считается занятым.

DEPART kassa       

Эта строка моделирует удаление клиента из очереди, так как он уже обслуживается у кассира. Если использовался блок QUEUE, то должен использоваться и блок DEPART. Только тогда будет собрана правильная статистика по очереди.

ADVANCE 105,25

Эта строка моделирует задержку клиента на обслуживание у кассира. Средний интервал задержки равен 105 секундам модельного времени, а отклонение интервала от среднего составляет по 25 модельных секунд в обе стороны. Любое значение времени задержки из этого интервал абсолютно равновероятно.

RELEASE kassa

Эта строка моделирует завершение работы кассира с клиентом. После этого, кассир вновь становится свободным и может начать обслуживание следующего клиента (если он есть).

TERMINATE 1        

Эта строка моделирует уход клиента из системы. А число 1 в ней обеспечивает завершение моделирования после того, как будет обслужено то число клиентов, которое указано в Start (то есть 1000).

Анализируя выходную статистику, можно определить следующие результаты моделирования. На обслуживание 1000 клиентов системе понадобилось 117107.275 секунд модельного времени. Всего поступило на обслуживание 1007 клиентов. Кассир был занят на 89%. Среднее время обслуживания клиента составило 104.155 секунды. Максимальная величина очереди составила 14 клиентов. 106 клиентов вообще не стояли в очереди. Средняя величина очереди была 3.162. А среднее время, которое клиент провёл в очереди, равно 367.696 секунд.

Общий вывод – при такой скорости работы, система не очень хорошо справляется с работой, что может привести к потере клиентов. После нескольких экспериментов с различными временами обслуживания, нетрудно установить, что заменив блок ADVANCE на ADVANCE 80,25, мы получим следующие результаты.

Средняя занятость кассира - 0.678. Среднее время обслуживания - 79.609, Средняя длина очереди - 0.644. Среднее время в очереди - 75.504 , что уже гораздо лучше.

Чтобы посмотреть, как себя ведёт, например, очередь к кассе в процессе моделирования, то, вызвав пункт меню Window/ Simulation Window/ Plot Window… В полученном окне надо заполнить поля в New Expression и щёлкнуть по Plot. Затем в Window Contents заполнить поля, как указано в окне. Затем щелкнуть по OK.

 

Тогда после запуска модели по Start 1000, получим следующее окно, отображающее изменение очереди к кассиру во времени.

 

Повышенный уровень

Упражнение 2. Смоделировать работу цеха по стрижке овец в течение рабо­чей смены (480 мин.), если овцы поступают в цех равномерно ка­ждые 5 ± 2 мин. В цехе работает один работник, который стрижет одну овцу в среднем за 7 ± 3 минуты.

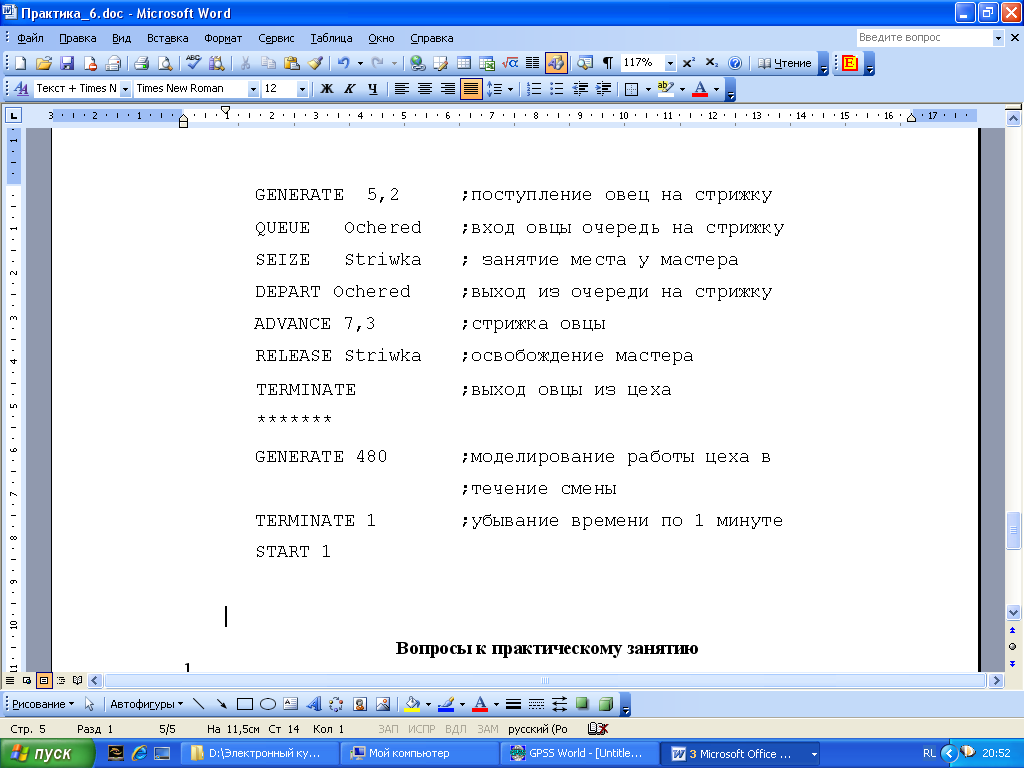
В результате выполнения программы моделирования получите отчет и проанализируйте характеристики работы цеха.

Содержание отчета и его форма

Отчет к лабораторной работе оформляется в виде текстового документа по форме простого реферата и должен включать:

1. Название лабораторной работы.

2. Цель и содержание лабораторной работы.

3. Краткие выводы по результатам выполнения заданий к лабораторной работе.

4. Формулировку задания для самостоятельной работы и результат его выполнения.

Задания для самостоятельной работы

Базовый уровень

1. Особенности работы с основными блоками GPSS: SEIZE , RELEASE ,ADVANCE, QUEUE,DEPART.

2. Охарактеризуйте обозначения в стандартном отчете со статистикой очереди.

 

Повышенный уровень

3. Приведите фрагмент программы, который моделирует обработку детали на станке. Название устройства – MACHINE, время обработки – 10 ед. модельного времени.

4. Напишите сегмент программы, который описывает процесс шлифования изделия. Шлифование занимает 3-5 минут, в каждый момент времени может обрабатываться только одно изделие. Единица модельного времени – 1 секунда.

5. Увеличьте (уменьшите) на три единицы длину очереди с номером 3;

6. Обнулите длину очереди QPR.

   

Лабораторная работа 11-12

Теоретическая часть

Устройство в GPSS используют для моделирования одиночного устройства обслуживания. Два или более обслуживающих устройств, работающих параллельно, могут моделироваться двумя или более одинаковыми устройствами. Это необходимо, когда устройства являются разнородными.

Если параллельно работающие устройства являются одинаковыми, то для их моделирования может использоваться объект многоканальное устройство (МКУ).

Количество устройств, которое моделирует МКУ задает пользователь с помощью оператора STORAGE .

Формат оператора:

Метка STORAGE А

где Метка – имя МКУ;

А – емкость МКУ (количество однотипных устройств, входящих в МКУ).

Блок ENTER имеет следующий формат записи:

ENTER A,[B]

Графическое изображение блока:

Блок ENTER позволяет вошедшему сообщению (транзакту) использовать много­канальное устройство. Сообщение может быть задержано на входе в блок, если многоканальное устройство заполнено или имеющейся емкос­ти недостаточно или устройство в данный момент недоступно.

В поле А указывается номер или имя многоканального устройст­ва, куда входит сообщение.

В поле В содержится число занимаемых единиц многоканального устройства. Если поле В пусто, то предполагается что занимается од­на единица. Если это значение равно нулю, то сообщение никогда не задерживается на входе, а блок рассматривается как нерабочий.

Активное сообщение не может войти в блок ENTER, если запрос на многоканальное устройство не может быть удовлетворен.

Активное сообщение не может войти в блок ENTER, если многока­нальное устройство находится в недоступном состоянии.

Когда сообщение входит в блок ENTER, то операнд А использует­ся для нахождения многоканального устройства с указанным именем. Если такое многоканальное устройство не существует, то возникает ошибка выполнения. В противном случае используется операнд В для оценки емкости многоканального устройства.

Одно и то же сообщение может входить в неограниченное число многоканальных устройств, а впоследствии освобождать их (или часть из них).

Блок LEAVE имеет следующий формат:

LEAVE A,[B]

Графическое изображение блока:

Блок LEAVE освобождает определенное число единиц многоканаль­ного устройства. Занятый объем многоканального устройства уменьшается на число освобождаемых единиц. Оставшаяся емкость многоканального устройства увеличивается на ту же величину. Счетчик числа входов не изменяет­ся.

Поле А блока LEAVE определяет номер или имя многокального ус­тройства.

Поле В - число освобождаемых единиц многоканального устройст­ва. Если это поле пусто, предполагается 1. Число осво­бождаемых единиц не должно превышать текущее содержимое многоканального устройства.

С многоканальными устройствами связаны следующие СЧА:

Sномер или S$имя - текущее число занятых каналов в многоканальном устройстве. Величина изменяется блоками ENTER и LEAVE. Например, S$OPER - текущее число занятых каналов многоканального уст­ройства OPER;

Rномер или R$имя - число свободных каналов многоканального устройства. Эта величина также изменяется блоками ENTER и LEAVE. Например, R$MACH - свободный объем многоканального устройства MACH;

SRномер или SR$имя - коэффициент использования многоканального устройства в тысячных долях, т.е., если коэффициент равен 0.65, то SR равно 650;

SAномер или SA$имя - среднее содержимое многоканального устройства;

SMномер или SM$имя - максимальное содержимое многоканального устройства;

SCномер или SC$имя  - общее число входов в многоканальное устройство;

STномер или ST$имя - среднее время пребывания одной заявки в многоканальном устройстве.

S Eномер или SE$имя - флаг не занятости (пустоты) многоканального устройства: 1 - свободно, 0 - занято;

SFномер или SF$имя - флаг занятости всех каналов многоканального устройства: 1 - заполнено, 0 - не заполнено;

SVномер или SV$имя - флаг готовности многоканального устройства: 1 - готово, 0 - не готово;

Для своего обслуживания, заявка может одновременно занимать любое число одноканальных и многоканальных устройств.

XFER TRANSFER ,NEXT

NEXT SEIZE 1

 

Сообщения, входящие в блок TRANSFER XFER, переходят к блоку NEXT.

TRANSFER , V$TER

Сообщения, которые входят в вышеприведенный блок TRANSFER, сразу переходят в блок, номер которого определяется переменной TЕR.

Статистический режим выбора

Когда операнд А не является зарезервированным словом, блок TRANSFER работает в статистическом режиме выбора.

Значение аргумента, записанного после точки (.) в поле А, рассматривается как трехзначное число, показывающее (в частях от тысячи), какой процент входящих в блок сообщений следует направить к блоку, указанному в поле С. Остальные сообщения направляются к блоку, указанному в поле В, или к следующему по номеру блоку, если операнд В пропущен. Для каждого сообщения выбирается один из двух возможных вариантов; после того как выбор сделан, второй вариант для этого сообщения не рассматривается.

Числовое значение может быть задано при помощи любого стандартного числового атрибута. Если вычисленное значение аргумента меньше или равно нулю, будет происходить безусловная передача сообщений к блоку, указанному в поле В. Если же значение аргумента больше или равно 1000, то будет происходить безусловная передача сообщений к блоку, указанному в поле С.

Например,

TRANSFER BOTH, TRY1, TRY2

TRY1 SEIZE 1

TRY2 SEIZE 2

     

Режим ALL

Если в поле А стоит зарезервированное слово ALL, блок TRANSFER работает в режиме ALL.

В этом режиме каждое входящее сообщение прежде всего пытается перейти к блоку, указанному в поле В. Если сообщение в этот блок войти не может, то последовательно проверяются все блоки в определенном ряду в поисках первого, способного принять это сообщение, включая блок, указанный операндом С. Номер каждого проверяемого блока вычисляется как сумма номера предыдущего блока и шага, заданного операндом D:

N + M, N + 2M, N + 3M, ... L,

где N - номер блока, указанного в поле В;

М - значение шага, заданного в поле D;

       L - номер блока, указанного в поле С.

Этот номер должен быть больше номера блока, указанного в поле В, на величину, кратную шагу М. Если операнд D не задан, то проверяется каждый блок, номер которого принадлежит этому ряду, включая блок, определенный операндом С . Блоки, номера которых выше номера блока, указанного в поле С, не проверяются. Как только первый блок, способный принять сообщение, будет найден, сообщение входит в этот блок и оттуда продолжает свое дальнейшее движение. Если сообщение не может перейти ни к одному из указанных блоков, оно остается в блоке TRANSFER и повторяет описанную выше процедуру при каждом просмотре списка текущих событий до тех пор, пока не выйдет из блока.

Поскольку обычно в полях В и С записываются символические метки блоков, блоки следует располагать таким образом, чтобы при присвоении номеров разность между номерами блоков, указанных в полях В и С, была кратна шагу, указанному в поле D.

Например,

TRANSFER ALL, 60, 120, 10

В этом примере сообщение будет последовательно пытаться перейти к блокам 60, 70, 80, ... 120.

TRANSFER ALL, 60, 120, 25

В данном примере режим ALL недопустим, потому что разность между номерами блоков, записанных в полях В и С, не является кратной шагу, указанному в поле D.

Условными являются только режимы BOTH и ALL. Во всех остальных режимах выбор следующего блока производится в момент входа сообщения в блок. В режимах BOTH и АLL выбор следующего блока производится в момент снятия блокирующего условия. Следует отметить, что каждый раз, когда интерпретатор при просмотре списка текущих событий обнаруживает сообщение, задержанное в блоках TRANSFER BOTH или TRANSFER ALL, он пытается продвинуть сообщение, начиная с блока, указанного в поле В. Следовательно, в режиме BOTH в тех случаях, когда возможен переход к обоим блокам (В и С), блок В имеет некоторое преимущество. Аналогично, в режиме ALL в случае, когда возможен переход к нескольким блокам, блоки с меньшими номерами имеют некоторое преимущество перед блоками с большими номерами.

Режим PICK

Если в поле А стоит зарезервированное слово PICK, блок TRANSFER работает в режиме PICK. В этом режиме из последовательности блоков с номерами N, N+1, N+2,...M (N - номер блока, указанного поле В, а М - номер блока, указанного в поле С) случайным образом выбирается один блок, к которому должно быть направлено сообщение.

Все блоки, включая указанные в полях В и С, выбираются с одинаковой вероятностью, равной 1/(М-N)+1. Сообщение пытается перейти только к выбранному для него блоку. Если сообщение не может сразу перейти к следующему блоку, то оно будет ждать в блоке TRANSFER до тех пор, пока не будет снято блокирующее условие. Номер блока в поле С должен быть больше или равен N+1.

Например,

TRANSFER PICK,30,39

Сообщение, вошедшее в блок TRANSFER, пытается войти в один из 10 блоков (30,31,...39) с равной вероятностью: 1/10.

Помимо блока TRANSFER, потоком сообщений может управлять блок TEST.

Блок TEST имеет следующий формат:

TEST < X > < A >,< B >,[< C >]

Графическое представление блока (в безусловном режиме):

Определяет номер следующего блока для вошедшего в него сообщения в зависимости от того, выполняется требуемое условие или нет. Блок управляет потоком сообщений, проверяя выполнение алгебраических отношений между значениями СЧА, заданных в полях А и В.

Операнды А и В - сравниваемые величины, которые могут быть именем, любым целым числом, СЧА или СЧА*<параметр>.

Во вспомогательном поле операции оператора описания блока TEST - <X> - записывается один из шести условных операторов:

– 'L' - меньше. Отношение истинное, если значение аргумента поля А меньше значения аргумента поля В;

– 'LE' - меньше или равно

– 'E' - равно.

– 'NE' - не равно.

– 'G' - больше.

– 'GE' - больше или равно.

Если отношение СЧА, заданных в полях А и В, истинно, сообщение переходит к следующему блоку. Если отношение ложно, сообщение переходит к блоку, номер которого задан полем С.

C - номер блока для входящего сообщения, если отношение величин, заданных в полях А и В, ложно. Операнд C может быть именем, положительным целым числом, СЧА или СЧА*<параметр>.

Пример.

TEST G M1,500,SSS

SEIZE 1

…

SSS SEIZE 2

…

                        

Если значение времени пребывания транзакта в модели больше 500, то переходим к следующему по номеру блоку,  ложно к метке SSS.

SPLIT 2,MET,1

Создаются две копии, которые передаются по метке MET. Номер копии записан в параметре P1.

     

Блок ASSEMBLE имеет следующий формат:

ASSEMBLE <A>

Графическое изображение блока:

Блок ASSEMBLE объединяет заданное число сообщений, принадлежащих к одному семейству, в одно сообщение (т.е. осуществляет сборку заданного числа сообщений). После сборки из блока ASSEMBLE выходит только одно сообщение, которое переходит в следующий по номеру блок. В одном и том же блоке ASSEMBLE возможна одновременная сборка сообщений нескольких семейств. Когда сообщение входит в блок ASSEMBLE, интерпретатор просматривает семейство, к которому принадлежит это сообщение, и проверяет, есть ли другое сообщение из того же семейства в данном блоке ASSEMBLE. Поле А задает число сообщений, участвующих в сборке. Операнд А может быть именем, положительным целым, СЧА, СЧА*<параметр>.

 

Блок MATCH имеет следующий формат:

MATCH <A>

Графическое изображение блока:

Блок MATCH используется для синхронизации движения двух сообщений, принадлежащих к одному семейству, без удаления этих сообщений из модели.

Блоки MATCH не объединяют синхронизируемые сообщения. Синхронизация осуществляется путем подбора пар сообщений из одного семейства и задержки этих сообщений до тех пор, пока оба сообщения из одной пары не поступят в заданные точки модели. Сообщения никогда не задерживаются в блоке MATCH. Сообщения, для которых выполнилось условие синхронизации, переходят к следующему по номеру блоку. В одной паре блоков MATCH могут одновременно находиться в состоянии синхронизации пары сообщений из различных семейств. Возможна также одновременная синхронизации пар сообщений из одного семейства в нескольких блоках MATCH.

Поле А задает имя или номер другого блока MATCH, называемого "сопряженным блоком MATCH". Если такого блока нет, происходит останов по ошибке. Операнд А может быть именем, положительным целым, СЧА, СЧА*<параметр>.

Задания к лабораторному занятию

Базовый уровень

Упражнение 1. Изменим условие задачи о работе вычислительного центра. Пусть в вычислительной системе два компьютера (интенсивность обработки заданий одинаковая), все остальные условия остаются без изменений.

В среде GPSS программа, моделирующая работу вычислительной системы, выглядит следующим образом:

                  

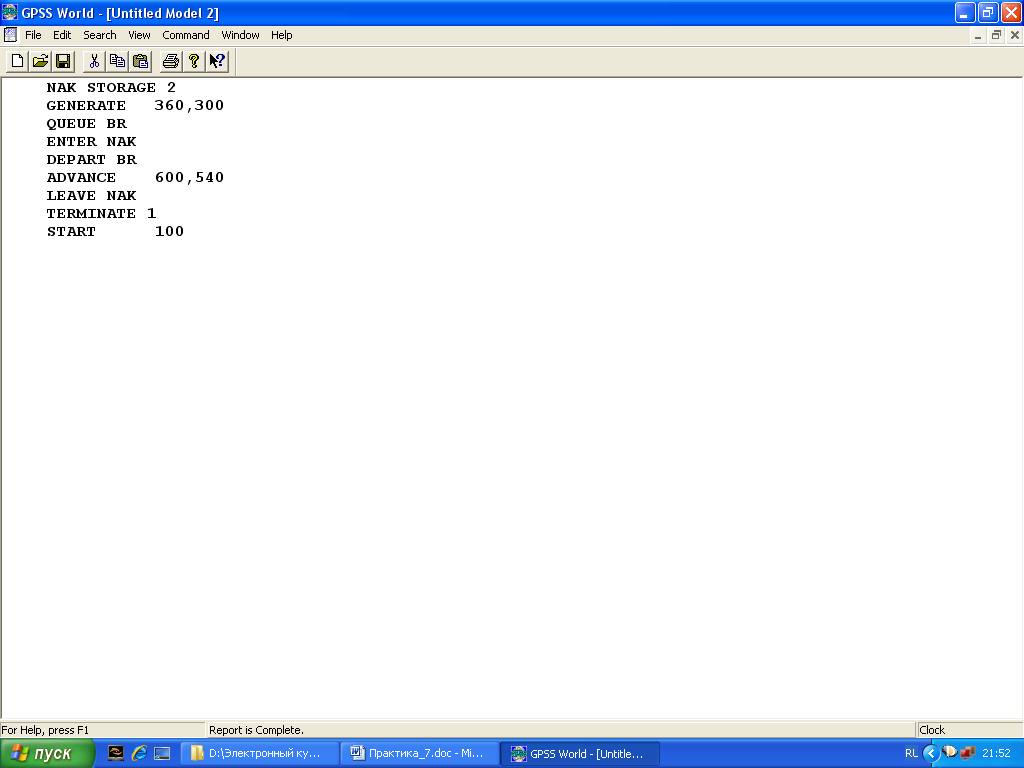
Обратите внимание, в программе появилась дополнительная строка NAK STORAGE 2.

И блоки SEIZE – RELEASE заменены соответственно на блоки ENTER – LEAVE, моделирующие работу с многоканальным устройством.

В результате выполнения программы моделирования работы вычислительной системы с двумя компьютерами GPSS выдаст отчет с информацией об использовании МКУ:

STORAGE – имя МКУ

CAP. – емкость МКУ, заданную оператором STORAGE

REM. – количество единиц свободной емкости в конце периода моделирования

MIN. – минимальное количество емкости за используемый период

MAX. - максимальное количество емкости за используемый период

ENTRIES – количество входов в МКУ за период моделирования

AVL . – состояние готовности МКУ в конце периода моделирования (1 – МКУ готов, 0 – нет)

AVE . C . – среднее значение занятой емкости за период моделирования

UTIL. – средний коэффициент использования всех устройств МКУ

RETRY – количество транзактов, ожидающих специальных условий, зависящих от состояния МКУ

DELAY – определяет количество транзактов, ожидающих занятия или освобождения устройства МКУ

Упражнение 2. Сравните отчеты по результатам моделирования работы вычислительной системы с одним компьютером и с двумя. Какие показатели изменились и как? Какой вариант организации работы вычислительной системы более предпочтителен?

Упражнение 3. Простейший пример применения многоканальных и одноканальных устройств совместно:

Пусть заявки первого типа поступают на обслуживание в систему с интервалом 100±50 секунд. Они проходят вначале через 5 канальное устройство nac, где обслуживаются в течение 450± 100 сек. А затем они проходят через одноканальное устройство 3, где обслуживаются в течение 90± 20 сек и покидают модель.

 Пусть также заявки второго типа поступают на обслуживание в систему с интервалом 1000±100 секунд. Они проходят через 5 канальное устройство nac, где обслуживаются в течение 500± 200 сек, занимая по 2 канала. Затем они покидают модель. Промоделировать обслуживание 1000 заявок. Текст такой модели, мог бы иметь, например, следующий вид:

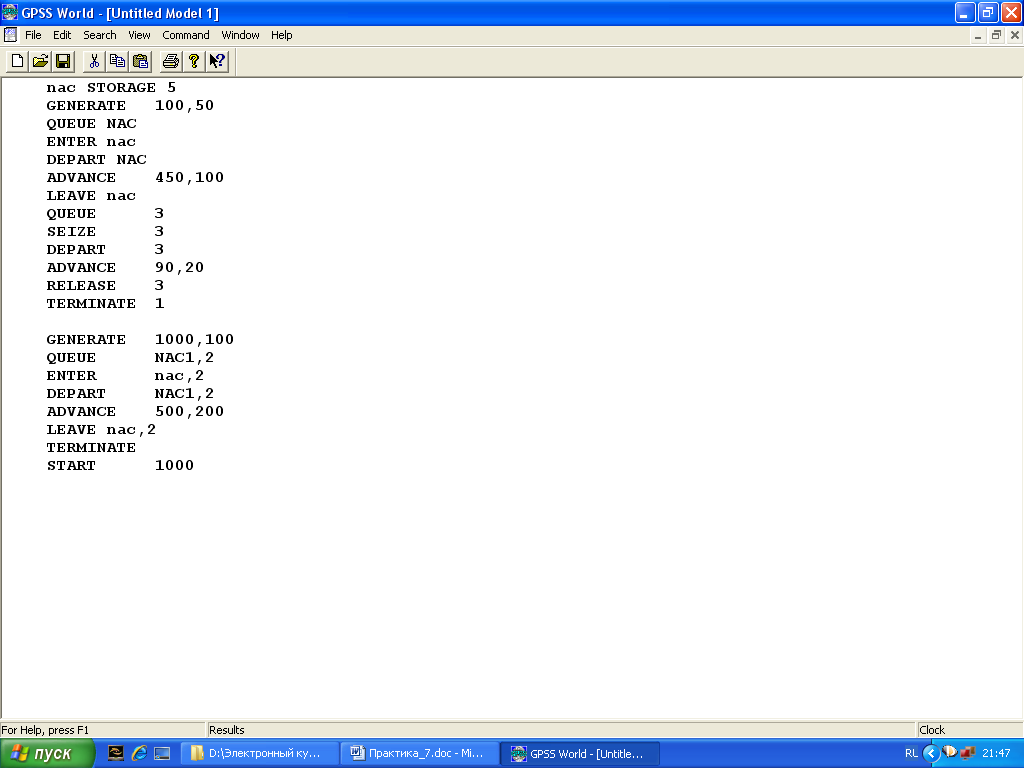
Результаты моделирования могут выглядеть, например, следующим образом:

 

         GPSS World Simulation Report - Untitled Model 1.3.1

 

               Saturday, July 26, 2008 20:45:33 

 

      START TIME      END TIME BLOCKS FACILITIES STORAGES

           0.000    100249.641 19   1     1

 

         NAME                  VALUE 

     NAC                    10000.000

     NAC1                   10001.000

 

 LABEL         LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY

               1 GENERATE     1008        0  0

               2 QUEUE        1008        0  0

               3 ENTER        1008        0  0

               4 DEPART       1008        0  0

               5 ADVANCE      1008        5  0

               6 LEAVE        1003        0  0

               7 QUEUE        1003        2  0

               8 SEIZE        1001        1  0

               9 DEPART       1000        0  0

              10    ADVANCE      1000        0  0

              11 RELEASE      1000        0  0

              12 TERMINATE    1000        0  0

              13 GENERATE      101        0  0

              14 QUEUE         101       53  0

              15 ENTER          48        0  0

              16 DEPART         48        0  0

              17 ADVANCE        48        0  0

              18 LEAVE          48        0  0

              19 TERMINATE      48        0  0

 

FACILITY    ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY

 3            1001 0.899 90.014 1 1103 0 0 0 2

 

QUEUE         MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY

 3              6 3 1003 132 1.922 192.076 221.186 0

 NAC           51 0 1008 26 18.775 1867.280 1916.719 0

 NAC1         106 106 202 0 36.816 18271.466 18271.466 0

 

STORAGE       CAP. REM. MIN. MAX. ENTRIES AVL. AVE.C. UTIL. RETRY DELAY

 NAC            5 0 0 5 1104 1 4.972 0.994 0 53

 

CEC XN PRI     M1 ASSEM CURRENT NEXT PARAMETER VALUE

1103 0  99559.739 1103 8 9

 

FEC XN PRI    BDT ASSEM CURRENT NEXT PARAMETER VALUE

1111 0 100267.030 1111 0 1

1104 0 100271.944 1104 5 6

1106 0 100273.148 1106 5 6

1109 0 100440.757 1109 5 6

1107 0 100582.197 1107 5 6

1110 0 100643.369 1110 5 6

1108 0 100899.989 1108 0 13

 

Однако, если ввести последовательно команды

Nac storage 7

Clear

Start 1000

 

То получим следующую выходную статистику, в которой емкость многоканального устройства будет уже 7, а очереди к устройствам окажутся заметно меньше.

 

         GPSS World Simulation Report - Untitled Model 1.3.2

 

               Saturday, July 26, 2008 20:47:33 

 

      START TIME      END TIME BLOCKS FACILITIES STORAGES

           0.000       101882.427 19   1     1

 

         NAME                  VALUE 

     NAC                    10000.000

     NAC1                   10001.000

 

 LABEL         LOC BLOCK TYPE ENTRY COUNT CURRENT COUNT RETRY

               1 GENERATE     1006        0  0

               2 QUEUE        1006        0  0

               3 ENTER        1006        0  0

               4 DEPART       1006        0  0

               5 ADVANCE      1006        6  0

               6 LEAVE        1000        0  0

               7 QUEUE        1000        0  0

               8 SEIZE        1000        0  0

               9 DEPART       1000        0  0

              10 ADVANCE      1000        0  0

              11 RELEASE      1000        0  0

              12 TERMINATE    1000        0  0

              13 GENERATE      101        0  0

              14 QUEUE         101        0  0

              15 ENTER         101        0  0

              16 DEPART        101        0  0

              17    ADVANCE       101        0  0

              18 LEAVE         101        0  0

              19 TERMINATE     101        0  0

 

FACILITY    ENTRIES UTIL. AVE. TIME AVAIL. OWNER PEND INTER RETRY DELAY

 3            1000 0.884 90.056 1   0 0 0 0 0

 

QUEUE         MAX CONT. ENTRY ENTRY(0) AVE.CONT. AVE.TIME AVE.(-0) RETRY

 3              4 0 1000 252 0.570 58.023 77.571 0

 NAC            2 0 1006 875 0.057 5.743 44.100 0

 NAC1           2 0 202 178 0.016 8.304 69.896 0

 

 

STORAGE       CAP. REM. MIN. MAX. ENTRIES AVL. AVE.C. UTIL. RETRY DELAY

 NAC            7    1 0 7 1208 1 5.418 0.774 0 0

 

FEC XN PRI    BDT ASSEM CURRENT NEXT PARAMETER VALUE

1105 0 101945.426 1105 5 6

1102 0 101970.637 1102 5 6

1109 0 101993.030 1109 0 1

1104 0 102042.379 1104 5 6

1106 0 102197.803 1106 5 6

1108 0 102221.671 1108 5 6

1107 0 102279.501 1107 5 6

1103 0 102338.769 1103 0 13

Повышенный уровень

Упражнение 4 . В СМО поступают заявки по равномерному закону в интервале (3,7) минут. Для каждой заявки создается одна копия. Заявка и копия проходят параллельную обработку в двух каналах обслуживания с одинаковой интенсивностью обслуживания (4,8) мин. После обработки заявка и копия собираются в один пакет и выводятся из системы. Смоделировать работу системы по обработке 100 пакетов.

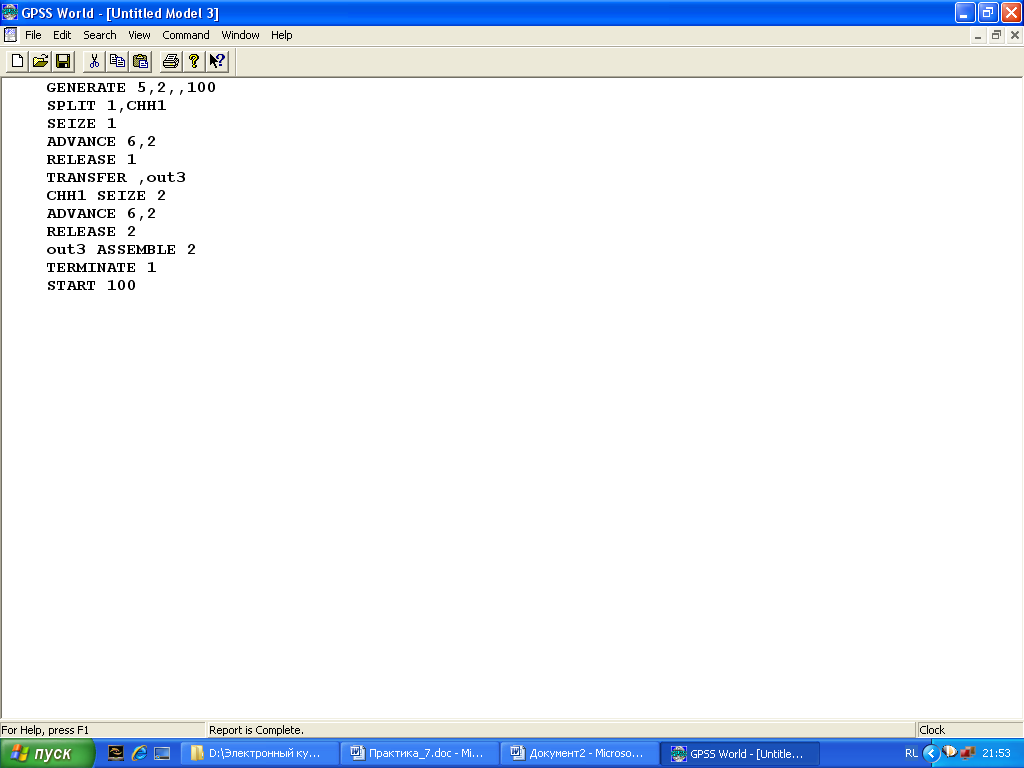
Блок SPLIT создает одну копию транзакта и направляет ее по метке CHH 1 на блок SEIZE 2. При этом через блок SPLIT проходит транзакт-родитель на следующий по номеру блок. В блоке ASSEMBLE собираются два транзакта, а выходит из него только один. За полный цикл моделирования в блоке ASSEMBLE собираются 200 транзактов, а выходит из него только 100 транзактов. Формально блок ASSEMBLE уничтожает 100 транзактов.

 Упражнение 5. В СМО поступают заявки по равномерному закону в интервале (3,7) минут. Для каждой заявки создается одна копия. Заявка и копия проходят параллельную обработку в двух каналах обслуживания с одинаковой интенсивностью обслуживания (4,8) мин. После обработки заявка и копия собираются в один пакет, который обслуживается третьим каналом с интенсивностью (5,7) минут. Смоделировать работу системы по обработке 100 пакетов.

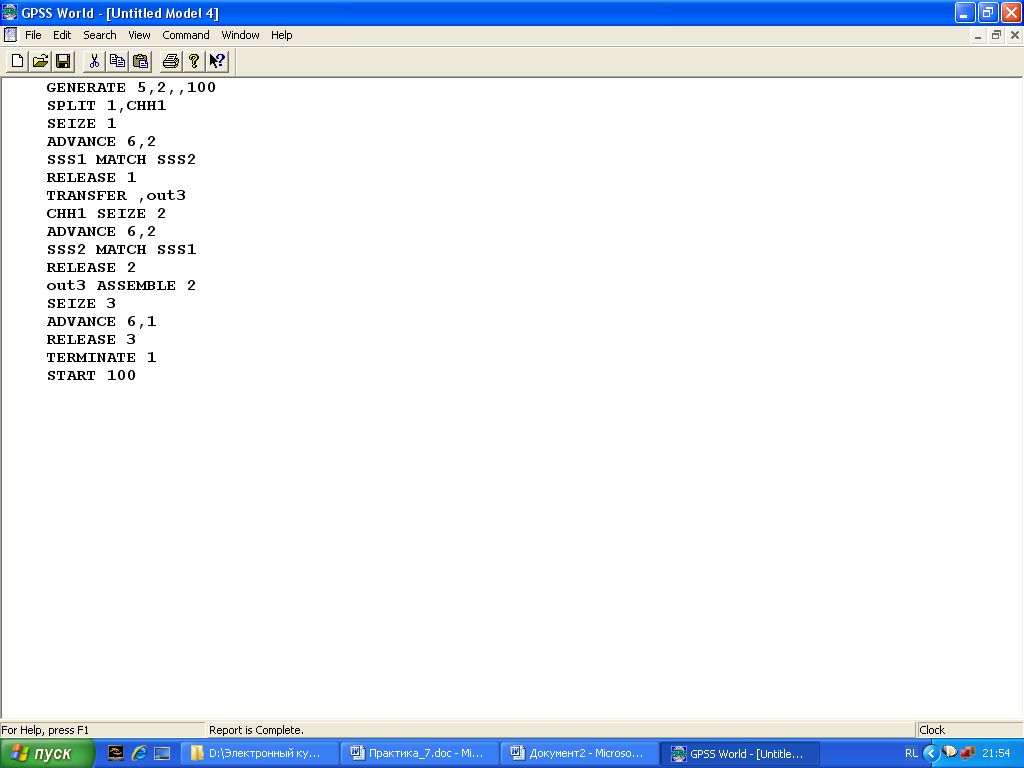
Упражнение  6. На обработку по равномерному закону поступают два потока деталей: 1-ый поток со временем 9-11 мин., 2-ой поток – 23-27 минут. Причем второй поток прерывает изготовление деталей 1-го потока. Время обработки деталей первого потока 4-10 минут, второго потока – 14-16 минут. Смоделировать процесс обработки 100 деталей. 

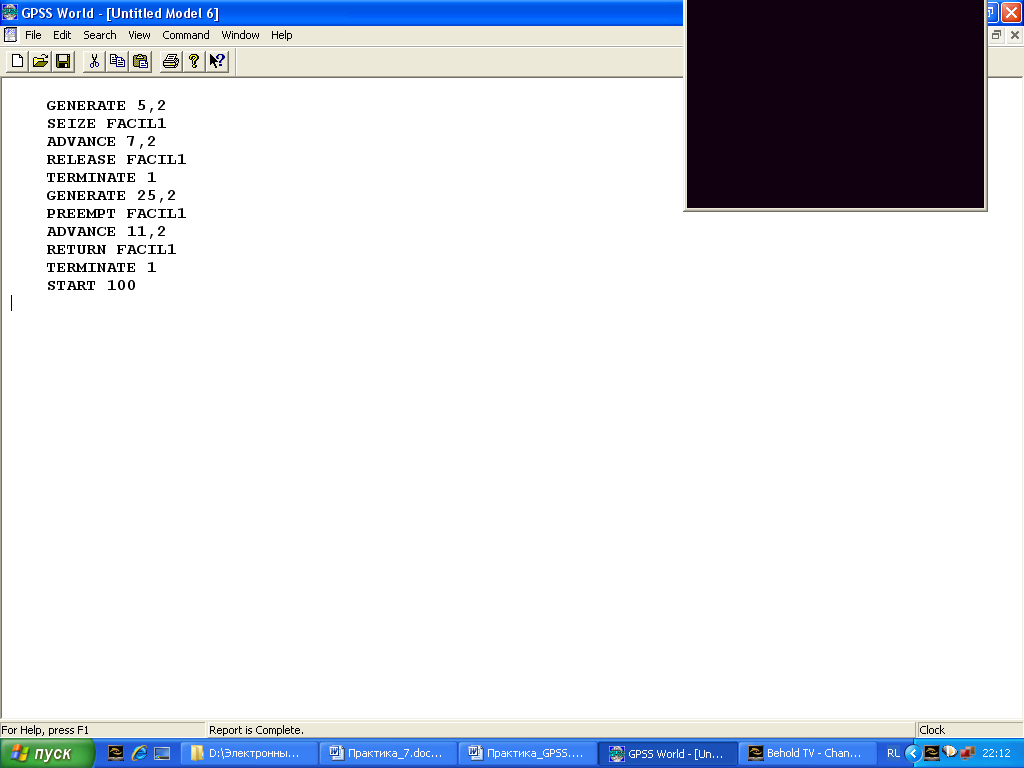
Упражнение 7. Измените условие примера: детали первого потока, обработка которых прервана на время обработки деталей второго потока, выводятся из системы. Промоделируйте обработку 100 деталей. Сравните результаты моделирования системы для случая, когда детали первого потока не выводятся из системы в результате прерывания обработки и когда выводятся. Сделайте выводы.

Содержание отчета и его форма

Отчет к лабораторной работе оформляется в виде текстового документа по форме простого реферата и должен включать:

1. Название лабораторной работы.

2. Цель и содержание лабораторной работы.

3. Краткие выводы по результатам выполнения заданий к лабораторной работе.

4. Формулировку задания для самостоятельной работы и результат его выполнения.

Задания для самостоятельной работы

Базовый уровень

1. Особенности работы с оператором STORAGE .

2. Особенности работы с основными блоками GPSS: ENTER,LEAVE,TRANSFER,TEST, SPLIT,ASSEMBLE,MATCH,PREEMPT,RETURN.  

3. Морские суда прибывают в порт каждые 15-25 часов. В порту имеется 10 причалов. Каждый корабль по длине занимает 3 причала и находится в порту 7-13 часов. Промоделируйте работу порта на протяжении 500 часов. Напишите сегмент GPSS программы. Оцените эффективность работы порта.

4. Выполните следующие задания в среде GPSS с использованием оператора TRANSFER:

4.1. На станцию технического обслуживания, которая состоит из бокса для ремонта и бокса для техосмотра, каждые 15-35 минут поступают автомобили. Из них 73% требуют ремонта, который продолжается 35-55 минут, а 27% проходят техосмотр (9-25 минут). Промоделируйте 40 часов работы станции технического обслуживания.

4.2. Вычислительная система состоит из 3-х компьютеров. С интервалом 3-5 мин в систему поступают задания. Если первый компьютер свободен, то задание поступает на обработку к первому компьютеру (5-7 мин), иначе ко второму (7-11 мин). В случае занятости второго компьютера проверяется, свободен ли третий. Если свободен, то задание обрабатывается с интервалом 8-12 мин. Промоделируйте обработку 100 заданий.

4.3. Измените условие предыдущей задачи: обработка заданий может осуществляться тремя компьютерами равновероятно.

 

Повышенный уровень

5. Выполните следующие задания в среде GPSS с использованием оператора TEST. В программу добавьте условие: если длина очереди BR больше двух, то заявка выводится из системы без обработки. 

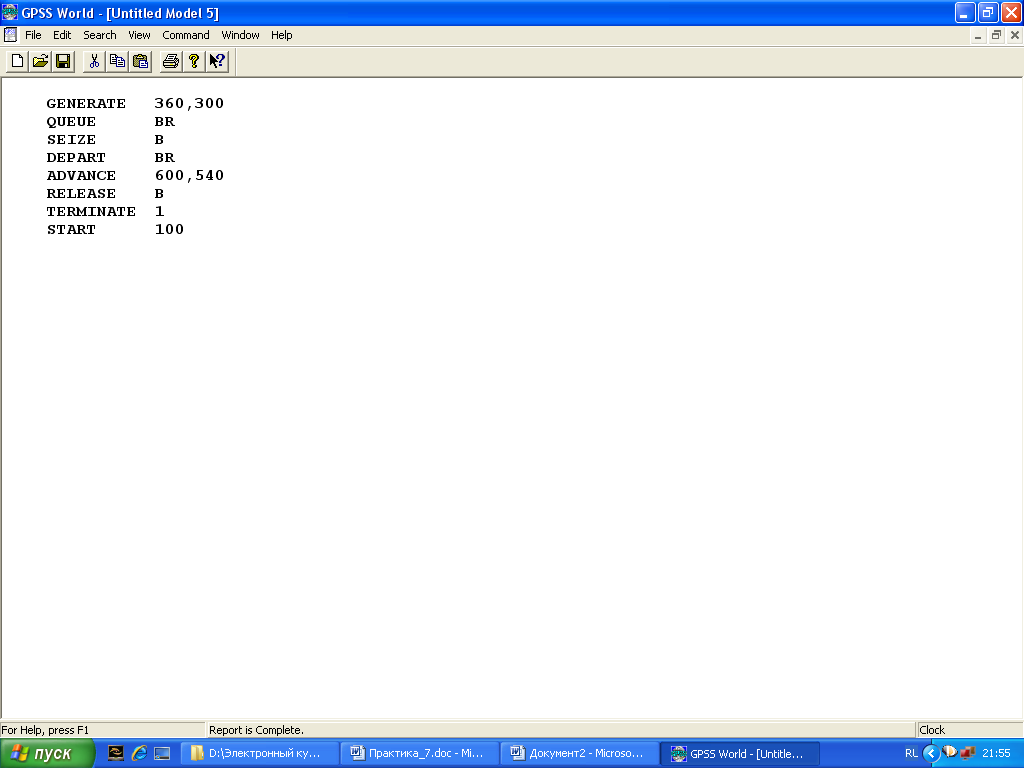
6. Выполните в среде GPSS задание с использованием блоков SPLIT, ASSEMBLE, MATCH.

Некоторая фирма производит центробежные насосы, сборка которых осуществляется по заказу покупателей. Заказы поступают в случайные моменты времени равномерно с интервалом 16-22 мин. Когда поступает заказ, делается две его копии. Оригинал заказа используется для получения двигателя со склада и подготовки его для сборки (время выполнения 6-10 мин.). Первый экземпляр копии используется для заказа и адаптации насоса (время 8-12 мин.), а второй экземпляр для начала изготовления плиты основания (время 15 мин.).

Когда насос и плита основания готовы, производится пробная подгонка (время 4-6 мин.). Далее все три компонента собираются вместе (5-7 мин.). Промоделировать сборку 100 центробежных насосов. Единица модельного времени 1 секунда.

 

Лабораторная работа 13-14

Имя FVARIABLE выражение

Здесь имя - имя переменной, используемое для ссылок на нее, а выражение - арифметическое выражение, определяющее переменную.

Арифметическое выражение представляет собой комбинацию операндов, в качестве которых могут выступать константы, функции, знаки арифметических операций и круглых скобок. Следует заметить, что знаком операции умножения в GPSS является символ #.

Переменные могут быть использованы для получения значений случайной величины с заданным законом распределения. Пусть необходимо сгенерировать 100 значений равномерно распределенной СВ на интервале [5, 15].

TARR FVARIABLE 10#( RN 1/1000)+5

GENERATE V$TARR

TERMINATE 1

START 100

 

Для получения значений случайной величины Y с показательным (экспоненциальным) законом необходимо воспользоваться соотношением , полученным на основе метода обратной функции (см. раздел 7.2. в учебном пособии). Для  имеем:

TERMINATE 1

START 100

Такой способ является достаточно трудоемким, так как требует обращения к математическим функциям, вычисление которых требует десятков машинных операций. Другим возможным способом является использование вычислительных объектов GPSS типа функция.

Функции используются для вычисления величин, заданных табличными зависимостями. Каждая функция определяется перед началом моделирования с помощью оператора определения FUNCTION (функция), имеющего следующий формат:

Имя FUNCTION A , B

Здесь имя - имя функции, используемое для ссылок на нее; A – стандартный числовой атрибут, являющийся аргументом функции; B - тип функции и число точек таблицы, определяющей функцию.

Существует пять типов функций. Непрерывные числовые функции, тип которых кодируется буквой C. Так, например, в определении непрерывной числовой функции, таблица которой содержит 24 точки, поле B должно иметь значение C24.

 При использовании непрерывной функции для генерирования случайных чисел ее аргументом должен быть один из генераторов случайных чисел RNj. Так, оператор для определения функции показательного распределения может иметь следующий вид:

EXP FUNCTION RN 1, C 24

Особенностью использования встроенных генераторов случайных чисел RNj в качестве аргументов функций является то, что их значения в этом контексте интерпретируются как дробные числа от 0 до 0,999999.

Таблица с координатами точек функции располагается в строках, следующих непосредственно за оператором FUNCTION. Эти строки не должны иметь поля нумерации. Каждая точка таблицы задается парой Xi (значение аргумента) и Yi (значение функции), отделяемых друг от друга запятой. Пары координат отделяются друг от друга символом "/" и располагаются на произвольном количестве строк. Последовательность значений аргумента Xi должна быть строго возрастающей.

Как уже отмечалось, при использовании функции в поле B блоков GENERATE и ADVANCE вычисление интервала поступления или времени задержки производится путем умножения операнда A на вычисленное значение функции. Отсюда следует, что функция, используемая для генерирования случайных чисел с показательным (экспоненциальным) распределением , должна описывать зависимость y=-ln(1-x) (данная зависимость получена на основе использования метода обратной функции, см. раздел 7.2. в учебном пособиичена на основе исползсел 1,л.ельность путем изменения начальных мнежителей.

л. ()), представленную в табличном виде.

Оператор FUNCTION с такой таблицей, содержащей 24 точки для обеспечения достаточной точности аппроксимации, имеет следующий вид:

EXP FUNCTION RN 1, C 24

0,0/.1,.104/.2,.222/.3,.355/.4,.509/.5,.69/.6,.915

.7,1.2/.75,1.38/.8,1.6/.84,1.85/.88,2.12/.9,2.3

.92,2.52/.94,2.81/.95,2.99/.96,3.2/.97,3.5/.98,3.9

.99,4.6/.995,5.3/.998,6.2/.999,7/.9998,8

 

Вычисление непрерывной функции производится следующим образом.

Сначала определяется интервал (Xi;Xi+1), на котором находится текущее значение СЧА-аргумента (в нашем примере - сгенерированное значение RN1). Затем на этом интервале выполняется линейная интерполяция с использованием соответствующих значений Yi и Yi+1. Результат интерполяции используется в качестве значения функции. Если функция служит операндом B блоков GENERATE или ADVANCE, то результат умножается на значение операнда A.

Использование функций для получения случайных чисел с заданным распределением дает хотя и менее точный результат за счет погрешностей аппроксимации, но зато с меньшими вычислительными затратами (несколько машинных операций на выполнение линейной интерполяции). По сути, этот вариант реализации (получения последовательности значений СВ) соответствует методу кусочной аппроксимации функции плотности распределения вероятностей.

Функции всех типов имеют единственный системный числовой атрибут с названием FN, значением которого является вычисленное значение функции. Вычисление функции производится при входе транзакта в блок, содержащий ссылку на СЧА FN с именем функции.

При большом количестве транзактов, пропускаемых через модель (десятки и сотни тысяч), разница в скорости вычислений по данному способу и способу, описанному выше, должна стать заметной.

EXP1 FUNCTION RN1,C24

0,0/.1,.104/.2,.222/.3,.355/.4,.509/.5,.69/.6,.915

.7,1.2/.75,1.38/.8,1.6/.84,1.85/.88,2.12/.9,2.3

.92,2.52/.94,2.81/.95,2.99/.96,3.2/.97,3.5/.98,3.9

.99,4.6/.995,5.3/.998,6.2/.999,7/.9998,8

GENERATE 100,FN$EXP1

TERMINATE 1

START 100

Задания к лабораторному занятию

Базовый уровень

Упражнение 1. В примере среднее значение СВ равно 100. Пример табличного задания нормального распределения СВ, используется 25 точки для обеспечения достаточной точности аппроксимации.

NOR 1 FUNCTION RN 1, C 25

0,-5/.00003,-4/.00135,-3/.00621,-2.5/.02275,-2

.06681,-1.5/.11507,-1.2/.15866,-1/.21186,-.8/.27425,-.6

.34458,-.4/.42074,-.2/.5,0/.57926,.2/.65542,.4

.72575,.6/.78814,.8/.84134,1/.88493,1.2/.93319,1.5

.97725,2/.99379,2.5/.99865,3/.99997,4/1,5

Данная таблица задает СВ Z с математическим ожиданием равным 0, и СКО равным 1. Для моделирования нормальной СВ X с другими значениями математического ожидания и СКО необходимо произвести вычисления по формуле:

Если математическое ожидание =5; среднеквадратическое отклонение =2, то

GENERATE (5+2#FN$NOR1)

TERMINATE 1

START 100

 

Повышенный уровень

Упражнение 2. Пример использования блоков TABLE и TABULATE

TT TABLE M1,40,50,8

EXP1 FUNCTION RN1,C24

0,0/.1,.104/.2,.222/.3,.355/.4,.509/.5,.69/.6,.915

.7,1.2/.75,1.38/.8,1.6/.84,1.85/.88,2.12/.9,2.3

.92,2.52/.94,2.81/.95,2.99/.96,3.2/.97,3.5/.98,3.9

.99,4.6/.995,5.3/.998,6.2/.999,7/.9998,8

GENERATE 100,FN$EXP1

ADVANCE 100,FN$EXP1

TABULATE TT

TERMINATE 1

START 100

           

Здесь М1 – константа (стандартный числовой атрибут), которая связана с каждым транзактом и хранит время пребывания транзакта в модели. Время пребывания транзакта в модели определяется блоком ADVANCE и распределено по показательному закону с =1/100. Строится частотное распределение, вычисляются оценки математического ожидания и среднеквадратического отклонения для М1, т.е. для времени пребывания транзакта в модели. Граница первого интервала задана 40; ширина интервала группирования – 50; число интервалов группирования – 8. Все эти параметры задаются опытным путем.

Ниже приведен фрагмент отчета, выдаваемый GPSS по результатам работы программы.

 

Mean – это среднее значение или оценка математического ожидания;

STD . DEV – это оценка среднеквадратического отклонения;

Range – интервалы группирования;

FREQUENCY – количество наблюдений, попавших в каждый интервал.

Таким образом, погрешность в оценке математического ожидания составила:

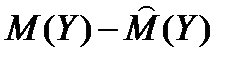= =100-101.032=-1.032

Погрешность в оценке среднеквадратического отклонения составила:

= =100-101.889=-1.889.

Таким образом, точность имитационного моделирования значений СВ по методу кусочной аппроксимации функции плотности распределения вероятностей в среде GPSS достаточно высокая.

Для построения гистограммы необходимо выбрать после выполнения программы пункт меню Window / Simulation Window / Table Window. Далее в открывшемся диалоговом окне задать имя таблицы (в данном примере TT). Вид гистограммы приведен на рис. 1. 

 

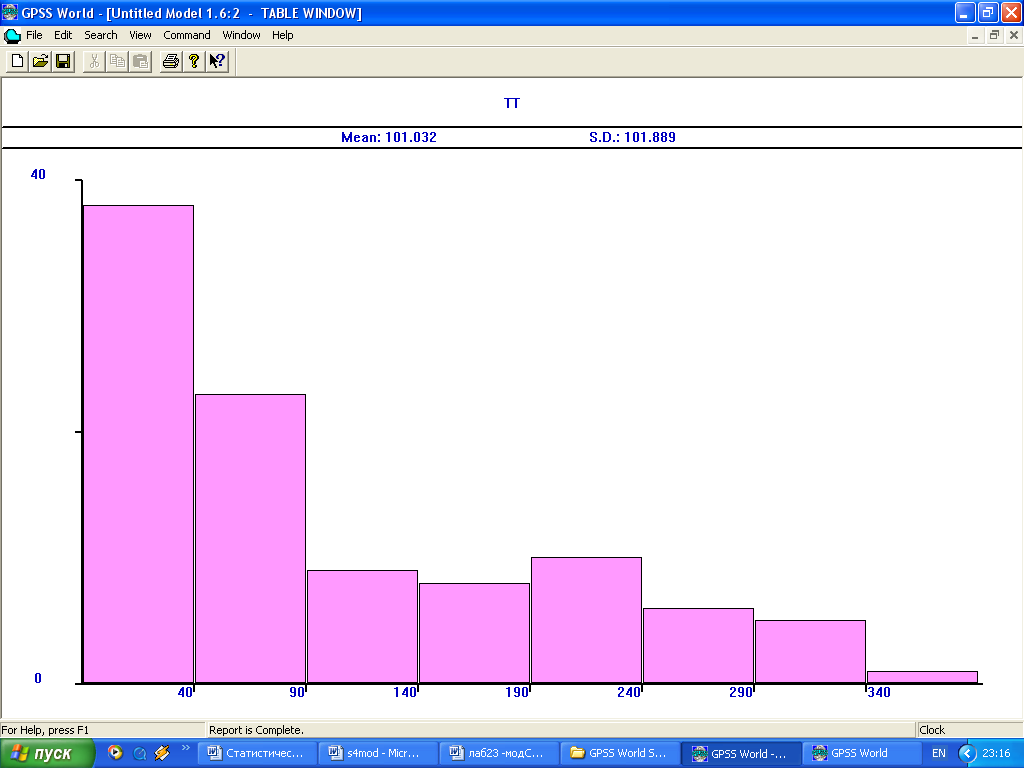
Рисунок 1. Гистограмма значений СВ Y

Визуальный анализ гистограммы позволяет сделать вывод о согласии выборочных значений СВ Y с моделью экспоненциального распределения.

Содержание отчета и его форма

Отчет к лабораторной работе оформляется в виде текстового документа по форме простого реферата и должен включать:

1. Название лабораторной работы.

2. Цель и содержание лабораторной работы.

3. Краткие выводы по результатам выполнения заданий к лабораторной работе.

4. Формулировку задания для самостоятельной работы и результат его выполнения.

Задания для самостоятельной работы

Базовый уровень

1. Особенности работы с операторами: PMULT,FVARIABLE,FUNCTION,TABLE и TABULATE.      

2. Какие существуют оценки точности имитационного моделирования значений СВ.

3. Способ построения гистограммы средствами GPSS.

Повышенный уровень

4. Построить модели согласно заданиям 1 и 2.

 

Лабораторная работа 15-16

В СИСТЕМЕ GPSS WORLD

Теоретическая часть

Этапами разработки имитационного проекта являются:

1.Формулирование и описание проблемы (постановка задачи).

2. Создание концептуальной модели.

Концептуальная модель - это описание в словесной или гра­фической форме элементов оригинала (моделируемой системы), связей между ними (элементами), процессов протекающих в ори­гинале, влияние внешней среды.

При разработке концептуальной модели производится стати­ческое и динамическое описание системы. Определяют границы системы, приводятся описание внешней среды, выделяют сущест­венные элементы и дают их описание, формируют переменные, параметры, функциональные зависимости как для отдельных эле­ментов и процессов, так и для всей системы, ограничения, целе­вые функции (критерии). На данном этапе выдвигаются гипотезы и фиксируют все допущения (предположения), необходимые для построения имитационной модели. Обсуждают уровень детализа­ции моделируемых процессов.

В концептуальное описание системы должны быть включены критерии эффективности функционирования системы и оценивае­мые альтернативные решения, которые рассматриваются как вхо­ды модели. Здесь же уточняются основные переменные модели, участвующие в ее описании.

При создании концептуальной модели производят исключе­ние второстепенных элементов, группировку оставшихся элемен­тов в блоки по функциональному, признаку, окончательно при­нимают предположения и гипотезы о законах распределения пе­ременных (если они заданы).

Основная проблема при этом заключается в нахождении ком­промисса между простотой модели и ее адекватностью исследуе­мой системе. Четко установленных правил концептуального опи­сания модели не существует. Основным требованием на этом эта­пе является четкое и ясное отражение моделируемой системы. Поэтому данный раздел проекта выполняется в произвольной форме. Если моделируемый процесс представляет собой систему массового обслуживания (СМО), то концептуальная модель должна быть описана графически в общепринятых терминах и обозначениях СМО.

Данный пункт включает следующие подпункты:

2.1. Подробная постановка задачи (обоснование целесообраз­ности построения модели, формулировка цели моделирования, описание реальной системы или проблемной ситуации);

2.2. Содержательное описание объекта моделирования (пере­числение основных гипотез, выдвинутых при построении модели).

2.3. Функциональная схема объекта моделирования.

2.4. Список параметров и переменных модели.

2.5. Перечень искомых выходных данных модели (статисти­ка).

2.6.Функциональные зависимости, используемые в концеп­туальном описании.

3. Формирование имитационной модели.

На этом этапе модель, представленная как система массово­го обслуживания, воплощается в конкретную машинную модель, ориентированную на использование конкретных программно-технических средств.

Язык моделирования GPSS имеет блочную концепцию струк­туризации, структура моделируемого процесса изображается в ви­де потока транзактов, проходящего через обслуживающие устрой­ства, очереди и другие элементы систем массового обслуживания.

Удобной формой представления логической структуры ма­шинной модели является схема алгоритма. Она отражает логику функционирования моделируемого объекта и содержит последова­тельность блоков. Общие требования к изображению схем алго­ритмов приведены в ГОСТ 19.003 - 80 «Единая система про­граммной документации» (рис. 1). В системе GPSS World приня­ты свои специальные обозначения (приложение 1).

Рисунок 1. Блок-схема обслуживания на АЗС в соответствии с ГОСТ

 

Кроме того, в некоторых средствах имитационного модели­рования имеется возможность построения логической структуры реальной экономической системы с помощью соответствующих алгоритмических изображений.

4. Подготовка исходной информации.

 

После постановки задачи необходимо сформулировать тре­бования к исходной информации об объекте моделирования. Затем принимают предположения и гипотезы о достаточности информа­ции для решения задачи, об ограничениях на ресурсы при реше­нии задачи, об ожидаемых результатах моделирования.

Кроме этого необходимо определить параметры системы, входные и выходные переменные, факторы воздействия внешней среды.

Описание каждого параметра и переменной дается в следую­щем порядке:

1)  определение и краткая характеристика;

2)  символ обозначения и единица измерения;

3)  диапазон изменения (для переменных);

4)  место применения в модели.

5. Программирование модели.

На данном этапе концептуальное или формальное описание модели сложной системы преобразуется в программу-имитатор в соответствии методикой программирования GPSS (или с помощью других программных средств).

Если схема алгоритма составлена подробно, то написание программы не составит большого труда. Этот шаг заключается в записи пространственной структуры в линейном виде. Если не­обходимо, в программу включаются комментарии, описывающие объекты моделирования: функции, переменные, ячейки и т.п.

6. Анализ и интерпретация результатов пробного прогона модели.

Правильная интерпретация результатов не менее важна, чем анализ исходных данных, так как от этого зависят выводы иссле­дователя по функционированию моделируемой системы. Сначала выделяют те результаты, которые нужны для дальнейшего анали­за. Затем эти результаты должны быть интерпретированы относи­тельно моделируемого объекта, т.е. должен быть осуществлен пе­реход от информации, полученной в результате машинного экспе­римента с моделью, к информации применительно к объекту мо­делирования.

По полученным результатам должна быть проведена провер­ка гипотезы и предположений, сделаны соответствующие выводы и даны рекомендации по практическому использованию результа­тов моделирования. На данном этапе приводятся результаты ком­пьютерных экспериментов в виде графиков, таблиц, распечаток.

7. Исследование свойств имитационной модели.

Полученные с помощью имитационной модели результаты должны обладать требуемой точностью и достоверностью. Досто­верность результатов моделирования предполагает, что имитаци­онная модель отвечает некоторым специфическим требованиям, позволяющим оценить качество модели. Оценка качества модели предполагает ее проверку на соответствие целям моделирования. Оценка свойств модели включает: оценку адекватности модели;

- оценку точности результатов моделирования (погрешности имитации, обусловленную наличием в модели неидеальных генераторов случайных чисел);

- определение длительности переходного режима в работе имитационной модели;

- оценку устойчивости результатов имитации исследуемых процессов; исследование чувствительности модели.

Оценка устойчивости модели

Под устойчивостью результатов имитации понимается сте­пень нечувствительности ее к изменению входных условий. Ус­тойчивость модели - это ее способность сохранять адекватность на всем диапазоне рабочей нагрузки, а также при внесении изменений в конфигурацию системы. Например, при увеличении работы сис­темы с пяти до восьми часов будет ли разработанная модель с дос­таточной точностью отражать работу системы? Чем ближе струк­тура модели соответствует структуре системы и выше степень ее детализации, тем выше устойчивость модели.

В целом устойчивость результатов моделирования можно оценить дисперсией значений отклика (одного из показателей ра­боты системы, например, коэффициента загрузки устройства). Если при увеличении времени моделирования дисперсия отклика не увеличивается, то результаты работы данной модели устойчивы.

Для получения первой выборочной статистической совокуп­ности, устанавливается какое-либо модельное время, например, пять часов. Затем выбирается некий шаг для контроля величины параметра работы системы, допустим, каждые 30 мин. Выбороч­ная совокупность будет состоять из десяти значений. Проводится расчет дисперсии (D₁). Затем модельное время увеличивается, на­пример, с пяти до восьми часов, и снова осуществляется прогон модели. Новая выборочная совокупность содержит уже 16 значе­ний. Рассчитывается новая дисперсия (D₂). Затем все рассчитан­ные дисперсии сравниваются между собой.

Чтобы результаты моделирования были устойчивыми, дис­персии должны различаться несущественно. Рост разброса кон­тролируемого параметра от начального значения при изменении числа шагов указывает на неустойчивый характер имитации ис­следуемого процесса. Четко установленной методики для проце­дуры проверки устойчивости модели не существует.

Можно установить границы колебания контролируемого па­раметра экспертным путем и если данный параметр выходит за пределы колебаний, то на данном временном интервале констати­руется потеря устойчивости результатов моделирования.

Реже для проверки существенности различия дисперсий ис­пользуется критерий Бартлетта, расчетное значение которого оп­ределяется по формуле:

где

Методика проверки статистической гипотезы следующая:

1) Выдвигается нулевая гипотеза Н₀ о несущественности, расхождений дисперсий значений откликов.

2) По вышеуказанной формуле рассчитывается фактическое значение критерия Бартлетта (B_факт).

3) Определяется теоретическое (табличное) значение крите­рия Бартлетта (B_табл).

4) Сравниваются B_факт и B_табл. Если фактическое значение превышает табличное, то гипотеза о несущественности расхожде­ний дисперсий значений откликов отвергается и принимается про­тивоположная гипотеза (т.е. характер имитации неустойчив), если наоборот - нулевая гипотеза принимается.

Для оценки устойчивости модели может быть также исполь­зован статистический критерий Вилкоксона.

Планирование и проведение имитационного эксперимента

Перед проведением рабочих расчетов на ЭВМ должен быть составлен план проведения эксперимента с моделью. При этом нужно четко представлять, какие параметры системы исследуются (зависимые), а какие параметры при этом нужно задавать (незави­симые). Далее определяется количество прогонов, необходимых для исследования системы. Затем определяется способ получения результатов и их обработки. Чаще всего для получения результа­тов достаточно стандартной статистики.

После составления плана проведения эксперимента, можно приступить к выполнению рабочих расчетов и получению резуль­татов моделирования. Моделирование рационально выполнять в два этапа: сначала контрольные, а затем рабочие расчеты. Кон­трольные расчеты проводятся для проверки машинной модели и определения чувствительности результатов к изменению исходных данных.

Оптимизирующий эксперимент

Иногда постановка имитационной задачи предполагает нахо­ждение оптимального значения какого-либо параметра системы или сочетания набора ее элементов. Для характеристики этих экс­периментов будем оперировать следующими общепринятыми терминами и понятиями.

Факторы - это входные переменные (или входы), от которых зависят результирующие показатели работы моделируемой систе­мы. Отклик (выход) - это выходные переменные модели, они являются зависимыми. Как правило, факторы (или факторные при­знаки) обозначают х, а отклики - у. Например, в системе «сельско­хозяйственное предприятие» факторами являются такие характе­ристики как количество вносимых удобрений, соотношение средств производства и рабочей силы, количество солнечной ра­диации и др. Откликами являются такие характеристики работы системы как выход валовой продукции, прибыль, рентабельность и др.

Уровнями фактора называют различные значения, которые данный фактор может принимать. Понятно, что между уровнями фактора и откликами существует некая связь, отражающаяся функцией отклика:

где y_l - l-й отклик;

п - число анализируемых откликов;

х _i - i-й фактор;

т - число факторов.

Если функцию отклика представить в виде некой многомер­ной области, то она будет называться поверхностью отклика. Функция отклика формируется после проведения серии экспери­ментов с моделью и представляет собой уравнение регрессии, по­лученное методом наименьших квадратов.

На отклики системы может влиять множество факторов, ко­торые также взаимодействуют между собой. Из множества факто­ров можно выделить наиболее существенные, используя процеду­ру отсеивающего эксперимента. Далее, если поставлена такая цель, находят экстремальные значения на поверхности отклика пу­тем подъема по поверхности отклика к вершине. При этом обычно используют метод скорейшего подъема - процедура пошагового подъема. Направление скорейшего подъема показывает относи­тельные величины изменения факторов, обеспечивающих макси­мальное увеличение отклика. Поверхность отклика может иметь несколько максимумов.

Функция отклика обычно представляется в виде полинома первого порядка, реже - второго или третьего. Если это - полином первого порядка, то функция выглядит следующим образом:

у=а₀ + а₁x₁ + а₂x₂ +...+ а _kх_к.

Для характеристики этих экспериментов будем оперировать следующими общепринятыми терминами и понятиями.

В этом случае используют встроенную в GPSS Word проце­дуру оптимизирующего эксперимента. Данный эксперимент предназначен для построения уравнения регрессии (поверхности отклика) для заданных факторов и поиска оптимального значения вычисляемого в модели значения (максимального или минималь­ного).

Задания к лабораторному занятию

Базовый уровень

Подготовка исходной информации

Представленная система относится к системам массового обслуживания с 2-мя обслуживающими устройствами. Это - ра­зомкнутая система массового обслуживания.

Динамическими элементами системы являются - автомоби­ли.

Обслуживающие устройства - колонки АЗС (табл. 1).

Таблица 1 - Определение основных входных данных

Элемент систе­мы	Роль в системе	Обозначение
Автомобиль	Транзакт	-
Колонки: №1             №2	Устройства обслуживания	KOLONKAJ, KOLONKAJ.
Очередь	-	ZAPRAVKA

Программирование модели

После того, как программа написана, ее нужно отладить и проверить с помощью тестовых задач. В окне Journal выдаются сообщения об ошибках.

Повышенный уровень

Содержание отчета и его форма

Отчет к лабораторной работе оформляется в виде текстового документа по форме простого реферата и должен включать:

1. Название лабораторной работы.

2. Цель и содержание лабораторной работы.

3. Краткие выводы по результатам выполнения заданий к лабораторной работе.

4. Формулировку задания для самостоятельной работы и результат его выполнения.

Задания для самостоятельной работы

Базовый уровень

1. Охарактеризуйте каждый из этапов разработки имитационного проекта.

2. С какой целью используют при исследовании свойств имитационной модели критерий t-Стьюдента?

3. Для чего проводят несколько прогонов модели при оценке результатов моделирования?

4. Какие критерии используют для оценки устойчивости модели?

5. Охарактеризуйте назначение процедуры «отсеивающий эксперимент».

6. Что определяет дисперсионный анализ?

7. Охарактеризуйте назначение процедуры «оптимизирующего эксперимента».

Повышенный уровень

8. В сельскохозяйственной организации работает ремонтный цех. На текущий ремонт поступают грузовые автомобили и трактора. Интервал их поступления и время обслуживания представлены в таблице:

Вид техники	Интервал поступления, мин	Время обслуживания, мин
Грузовые автомобили	55 ±15	28 ±5
Трактора	35 ±10	30 ±8

 

Какова себестомость произведенной работы за время моделирования, если себестоимость ремонта автомобиля - 1 500 р., а трактора - 2 000 р.

На текущий ремонт также поступает транспорт главных специалистов хозяйства, который обслуживается вне очереди. Интервал поступления составляет 180 ± 20минут, время обслуживания 30 ± 5 мин. Необходимо смоделировать работу участка в течение 40 ч. Определить длину очереди на текущий ремонт и среднее время ожидания обслуживания. Внести предложения по сокращению времени обслуживания в системе.

Оценить статистически, существенно ли уменьшится длина очереди грузовых автомобилей, если время их обслуживания сократится с 28 до 20 мин.

9. В информационном центре производят обра­ботку заказов на реализацию. Принимаются три класса заказов: розничные, мелкооптовые и крупнооптовые. Розничные заказы поступают через 20 + 5 мин, мелкооптовые - через 20 ± 10 мин и крупнооптовые заказы - через 50 ± 10 мин. Продолжительность оформления: розничные заказы - 20 ± 5 мин, мелкооптовые - 21 ± 3 мин и крупнооптовые - 28 + 5 мин.

Исходя из наличия функциональных возможностей ЭВМ, заказы по рознице и мелкому опту принимаются и обрабатываются одновременно, а крупнооптовые заказы выполняются вне очереди. Смоделировать работу информационного центра за 80 ч. Оп­ределить загрузку Центра.

Если крупнооптовые заказы будут комплектовать два работ­ника, и затрачивать на это не 28, а 25 мин, то, существенно ли это сократит длину очереди (оценить статистически).

10. На ремонтный участок МТС, который состоит из 2-х боксов (для ремонта и для техосмотра) через каждые 20 ± 3 минуты поступают тракторы. Из них 60 % требуют ремонта, кото­рый продолжается 40 ± 15 минут, 40 % тракторов проходят техни­ческий осмотр продолжительностью 20 + 5 мин. Смоделировать работу участка в течение 100 ч. Опре­делить вероятность отказа в обслуживании. Рассмотреть основные характеристики работы системы. Предложить меры по оптимиза­ции обслуживания техники, используя инструмент ANOVA.

Какова общая стоимость выполненной работы, если стои­мость ремонта составляет 200 р., а техосмотра - 50 р.

11. На участке происходит сортировка и упаковка яб­лок, которые поступают в ящиках через 20 ± 5 мин. Сортировка одного ящика занимает 10 ± 7 мин, а упаковка - 7 ± 5 мин. Сорти­ровкой занимается один работник, а упаковкой - другой. Известно среднее время для передачи яблок от одного работника к другому - 2 ± 1мин.

Смоделировать процесс работы участка в течение 8 ч. Определить длину очереди на этапе сортировки и упаковки.

Внести предложения по сокращению длины очереди, т.е. насколько должно уменьшиться время обслуживания, чтобы это значительно сократило очередь (провести несколько экспериментов ANOVA)?

Какова дневная зарплата работников, если за один отсортированный ящик рабочие получают 30 р.

12. На складе ремонтного предприятия работают 2 кладовщика. Один из кладовщиков (первый) выполняет работу по поиску и выдаче запасных частей немного быстрее. Поэтому ра­ботники отдают предпочтение первому кладовщику. Работники предприятия заходят на склад для поиска и получения запасных частей каждые 7 ± 2 минуты. Первый кладовщик обслуживает ра­ботника за 3 ± 1 минуты, второй за 5 ± 1 минуты. Промоделируйте работу склада на протяжении 40 ч. Определите длину очереди и время ожидания обслуживания к каждому кладовщику. Насколько существенной для результатов будет замена второго кладовщика на работающего более быстро и выполняющего заказ не за 5, а за 4 мин? Оценить статистически.

13. Диспетчер управляет внутризаводским транспор­том и имеет в своем распоряжении два грузовика. Заявки на пере­возки поступают к диспетчеру каждые 5 ± 4 мин. Диспетчер запрашивает по радио один из грузовиков и передает ему заявку, ес­ли тот свободен. В противном случае он запрашивает другой гру­зовик и таким образом продолжает сеансы связи, пока один из грузовиков не освободится. Диспетчер допускает накопление у се­бя до пяти заявок, после чего вновь прибывшие заявки получают отказ. Грузовики выполняют заявки на перевозку за 12 ± 8 мин.

Смоделировать работу внутризаводского транспорта в тече­ние 10 ч. Подсчитать число обслуженных и отклоненных заявок. Определить коэффициенты загрузки грузовиков.

Оценить статистически целесообразность замены грузовиков на более производительные, выполняющие перевозку за 8 мин.

14. В ремонтную мастерскую тракторов ООО «Са­лют» на капитальный ремонт поступают тракторы каждые 50 ± 10 дней, ремонт длится 20 ± 5 дней. Текущий ремонт (замена и ре­монт топливного насоса, замена свечей, колес и т.д.) производится за 1,5 ± 0,5 дня. Необходимость в текущем ремонте возникает в среднем каждые 10 ± 3 дня. В мастерскую поступают также ма­шины работников аппарата управления хозяйством через 15 ± 5 дней, которые имеют более высокий приоритет обслуживания, чем капитальный ремонт, но ниже, чем текущий. Их ремонт про­изводится обычно за 5 + 1 день. Необходимо:

1)  Смоделировать работу мастерской в течение полугода.

2)  Определить коэффициент использования мастерской. Мастерская функционирует по принципу хозрасчета. Если капитальный ремонт трактора дает чистый доход в размере 5 000 р., а текущий - 3 000 р., то каков будет чистый доход от проведения ремонта за период моделирования?

Если покупка нового оборудования для ремонта увеличит скорость текущего ремонта тракторов с 1,5 до 0,7 дня, существен­но ли это отразится на уменьшении очереди? Оценить статистиче­ски.

15. В картофелехранилище процесс сортировки кар­тофеля организован следующим образом: через 10 ± 5мин на сор­тировочный пункт, где работает два сортировщика, поступает два мешка картофеля на переборку. В целях ведения индивидуального учета выполненной работы каждый работник перебирает отдель­ный мешок. Первый работник сортирует содержимое одного меш­ка за 15 ± 3 мин, второй - за 18 ± 5 мин. Если первый работник за­нят переборкой во время поступления очередной партии мешков, то мешки поступают ко второму работнику (если он уже освобо­дился).

Определить коэффициент использования первого и второго работника и число отсортированных ими мешков картофеля.

Если выручка от реализации одного мешка картофеля (50 кг) составляет 3500 р., а себестоимость производства и реализации 1 кг картофеля (включая сортировку), составляет 4 р., то какова прибыль предприятия от реализации картофеля за данный день (рассчитать по данным стандартного отчета).

Если второго рабочего заменить на рабочего, выполняющего эту работу за 8 минут, существенно ли это повлияет на общую скорость их работы и уменьшит ли число мешков, принесенных в хранилище и требующих переборки? Оценить статистически.

16. В пекарню, где работает два работника, через 20 ± 5 минут поступает партия (мешок) муки. Если в момент поступ­ления мешка первый работник, изготавливающий кондитерские изделия за 40 ± 7 мин, занят, то мешок берет второй работник, пе­рерабатывающий его за 30 ± 5 мин. Промоделировать работу цеха в течение 8 ч.

Определить коэффициент использования первого и второго работника и число использованных ими упаковок с мукой.

Если выручка от реализации кондитерских изделий, произве­денных из одной упаковки, составляет 200 р., а себестоимость их производства и реализации составляет 150 р., то какова прибыль предприятия от реализации кондитерских изделий за данный день (рассчитать по данным стандартного отчета).

Если первого работника обязать работать быстрее и выпол­нять эту операцию за 32 ± 5 минут, существенно ли это повлияет на общую скорость их работы и существенно ли уменьшит оче­редь? Оценить статистически.

17. Частота поломок компьютеров сети подчиняется пуассоновскому потоку интенсивностью l = 0 и b = 20. Сломав­шийся компьютер немедленно ремонтируется. Время ремонта компьютера составляет 30 ± 10 мин. Промоделировать работу сис­темы в течение 8-и часового рабочего дня.

Получить стандартный отчет о результатах моделирования.

Определить:

а) коэффициент использования компьютеров;

б)среднее время ремонта компьютера;

в) количество обращений к мастеру в течение смены.

Если нанять мастера по ремонту компьютеров, ремонтирую­щего один компьютер за 20 мин, а не за 30 мин, как предыдущий, существенно ли это отразится на результатах работы системы? Оценить статистически.

Если ремонт одного компьютера обходится 200 р., то какова стоимость произведенного за смену ремонта?

18. В ремонтной мастерской изготавливают гайки диаметром 10 и 12 мм, используя при этом три разных станка. Ин­тервалы поступления в мастерскую заготовок для изготовления га­ек первого вида составляют 50 ± 7 мин, а заготовок для гаек второго вида - 25 ± 4 мин. Время обработки этих заготовок следующее:

Вид работы	Гайки 1-го вида	Гайки 2-го вида
Резка	16±4	18 ±3
Нарезка резьбы	25 ±5	27 ±5
Упаковка	20 ±3	21 ±4

 

Смоделировать работу мастерской за 8-часовои рабочий день при двусменном режиме.

Определить:

1)  среднюю загрузку каждого станка;

2)  среднее время изготовления детали каждого вида;

3)  длину очереди перед каждым станком;

4) объем упаковочной тары для каждого вида гаек (шт.).

Если чистый доход от реализации гайки первого вида составляет 0,8 р., а второго вида - 1,2 р., то каков чистый доход за год при работе в данном режиме.

Каково будет управленческое решение по возможной замене машины, производящей упаковку гаек второго вида, что увеличит скорость упаковки с 21 мин до 18 мин (используя статистические критерии).

19. В плодоовощном цехе производится мойка яблок и груш и их упаковка в пластиковые контейнеры для последующей реализации. При этом используются моечная и упаковочная ма­шины. Интервалы поступления в цех ящиков с яблоками составля­ет 10 ± 5 мин, а ящиков с грушами - 15 ± 4 мин. Время мойки и упаковка яблок и груш составляет:

Вид работы	Яблоки			Груши
Мойка	10±1			12 ±3
Упаковка		5±2	7±3

 

Смоделировать работу цеха за 8-часовой рабочий день.

Определить:

1)  среднее время мойки и упаковки фруктов каждого вида;

2)  среднюю загрузку моечной и упаковочной машин;

3)  длину очереди перед каждой машиной;

4)  объем тары для перевозки каждого вида фруктов (ящи­ков).

Если прибыль от реализации одного контейнера с яблоками составляет 30р., а от реализации груш - 50 р., то какова дневная прибыль предприятия?

Каково будет управленческое решение по возможной замене машины, производящей мойку груш, что увеличит скорость мойки с 12 до 7 мин (использовать статистические критерии).

20. В период заготовки овощей на овощную базу хо­зяйства поступают грузовые автомобили с овощами, которые про­ходят процедуру взвешивания. В связи с напряженным графиком работы на базе открыто две весовые. Поток автомобилей, посту­пающих на эти весовые, подчиняется экспоненциальному закону распределения вероятностей с параметрами l = 0 и b = 7,1. Время взвешивания на первых весах составляет 8 ± 3 мин, на вторых ве­сах - 10 ± 4 мин. Машина подъезжает к свободным весам.

Смоделируйте работу весовой в течение рабочей смены (8 ч).

Определить:

1)  коэффициент загрузки каждых из весов;

2)  среднее время взвешивания на первых и вторых весах;

3) максимальное, среднее и текущее число автомобилей в очереди к весам;

4) среднее время нахождения автомобиля в очереди.

Подсчитано, что условный убыток от простоя одного автомо­биля в течение 1 мин составляет 5 р., то каков условный убыток от простоя автомобилей в очереди к весам за одну смену?

Если заменить вторые весы на более производительные, взвешивающие за 7 минут, то существенно ли это повлияет на среднее время нахождения автомобилей в каждой очереди (оце­нить статистически).

21. На молочный завод из хозяйств приезжают мо­локовозы, сдающие молоко на анализ в лабораторию завода. На заводе имеется две лаборатории. Поток молоковозов, поступающих на завод, подчиняется экспоненциальному закону распреде­ления вероятностей с параметрами l = 0 и b = 6,8. Время анализа молока в первой лаборатории, имеющей специальное оборудова­ние, составляет 15 ± 3 мин, во второй лаборатории - 20 ± 4 мин. Машина подъезжает к освободившейся лаборатории.

Смоделируйте работу по анализу молока в течение рабочей смены (8 ч).

Определить:

1)  среднее время нахождения молоковоза в очереди;

2)  среднее время анализа в первой и второй лабораториях;

3) максимальное, среднее и текущее число молоковозов в очереди;

4) коэффициент загрузки каждых весов.

Если во второй лаборатории установить оборудование, кото­рое будет производить анализ за 15 мин, то существенно ли это уменьшит длину очереди (эксперимент ANOVA)?

Подсчитано, что условный убыток от простоя одного моло­ковоза в течение 1 мин составляет 7 р. Каков условный убыток в хозяйстве от простоя молоковоза в очереди к лабораториям за од­ну смену?

22. В банк приходят клиенты для оформления опла­ты за коммунальные услуги. В расчетном зале работает два опера­тора по оформлению данных операций. Поток посетителей банка подчиняется равномерному закону распределения с интенсивно­стью 3 ± 1 мин. Первый оператор производит расчет быстрее - за 8 ± 2 мин., второй - за 10 ± 3 мин. Клиент подходит к свободному оператору.

Смоделируйте работу банка в течение рабочей смены (8 ч).

Определить:

1)  коэффициент загрузки каждого из операторов;

2)  среднее время обслуживания клиентов первым и вторым операторами;

3)  максимальное, среднее и текущее число клиентов в очере­ди;

4)  среднее время нахождения клиента в очереди.

Если за обслуживание одного клиента банк берет комиссион­ные 10 р., то какова сумма комиссионных, полученных банком за день?

 

 

СПИСОК ЛИТЕРАТУРЫ

Основная

1. Лычкина Н. Н. Имитационное моделирование экономических процессов: Учебное пособие / Н.Н. Лычкина. – М.: ИНФРА-М, 2014. – 254 с. http://znanium.com/catalog.php?bookinfo=429005

2. Сосновиков Г. К. Компьютерное моделирование. Практикум по имитационному моделированию в среде GPSS World: Уч. пос. / Г.К. Сосновиков, Л.А. Воробейчиков. – М.: Форум: НИЦ ИНФРА-М, 2015. – 112 с. http://znanium.com/catalog.php?bookinfo=500951

Дополнительная

3. Кобелев Н. Б. Имитационное моделирование: Учебное пособие / Н.Б. Кобелев, В.А. Половников, В.В. Девятков; Под общ. ред. д-ра экон. наук Н.Б. Кобелева. – М.: КУРС: НИЦ Инфра-М, 2013. – 368 с. http://znanium.com/catalog.php?bookinfo=361397

4. Каталевский Д. Ю. Основы имитационного моделирования и системного анализа в управлении: Учебное пособие / Каталевский Д.Ю., - 2-е изд., перераб. и доп. – М.:Дело, 2015. – 496 с. http://znanium.com/catalog.php?bookinfo=560665

 

ПРИЛОЖЕНИЕ 1

СОДЕРЖАНИЕ

 

ВВЕДЕНИЕ.. 4

Лабораторная работа 1-2. 6

ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ ИНВЕСТИЦИОННЫХ РИСКОВ.. 6

Лабораторная работа 3-4. 25

ИМИТАЦИЯ В MS EXCEL С ИСПОЛЬЗОВАНИЕМ ИНСТРУМЕНТА.. 25

"ГЕНЕРАТОР СЛУЧАЙНЫХ ЧИСЕЛ". 25

Лабораторная работа 5. 35

СТАТИСТИЧЕСКИЙ АНАЛИЗ РЕЗУЛЬТАТОВ ИМИТАЦИИ.. 35

Лабораторная работа 6-7. 42

ВВЕДЕНИЕ В СИСТЕМУ МОДЕЛИРОВАНИЯ VENSIM 5.0 PLE.. 42

Лабораторная работа 8. 58

МОДЕЛИРОВАНИЕ СИСТЕМ СРЕДСТВАМИ GPSS WORLD.. 58

Лабораторная работа 9-10. 79

МОДЕЛИРОВАНИЕ ОДНОКАНАЛЬНЫХ УСТРОЙСТВ.. 79

Лабораторная работа 11-12. 88

МОДЕЛИРОВАНИЕ МНОГОКАНАЛЬНЫХ УСТРОЙСТВ.. 88

Лабораторная работа 13-14. 105

МОДЕЛИРОВАНИЕ ЗНАЧЕНИЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ С ЗАДАННЫМ... 105

ЗАКОНОМ РАСПРЕДЕЛЕНИЯ И ОБРАБОТКА РЕЗУЛЬТАТОВ.. 105

МОДЕЛИРОВАНИЯ СРЕДСТВАМИ GPSS WORLD.. 105

Лабораторная работа 15-16. 113

РАЗРАБОТКА ИМИТАЦИОННОГО ПРОЕКТА.. 113

В СИСТЕМЕ GPSS WORLD.. 113

СПИСОК ЛИТЕРАТУРЫ... 150

 

 

ВВЕДЕНИЕ

 

 

Рыночная экономика с быстро меняющейся конъюнктурой требует от специалистов любого звена экономики своевременного принятия адекватных управленческих решений. Информатизация всех сфер национальной экономики, обусловила необходимость разработки электронного курса по имитационному моделированию экономических процессов, позволяющему вырабатывать такие решения с использованием компьютерной техники и технологии.

Методические указания посвящены овладению умениями и навыками использования компьютерных средств и информационных технологий для эффективного решения основных задач организации управленческой и экономической деятельности.

Методические указания предназначены для студентов, изучающих дисциплину «Имитационное моделирование экономических процессов».

Целью изучения дисциплины «Имитационное моделирование экономических процессов» является формирование системного представления об имитационном моделировании экономических процессов.

Задачами дисциплины являются:

‒ рассмотрение современных концепций построения моделирующих систем,

‒ всестороннее освещение подходов и способов применения имитационного моделирования в проектной экономической деятельности и новых инструментальных средств этой области. 

В результате изучения дисциплины каждый студент должен

иметь представление:

‒ о перспективах развития систем имитационного моделирования;

‒ о направлениях в области имитационного моделирования экономических процессов, различных подходах к построению имитационных моделей;

‒ о возможностях, преимуществах и недостатках различных сис­тем моделирования, используемых при решении различных экономических задач.

знать:

‒ основные определения и базовые понятия, касающиеся теоретических основ имитационного моделирования, метод Монте-Карло;

‒ технологию создания, отладки и эксплуатацию моделей экономических систем с использованием CASE- технологий конструирования моделей «без программирования» - с помощью диалогового графического конструктора;

‒ модели основных систем массового обслуживания;

‒ состояние и тенденции развития программного обеспечения;

‒ технологический процесс подготовки и решения задач на ПЭВМ.

уметь:

‒ разрабатывать алгоритмы для имитационного моделирования экономических задач;

‒ решать конкретные задачи по разработке имитационных моделей экономических систем;

‒ оформлять программную документацию;

‒ моделировать процессы массового обслуживания в экономических системах;

‒ рассчитывать показатели эффективности операций в экономических системах при их имитационном моделировании;

‒ осуществлять анализ результатов имитационного моделирования экономических процессов.

Компетенции обучающегося, формируемые в результате освоения дисциплины

б) профессиональные компетенции (ПК):

- – способностью осуществлять и обосновывать выбор проектных решений по видам обеспечения информационных систем (ВПК-20) (лабораторные работы№№1-16).

- способностью проводить оценку экономических затрат и рисков при создании информационных систем (ВПК-21) (лабораторные работы№№1-2, 5).

 

Лабораторная работа 1-2

12345678910Следующая ⇒

Поделиться: