
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Классификация трубопроводовСтр 1 из 10Следующая ⇒
Введение В конспекте изложены три темы, обязательные в общем курсе гидравлики. Первая посвящена расчету трубопроводов – основных элементов всех гидравлических сетей и систем и поэтому является важнейшей в смысле практических применений. В последующих двух темах рассматриваются задачи, связанные с истечением жидкостей из отверстий, а также задачи гидродинамического моделирования. Ввиду больших трудностей при изучении течений жидкостей моделирование часто является основным методом исследования. По этой причине подробно рассмотрены многие критерии подобия и связанные с ними примеры решения задач. Для закрепления теоретического материала приведено значительное число задач, решение которых обязательно. Как и в остальных частях конспекта лекций, изложение ведется на двух уровнях: основная часть изложена на первом – низшем уровне. Усвоив этот основной объем, студент может рассчитывать на минимальную положительную оценку на экзамене. Окончательное деление всего материала на части, соответствующие оценкам, может провести преподаватель. Гидравлические расчеты трубопроводов Классификация трубопроводов Трубопроводы нашли исключительно широкое применение в водоснабжении, транспортировке нефти и газа, в системах теплоснабжения, в различных энергетических и двигательных установках. Жидкость движется по трубопроводу вследствие того, что ее потенциальная энергия в начале трубопровода больше, чем в конце. Эта разность потенциальных энергий необходима для преодоления гидравлических сопротивлений между рассматриваемыми сечениями трубопровода. Она может быть создана разными способами: а) работой насоса; б) благодаря разности уровней жидкости – самотечная подача; в) из-за повышенного давления газа на свободную поверхность жидкости в баке – вытеснительная подача. При расчете трубопроводов используются: уравнение неразрывности, уравнение Бернулли, зависимости для расчета сопротивлений и экспериментальные данные. Простыми трубопроводами называют такие, у которых диаметр трубы, а также расход жидкости на всем протяжении остаются неизменными, а сложными – все остальные. Любой сложный трубопровод всегда возможно представить состоящим из ряда простых. Параллельное соединение При параллельном соединении участков трубопровода жидкость, подходя с расходом Q к точке их разветвления А, распределяется по ответвлениям и далее снова собирается в точке их соединения В, рис. 4.2. При параллельном соединение обычно заданы o Суммарный расход до точки разветвления, o Длина, диаметр, величина кэ каждой ветви. Основными задачами гидравлического расчета в этом случае являются. o Определение расходов Q 1, Q 2, Q 3, …, Qn, на отдельных участках, соединенным параллельно. o Определение потерь напора Δ h между точками А и В, на каждом участке. При решении задачи прежде всего учтём очевидное условие: равенство расхода Q сумме всех расходов на отдельных участках
Δ h = Δ h 1 = Δ h 2 = Δ h 3 = …= Δ h n Решая систему уравнений (4.5), можно выразить все расходы через один (например, через Q1) и подставив затем эти значения расходов в (4.4) найти Q1. после этого с помощью (4.5) определяют последовательно расходы Q2, Q3, …, Qn, а по любому из уравнений системы (4.5) определяют потери напора Н. Задача 4.2. Определить расходы и потери напора в каждой из n параллельно соединенных ветвей, считая, что как местные сопротивления, так и сопротивления по длине – в квадратичной области. Решение: В общем случае имеем для потерь в каждой ветви

Имеем также
Примем обозначения
тогда уравнения (4.6) перейдут в такие

Из последнего уравнения выражаем все расходы через один, например через Q1

Затем из (4.7) получаем
Решая последнее уравнение относительно Q1, определим его значение, а из (4.9) и все остальные расходы; по любой из зависимостей (4.6) находим hW. Задача 4.3. Определить расходы и потери в каждой из трех ветвей параллельной сети, если длины и диаметры каждой из них равны соответственно l1, l2, l3 и d1, d2, d3. Известно, что местных сопротивлений нет, расход перед точкой разветвления равен Q, кинематический коэффициент вязкости n и то, что во всех трех ветвях движение ламинарное. Открытые каналы Безнапорное движение жидкости имеет место в открытых руслах и характерно тем, что на свободной поверхности жидкости давление равно атмосферному, например, реки, каналы, лотки и т.д. При равномерном движении гидравлические элементы потока – площадь сечения, глубина и т.д. не изменяются по его длине; следовательно, равномерное движение невозможно в естественных руслах. На рис. 6.1 показан профиль потока в условиях равномерного движения. Глубина вдоль течения постоянна, поэтому гидравлический уклон равен пьезометрическому, т.е. уклону свободной поверхности и оба они равны уклону дна канала io.
Тяжести. При этом потенциальная энергия переходит в кинетическую и кинетическая энергия за счет трения преобразуется в тепло. Из (6.1) также следует, что до тех пор, пока к потоку применимо уравнение Бернулли потери на участке не зависят от шероховатости, а зависят от уклона дна. В открытых руслах, как правило, наблюдается турбулентный режим движения.
где S – площадь сечения, i – геометрический уклон, R – гидравлический радиус, С – коэффициент Шези, зависящий от гидравлического радиуса R и от шероховатости русла. Для коэффициента Шези предложено несколько зависимостей, одна из наиболее простых – формула И.И. Агроскина С = 1/n + 17, 72 lgR, где n – коэффициент шероховатости определяется по таблицам. При расчете открытых каналов встречаются следующие типовые задачи: Задача 1. Заданы: глубина потока h, все геометрические элементы сечения, необходимые для определения гидравлического радиуса R и площади сечения S, коэффициент шероховатости стенок канала n и уклон дня канала i. Определить: расход воды в канале Q. Решение задачи сводится к определению R, S, C и к подстановке их в формулу (6.2). Задача 2. Заданы: расход воды Q, все геометрические параметры кроме глубины, коэффициент шероховатости n и уклон дна канала i0. Определить: глубину потока h. Для определения h необходимо решить уравнение (6.2) с одним неизвестным – h; оно решается на ЭВМ или графоаналитическим методом. Задача 3. Заданы: расход воды Q, все геометрические параметры сечение и глубина, коэффициент шероховатости стенок канала n. Определить уклон дня канала i. Уклон определяется по формуле Шези (6.2)
Некруглого сечения В технике часто применяют вентиляционные каналы прямоугольного или квадратного сечения, нагревательные приборы эллиптического сечения и другие устройства, где живое сечение потока имеет некруглую форму. При рассмотрении равномерного движения в каналах произвольной формы (Кинематика) было введено определение гидравлического радиуса – линейного параметра, определяемого отношением площади живого сечения потока S к его периметру c R = S/ c Для расчетов трубопроводов некруглого сечения применяют понятие эквивалентного диаметра, равного учетверенному значению гидравлического радиуса d Э = 4R = 4 S/ c. С помощью величины dЭ определяют потери энергии, а также другие характеристики движения. В результате применяют расчетные зависимости и формулы для расчета круглых труб и каналов, но вместо диаметра подставляют dЭ. Практически для любого случая расчета трубы некруглого сечения, возможно применить следующий алгоритм: 1. Определяется площадь сечения канала S; 2. Определяется смоченный периметр того же сечения; 3. Находится гидравлический радиус R и эквивалентный диаметр d Э = 4R 4. Значение d Э подставляется во все зависимости (по формулам для круглых труб) вместо d. Например, Задача 7.1. Определить потери давления в вентиляционном канале из листового железа длиной 21 м; сечение прямоугольное со сторонами а ´ в = 300 ´ 400 мм. Массовый расход воздуха Qm = 900кг/ч, плотность воздуха r = 1, 2 кг/м3, кинематический коэффициент вязкости воздуха n = 0, 15 см2/с. Решение. Средняя скорость течения в канале
эквивалентный диаметр и число Рейнольдса Эквивалентная шероховатость поверхности листовой стали – материала канала кЭ = 0, 1 мм. Параметр, определяющий зону сопротивления, подсчитывается так
т.е. имеем переходную зону сопротивления. Коэффициент гидравлического трения
Искомые потери давления определяются по формуле
Фазы гидравлического удара Рассмотрим фазы гидравлического удара при закрытии трубы, по которой жидкость вытекает из открытого резервуара. Пусть в конце горизонтальной трубы, по которой жидкость движется со скоростью V0, произведено мгновенное закрытие крана, рис.9.1.а. При этом скорость частиц жидкости, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдёт в работу деформации стенок трубы и жидкости (стенки растягиваются, а жидкость сжимается). На заторможенные частицы у крана набегают другие, соседние с ними и тоже теряют скорость; в результате сечения n-n перемещается влево со скоростью с, называемой скоростью ударной волны. Сама же переходная область, в которой давление изменяется на величину Δ pуд, называется ударной волной.
Когда ударная волна переместится до резервуара, жидкость окажется остановленной и сжатой во всей трубе, а стенки трубы растянутыми. Ударное повышение давления Δ pуд распространится на всю трубу, рис.9.1.б. Но такое состояние не является равновесным. Под действием перепада давления Δ pуд частицы жидкости устремятся из трубы в резервуар, причём это движение начнётся с сечения, непосредственно прилегающего к резервуару. Теперь сечение n-n перемещается в обратном направлении – к крану – с той же скоростью с, оставляя за собой выровненное давление р0, рис.9.1.в. Жидкость и стенки трубы предполагаются упругими, поэтому они возвращаются к прежнему состоянию, соответствующие давлению р0. Работа деформации полностью переходит в кинетическую энергию и жидкость в трубе приобретает первоначальную скорость V0, но направленную теперь в противоположную сторону. С этой скоростью «жидкая колонна», рис.9.1.г, стремится оторваться от крана, в результате возникает отрицательная ударная волна (P0 - Δ Pуд), которая направлена от крана к резервуару со скоростью c, оставляя за собой сжавшиеся стенки трубы и расширившуюся жидкость, что обусловлено снижением давления, рис.9.1д. Кинетическая энергия жидкости вновь переходит в работу деформаций, но противоположного знака. Состояние трубы в момент прихода отрицательной ударной волны к резервуару показано на рис.9.1.е. Так же как для случая, изображённого на рис.9.1.б, оно не является равновесным. На рис.9.1.ж показан процесс выравнивания давления в трубе и в резервуаре, сопровождающийся возникновением движения жидкости со скоростью V0. Очевидно, что как только отражённая от резервуара ударная волна под давлением Δ pуд достигает крана, возникает ситуация, уже имевшая место в момент закрытия крана. Весь цикл гидравлического удара повторился. После нескольких циклов из-за возникающего при движении трения Δ pуд постепенно уменьшается, и энергия рассеивания. 9.2 Формула Н.Е. Жуковского для Δ p уд Для определения Δ pуд применим второй закон Ньютона в виде
 . .
 или или 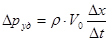 . Величина . Величина
Зависимость (9.4) носит название формулы Жуковского для величины превышения давления при гидравлическом ударе. Скорость распространения ударной волны с зависит от рода жидкости материала, диаметра, толщины стенок трубы и может быть найдена так

где ρ – плотность жидкости, Е0 – модуль упругости жидкости, d – внутренний диаметр трубы, Е – модуль упругости материала стенок трубы, δ – толщина стенок трубы. Для воды при обычных значениях отношения δ /d значения скорости с может приближённо приниматься равным 1200 м/с для стальных труб и 1000 м/с для чугунных. Формула (9.5) справедлива для так называемого прямого гидравлического удара. Гидравлическиё удар называется прямым, если время закрытия запорного устройства меньше времени двойного пробега ударной волны вдоль трубопровода При Гидравлический удар также может иметь место и при быстром открытии задвижки на напорном трубопроводе. В этом случае происходит значительное понижение давления в трубопроводе в результате резкого увеличения скорости. Такой гидравлический удар, характеризующийся понижением давления, носит название отрицательного удара. Сифонный трубопровод Сифонным трубопроводом (сифоном) называется самотечный трубопровод, часть которого располагается выше уровня в сосуде (резервуаре), из которого происходит подача жидкости, рис. 10.1 Сифонные трубопроводы используют, например, в качестве водосбросов гидротехнических сооружений, для слива нефтепродуктов из цистерн, опорожнения водоемов через возвышенности, при самотечном соединении колодцев в системах водоснабжения и т. д. Для того, чтобы сифон начал работать, необходимо заполнить его жидкостью, удалив воздух. Этого можно достичь путем отсасывания воздуха в наивысшей точке сифона или заперев концы сифона, залить его жидкостью через верхнюю точку, где одновременно удаляют воздух. После сплошного заполнения сифона жидкостью он начинает работать как обыкновенная труба, поэтому расчет сифонного трубопровода принципиально ничем не отличается от расчета простого трубопровода. Если составить уравнение Бернулли для сечений 1 – 1 и 2 – 2 взяв за 0 – 0 плоскость отсчета и считать, что в резервуарах жидкость покоится, то получим
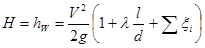
 . .
Принимая V1=0 перепишем последнее уравнение в виде
 . .
Величина в левой части (10.3) представляет собой вакуум
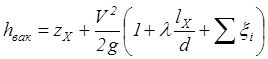 , ,
где V – средняя скорость жидкости в сифоне, zX – высота сечения с давлением pХ над уровнем жидкости в резервуаре 1, lX – длина части сифонной трубы от начала до сечения х – х. Из уравнения (10.4) следует, что hвак будет тем больше, чем больше zX, скорость V и потери напора; предельным местоположением сечения х – х будет наивысшее сечение трубы. Теоретически для нормальной работы сифонного трубопровода необходимо, чтобы минимальное давление в нем было всегда больше упругости паров жидкости при данной температуре
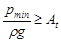 , ,
где pmin – минимальное давление в сифоне, ρ – плотность жидкости, At – упругость паров жидкости в м. ст. жидкости.
Характеристика трубопровода В гидравлических расчетах простых и сложных трубопроводов используют графические методы, которые во многих случаях облегчают решение задач. Эти методы основаны на графическом построении характеристик трубопроводов. Дополнительная часть Моделирование Многие практически важные задачи гидравлики и гидромеханики не поддаются теоретическому решению (по существу ни один из вопросов, касающихся турбулентного движения жидкости, не может быть решен практически); тогда прибегают к исследованию процессов на моделях – так называемому моделированию. Различают три типа моделирования: математическое, аналоговое и физическое. Совокупность уравнений, описывающих физический процесс, называют математической моделью, а изучение его поведения в тех или иных условиях путем решения этих уравнений – математическим моделированием. Математическое моделирование гидравлических явлений возможно осуществлять аналитическими методами, а также методами численного расчета с применением ЭВМ. Явление может исследоваться на основе изучения его модели иной физической природы, если математически они описываются одними и теми же уравнениями. Такое моделирование называют аналоговым. Например, замена натурного фильтрационного потока течением электрического тока по проводнику является аналоговым моделированием (метод ЭГДА). Если модель и моделируемый объект (натура) имеют одну и ту же физическую природу, то такое моделирование называется физическим. Например, исследование обтекания мостовой опоры на малой модели в лаборатории. В дальнейшем будем рассматривать только физическое моделирование. Опыты обычно проводят на малых моделях натурных объектов. Они просты в изготовлении, их малые размеры позволяют осуществлять в лаборатории разнообразные условия опытов и выявлять искомые закономерности. Тем самым исследования на модели приводят к значительной экономии. При моделировании возникает задача об условиях, при которых результаты исследований модельного потока можно перевести на натурный поток; решение этой задачи дает теория математического подобия потоков жидкости. Подобие Различают геометрическое, кинематическое и динамическое подобие потоков; совокупность их составляет механическое подобие потоков жидкости. Геометрическое подобие состоит в том, что все сходственные линейные элементы двух подобных потоков пропорциональны, а соответствующие углы равны. При этом отношение сходственных линейных размеров натуры LH и модели LM одинаково для всех размеров
 , ,
где α L – линейный масштаб. Сходственные площади и объемы также находятся в одном и том же соотношении
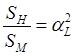 , ,  . .
Одного геометрического подобия недостаточно для того, чтобы модель правильно отражала работу натурного сооружения или потока. Например, движение жидкости в двух геометрически подобных трубах может иметь различный характер – в одной ламинарный, а в другой – турбулентный. Кинематическое подобие состоит в том, что в сходственных точках все кинематические параметры находятся в одинаковом отношении, причем векторные величины имеют соответственно одинаковые направления. Во всех сходственных точках для линейной скорости имеем
 , ,
так же как и для линейного ускорения
 . .
Время прохождения сходственными частицами сходственных расстояний находится (как следствие (2.3) и (2.4)) также в одном и том же соотношении
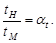
Картины линий тока на натуре и на модели будут по виду тождественны. Условия (2.1) – (2.5) дают связь между масштабными коэффициентами. Например, для масштабного коэффициента скорости α ν
Динамически подобными называются такие потоки, в которых выполняются следующие три условия: 1. В сходственных точках этих потоков действуют силы одной и той же природы. 2. Отношения между одноименными силами во всех сходственных точках потоков равны одной и той же величине. 3. Начальные и граничные условия в этих потоках тождественны и отличаются только масштабом задаваемых параметров. Так как размерностью силы является произведение размерностей массы M = ρ · L3 и ускорения j = L · T –2 , т. е. F = ρ · L3 · L· T-2 = ρ L2 · L2/T2 =ρ · L2 · V2, то для динамического подобия необходимо соблюдение отношения
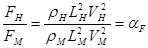 . .
Задача 2.1: Выразить масштабы подобия угловой скорости α ω , объемного расхода α Q, энергии α E и мощности в зависимости от масштаба времени α t, линейного масштаба α L и масштаба плотности α ρ . Решение: Угловая скорость есть отношение радиана ко времени, поэтому ω ~ 1/t. Масштаб подобия угловой скорости будет равен ω Н/ω М = tM/tH = α t-1. Аналогично для расхода Q = V · S ~ L/t · L2 ~ L3/t Задача 2.2: Определить масштаб времени α t, если модель судна, изготовленная в 1/100 натуральной величины, движется в 10 раз медленнее судна. Решение: По условию задачи VH/VM = 10, VH/VM = α L · α t-1. Окончательно α L · α t-1 = 10 и α t = 100/10 = 10. Автомодельность Если какая либо – величина, характеризующая гидравлическое явление не зависит от от какого – либо критерия подобия, то говорят, что она автомодельна по отношению к этому критерию. Например, коэффициент гидравлического сопротивления λ в квадратичной области и коэффициент Шези С не зависят от числа Рейнольдса и поэтому автомодельны по числу Re. При скорости течения газа не превышающих нескольких десятков метров в секунду сжимаемость можно не учитывать и такие течения мохно считать автомодельными по числу Маха. Существование областей автомодельности облегчает моделирование гидравлических явлений, так как делает ненужным удовлетворять некоторым критериям подобия.
Введение В конспекте изложены три темы, обязательные в общем курсе гидравлики. Первая посвящена расчету трубопроводов – основных элементов всех гидравлических сетей и систем и поэтому является важнейшей в смысле практических применений. В последующих двух темах рассматриваются задачи, связанные с истечением жидкостей из отверстий, а также задачи гидродинамического моделирования. Ввиду больших трудностей при изучении течений жидкостей моделирование часто является основным методом исследования. По этой причине подробно рассмотрены многие критерии подобия и связанные с ними примеры решения задач. Для закрепления теоретического материала приведено значительное число задач, решение которых обязательно. Как и в остальных частях конспекта лекций, изложение ведется на двух уровнях: основная часть изложена на первом – низшем уровне. Усвоив этот основной объем, студент может рассчитывать на минимальную положительную оценку на экзамене. Окончательное деление всего материала на части, соответствующие оценкам, может провести преподаватель. Гидравлические расчеты трубопроводов Классификация трубопроводов Трубопроводы нашли исключительно широкое применение в водоснабжении, транспортировке нефти и газа, в системах теплоснабжения, в различных энергетических и двигательных установках. Жидкость движется по трубопроводу вследствие того, что ее потенциальная энергия в начале трубопровода больше, чем в конце. Эта разность потенциальных энергий необходима для преодоления гидравлических сопротивлений между рассматриваемыми сечениями трубопровода. Она может быть создана разными способами: а) работой насоса; б) благодаря разности уровней жидкости – самотечная подача; в) из-за повышенного давления газа на свободную поверхность жидкости в баке – вытеснительная подача. При расчете трубопроводов используются: уравнение неразрывности, уравнение Бернулли, зависимости для расчета сопротивлений и экспериментальные данные. Простыми трубопроводами называют такие, у которых диаметр трубы, а также расход жидкости на всем протяжении остаются неизменными, а сложными – все остальные. Любой сложный трубопровод всегда возможно представить состоящим из ряда простых. |
Последнее изменение этой страницы: 2019-04-09; Просмотров: 271; Нарушение авторского права страницы