Истечение через малое отверстие в тонкой стенке

Рассмотрим истечение жидкости из резервуара через малое отверстие, рис.1.1. Глубина погружения центра отверстия под свободной поверхностью равна Н; часто величина Н называется напором. Истечение происходит при постоянном напоре; это возможно, если в резервуар подаётся такой же расход, какой вытекает из отверстия. Задача состоит в определении скорости и расхода потока жидкости вытекающей из отверстия. Предварительно дадим несколько определений.

+            а)                                     б) Рис1.1.

Малым отверстием называется такое, у которого наибольший вертикальный размер d не превышает 0, 1Н ( d ≤ 0, 1Н ). Траектории частиц жидкости при приближении к отверстию искривляются и за сечением отверстия в свободной струе образует сжатое сечение, рис.1.1.б..

Ближайшее к отверстию сечение струи, в котором движение может быть принято плавно изменяющемся, находится на расстоянии примерно 0.5d от внутренней поверхности стенки резервуара; оно называется сжатым сечением. Стенку можно считать тонкой, если её толщина δ никак не влияет на процесс истечения; в частности полагают, что δ < 0, 2d, d – диаметр отверстия, через которое жидкость вытекает.

Коэффициентом сжатия ε называется отношение площади сжатого сечения S_c к площади отверстия S

(1.1)

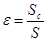
Для решения задачи применим уравнение Бернулли для потока вязкой жидкости к сечениям, движение в которых плавно изменяющееся; такими сечениями является – свободная поверхность в резервуаре 1-1 и сжатое сечение струи 2-2, рис.1.1а. Потери в данном случае происходят за счёт искривления струек и выражаются зависимостью

(1.2)

где V – скорость в сжатом сечении, ξ – коэффициент местных сопротивлений. Из рис.1.1. следует: р₁=р₂=р_ат, V₁=0, V₂≡ V_c, z₁-z₂=H, поэтому уравнение Бернулли ( ) принимает вид

(1.3)

окончательно получаем для скорости

(1.4)

где величина φ

(1.5)

(1.6)

называется коэффициентом скорости и зависимость (1.4) переходит в

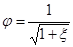
Расход при истечении (с учётом (1.1) и (1.6))

(1.7)

или

Произведение  называется коэффициентом расхода.

Если известны значения ε, φ, S и Н, то возможно найти скорость и расход при истечении; таким образом поставленная задача решена.

При расчёте истечения через отверстие возможны три типа задач:

1. Определение расхода Q при известных напоре Н и площади отверстия S_о.

2. Определение напора Н, необходимого для пропуска заданного расхода Q через отверстие площади S_о.

3. Определение площади отверстия S_о при известных Q и H.

Для обычных условий истечения значения основных коэффициентов полагают такими: μ =0, 60-0, 62; φ =0, 97; ε =0, 61-0, 64; ξ =0, 06.

Задача 1.1 Круглое отверстие диаметром d=15мм в стенке открытой бочки с водой закрыто пробкой. Глубина над центром отверстия равна Н=0, 85м. Определить скорость и расход воды, вытекающий из отверстия сразу же после удаления пробки. Принять μ =0, 60; φ =0, 97.

Решение Все расчёты выполним в системе СИ, поэтому g=9, 81м/с. Скорость истечения определяем по формуле (1.6) V=0, 97^. . Площадь отверстия равна . Расход определяется по зависимости (1.7) Q=0.6^.0.00018^. .

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: