
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Введение в математический анализ.Стр 1 из 5Следующая ⇒
КОМПЛЕКСНЫЕ ЧИСЛА (КЧ) Комплексным числом z называется выражение z = a+bi , где a – действительная часть КЧ или a = Re z. b – мнимая часть КЧ или b = Im z.
0+bi = bi - чисто мнимое число a + 0i = a - действительное число
Z1 = a1 + b1i Z2 = a2 + b2
Действия над КЧ. Z1 Возведение в степень мнимой единицы: i1 = i i2 = – 1 i3 = i i4 = 1 Z1 = (a1 Сопряженным числом (
Пример:
– деление КЧ. Пример:
Комплексная плоскость. Z = a + b Модуль КЧ.
Аргумент КЧ. Аргумент КЧ – Полярная систе
ма координат
Пример:
Примеры:
Формула Эйлера.
КЧ не сравнивают между собой. Множество КЧ не упорядоченно. Возведение в степень КЧ.
При возведении в степень модуль возводиться в эту степень, а аргумент умножается на показатель степени. Формула Муавра.
Возведение во 2 – ю и 3 – ю степень по формуле Муавра:
Извлечение корня из КЧ.
Корень n – ой степени из КЧ имеет n различных значений. Примеры: 1) 2)
Все корни n-ой степени из единицы находятся на единичной окружности и делят эту окружность на n равных частей.
Введение в математический анализ. N – натуральные числа, Q – рациональные(дробные), Z – целые числа R – все действительные M(N) = A0, где M – множество, A0 – алеф нуль. Счетное множество – это множество, элементы которого можно посчитать.
R – несчетное
Множество действительных чисел всюду плотны на всей числовой оси.
(a, b) – открытый
Окр [x0] – окрестность точки x0 , любой открытый промежуток, содержащий x0. Окр [x0] = (a, b), где (a, b) содержит x0 – это окрестность. Кванторы 1) 2) |x – x0| – расстояние от точки x до точки x0 Рисунок. Числовой функцией (f) называется соответствие между числовыми множествами X
y = f (x)
образ x прообраз y
У каждого прообраза всегда один образ, у каждого образа может быть много прообразов. Взаимнооднозначная функция – это когда разные x имеют разные y. Способы задания функций: а) аналитический; б) графический; в) табличный; г) алгоритмический. Функции делятся на 2 класса
Элементарные неэлементарные (специальные) Элементарные функции изучаются в школьной математике и делятся на: 1) Базисные а) Степенные y = xn б) Показательные y = ax в) Тригонометрические y = sin x 2) Остальные: f
f -1 (обратная функция) Обратные показательным – логарифмические функции. Обратные тригонометрическим – arc… Пример:
y = f (g(x)) – сложная функция – композиция элементарных функций. Элементарными функциями называются функции, полученные из элементарных базисных функций с помощью алгебраических операций и операций композиции. Г(f) – график функции. График функции есть множество точек (x, y), где y = f(x). Общие свойства функций: 1) Четность – 2) Нечетность – 3) Периодичность – Рисунок f(x) – ограниченная сверху, если f(x) – ограниченная снизу, если f(x) – ограниченная, если
Если y = f(x), то Д – область определения данной функции. Свойства модулей суммы и разности:
Теория пределов Число b называется пределом функции в точке а, если для любой
Число b называется пределом функции при неограниченном возрастании аргумента y = f(x) = y = f(x) = x2 1) 2) Пример: y = Неопределенности.
Раскрытие неопределенностей. Рис (необязательно). Бесконечно малой величиной при
1) 2) Бесконечно большой величиной при
Любая бесконечно большая величина неограниченна. Разрыв первого рода. Пусть I. Если Примеры: 1)
2) 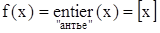 – целая часть числа x. – целая часть числа x.
3)
II. Если 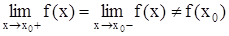 , то в точке , то в точке 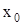 функция испытывает устранимый разрыв первого рода. функция испытывает устранимый разрыв первого рода.
Примеры: 1)
2) 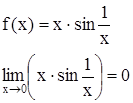
Рисунок.
3)
4) 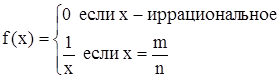
Рисунок. Разрыв второго рода. Функция испытывает разрыв второго рода, если
Свойства функции непрерывной на замкнутом отрезке. Пусть функция
Теорема 1. Функция принимает наибольшее и наименьшее значение на 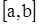 . Или . Или 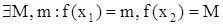 , где , где 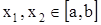 . .
Теорема 2. Функция принимает все свои промежуточные значения на
Теорема 3. Если функция принимает на концах отрезка 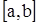 значения разных знаков, то внутри отрезка найдется точка, в которой значения разных знаков, то внутри отрезка найдется точка, в которой 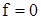 . Или . Или 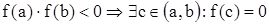 . .
Производная функции. Пусть функция Тогда Производная функции в точке есть предел отношения приращения функции ( Дифференцируемость. Теорема. Доказательство: Пусть Тогда
Это верно при условии, что каждая из функций дифференцируема.
Теорема о производной обратной функции. Теорема. Доказательство: Пусть
Обратная функция существует если Тогда
Производная сложной степенной функции.
Прием логарифмического дифференцирования.
Производная неявной функции.
Теорема Каши о среднем. Доказательство: Пусть
Тогда
F – гладкая на отрезке
Треугольник Паскаля.
Исследование функции. План общего исследования функции. 1. Область определения, четность, периодичность. 2. С помощью пределов выясняем непрерывность, ищем асимптоты. 3. С помощью первой производной – монотонность и экстремумы. 4. С помощью второй производной – выпуклость и вогнутость, точки перегиба. 5. График функции. Монотонность. Функция называется возрастающей если большему значению аргумента соответствует большее значение функции, а меньшему соответствует меньше.
Функция называется убывающей если большему значению аргумента соответствует меньшее значение функции, а меньшему соответствует большее.
Теорема. У возрастающей функции производная больше 0 ( Доказательство:
Экстремумы функции.
Точка Необходимый признак экстремума, если
Если Если Точка, в которой производная, равна нулю, называется критической точкой.
Первый достаточный признак экстремума. Если при переходе через критическую точку производная меняет знак с ”+” на “-“,то в этой точке максимум. Если при переходе через критическую точку производная меняет знак с ”-” на “+“,то в этой точке минимум.
Второй достаточный признак экстремума. Асимптоты
Вертикальные Наклонные Горизонтальные (частный случай наклонной асимптоты) I. Вертикальные асимптоты всегда имеют уравнение Значит
Пример:
Наклонная асимптота Возможные варианты графика функции. Примеры исследования функции: I. 1) 2)
Наклонная асимптота 3)
4)
3)
4)
5)
6)
7)
8)
9) Декартов лист.
Полярные координаты.
КОМПЛЕКСНЫЕ ЧИСЛА (КЧ) Комплексным числом z называется выражение z = a+bi , где a – действительная часть КЧ или a = Re z. b – мнимая часть КЧ или b = Im z.
0+bi = bi - чисто мнимое число a + 0i = a - действительное число
Z1 = a1 + b1i Z2 = a2 + b2
Действия над КЧ. Z1 Возведение в степень мнимой единицы: i1 = i i2 = – 1 i3 = i i4 = 1 Z1 = (a1 Сопряженным числом (
Пример:
– деление КЧ. Пример:
Комплексная плоскость. Z = a + b Модуль КЧ.
Аргумент КЧ. Аргумент КЧ – Полярная систе
ма координат
Пример:
Примеры:
Формула Эйлера.
КЧ не сравнивают между собой. Множество КЧ не упорядоченно. Возведение в степень КЧ.
При возведении в степень модуль возводиться в эту степень, а аргумент умножается на показатель степени. Формула Муавра.
Возведение во 2 – ю и 3 – ю степень по формуле Муавра:
Извлечение корня из КЧ.
Корень n – ой степени из КЧ имеет n различных значений. Примеры: 1) 2)
Все корни n-ой степени из единицы находятся на единичной окружности и делят эту окружность на n равных частей.
Введение в математический анализ. |
Последнее изменение этой страницы: 2019-04-10; Просмотров: 273; Нарушение авторского права страницы