
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Теорема о связи бесконечно малой и бесконечно большой величиной.
Если Если Доказательство: Допустим, что
Следствие: Свойства бесконечно малых величин: 1) Алгебраическая сумма бесконечно малых величин есть бесконечно малая: Доказательство:
2) Произведение бесконечно малой величины на ограниченную функцию есть бесконечно малая: Доказательство:
3) Частное от деления бесконечно малой величины на любую функцию, предел которой не равен 0, есть бесконечно малая: Теоремы о пределах. Теорема 1. Предел суммы равен сумме пределов, если они существуют: Доказательство:
Из теоремы о связи между пределом и бесконечно малой величиной следует:
Получаем Теорема 2. Предел произведения равен произведению пределов, если они существуют: Доказательство:
Из теоремы о связи между пределом и бесконечно малой величиной следует:
Получаем
Теорема 3. Предел частного равен частному пределов: Доказательство:
Из теоремы о связи между пределом и бесконечно малой величиной следует:
Получаем
Теорема 4. Предел сохраняет знак неравенства. Если Доказательство: Следовательно, Следствие:
Теорема 5. Если функция ограниченна и монотонна на (a, b), то она имеет предел: Теорема 6. Критерий Коши. Если тогда и только тогда Приемы раскрытия неопределенностей. 1) Выделение общего множителя (для неопределенности Пример:
2) Умножение на сопряженное выражение (для неопределенности Пример:
3) Выделение главной части (для неопределенности Примеры:
Теорема. Первый замечательный предел Доказательство (геометрическое):
 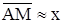
Так как Следствия из теоремы: 1) 2) 3) 4) 5) Теорема. Второй замечательный предел Доказательство: Бином Ньютона.
Используем бином Ньютона для доказательства неравенства:
Отсюда заключаем, что Следствия из теоремы: 1) 2)
4) Доказательство:
Если принять, что
Примеры: 1) Учитывая, что 2)
Учитывая, что
Сравнение б.м.в. Пусть Определение 1. Если Определение 2. Если
Определение 3. Если Следствие из определения 3: Теорема. Если Доказательство: Пусть Тогда
Непрерывность. Определение 1. Пусть функция Определение 2. Функция Определение 3. Функция Приращение аргумента Приращение функции Определение 4. Функция Если функция не является непрерывной в точке Если функция непрерывна на отрезке (a, b), то функция неразрывна на отрезке (a, b). Определение 5. Функция
Определение 5. Функция Функция непрерывна на отрезке Теоремы о непрерывных функциях. Теорема 1. Сложение, умножение, деление непрерывных функций – непрерывны. Доказательство: Пусть Тогда Доказательство для умножения и деления аналогично доказательству для сложения. Теорема 2. Композиция непрерывных функций непрерывна: Функция Теорема 3. Все элементарные функции непрерывны. Разрыв функции. Разрыв первого рода. Пусть I. Если Примеры: 1)
2) 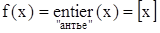 – целая часть числа x. – целая часть числа x.
3)
II. Если 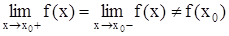 , то в точке , то в точке 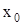 функция испытывает устранимый разрыв первого рода. функция испытывает устранимый разрыв первого рода.
Примеры: 1)
2) 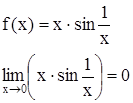 Рисунок.
3)
4) 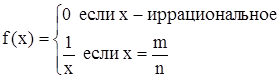
Рисунок. Разрыв второго рода. Функция испытывает разрыв второго рода, если
Свойства функции непрерывной на замкнутом отрезке. Пусть функция
Теорема 1. Функция принимает наибольшее и наименьшее значение на 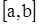 . Или . Или 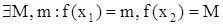 , где , где 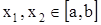 . .
Теорема 2. Функция принимает все свои промежуточные значения на
Теорема 3. Если функция принимает на концах отрезка 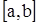 значения разных знаков, то внутри отрезка найдется точка, в которой значения разных знаков, то внутри отрезка найдется точка, в которой 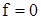 . Или . Или 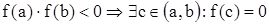 . .
Производная функции. Пусть функция Тогда Производная функции в точке есть предел отношения приращения функции ( Дифференцируемость. |
Последнее изменение этой страницы: 2019-04-10; Просмотров: 1475; Нарушение авторского права страницы