ТРЁХФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.

Под трехфазной симметричной системой ЭДС понимают совокупность трех синусоидальных ЭДС одинаковой частоты и амплитуды, сдвинутых по фазе на 120°. Совокупность трехфазной системы ЭДС и трехфазной нагрузки образует трехфазную цепь. Цепь называют симметричной, если в ней комплексные сопротивления соответствующих фаз одинаковы, т.е. если Z_A=Z_B=Z_C. В противном случае она несимметрична.

Напряжения между линейными проводами U_AB, U_BC, U_CA называют линейными напряжениями. Напряжения между нейтральным проводом и соответствующим линейным проводом U_A, U_B, U_C  называют фазными.

-При соединении обмоток источника в звезду фазное напряжение на обмотках источника Uф=Uл/√3 всегда меньше линейного в √3раз, а фазные токи равны линейным Iф=Iл= . Эти соотношения соблюдаются также и на сопротивлениях фаз нагрузки при соединении нагрузки по схеме «звезда», но только при наличии в схеме нулевого провода, сопротивление которого равно нулю Z N = 0. Если сопротивление нулевого провода Z N отлично от нуля, то при симметричном питании и несимметричной нагрузке фаз Z А ¹   Z В ¹ Z С между нейтральными точками источника N и нагрузки N^I возникает разность потенциалов φ _N ¹ φ_N^I, т.е. = , которую называют «смещением нейтрали» . В этом случае для расчета токов в цепи необходимо знать напряжение смещения нейтрали .

Формула для расчёта напряжения смещения нейтрали U _N ^I _N , записанная на основании метода узловых потенциалов, имеет вид:

         

Если U _N ^I _N известно, то напряжения на фазах нагрузки равны:

U _AN ^I = U_AN – U_N^I_N ,     U_BN^I = U_BN - U_N^I_N ,     U_CN^I = U_CN – U_N^I_N .

Тогда для искомых токов можно записать:

I _A = U_AN^I Y_A ;    I_B = U_BN^I Y_B;      I_C = U_CN^I Y_C .

 За условное положительное направление токов в линейных проводах принято направление в сторону потребителей, а в нейтральном – в сторону источника. 

При соединении обмоток источника треугольником объединяют в одну общую точку начало и конец соответствующих фаз Х и В, У и С, Z и А. При симметричной нагрузке Z_ab=Z_bc=Z_ca =Z ф фазные токи меньше линейных в √3 раз (I_А, I_В, I_С – линейные токи; I _ab , I _bc , I _ca – фазные токи): .

Так как фазные напряжения в треугольнике всегда равны линейным Uф=Uл как на источнике, так и на нагрузке, для фазных токов при симметричной и несимметричной нагрузке можно записать:   .

Линейные токи для нагрузки, соединённой треугольником (схема рис. 4.1.), найдём из 1 -го закона Кирхгофа:

Для узла А: I А+ I са - Iab = 0, I А = I ab - I с a ,

Для узла В: I В+ I ab - I bc = 0, I B = I bc - I ab ,

Для узла С: I С + I bc - l ca = 0, I C = I ca - I bc ,

Задание №1:

Для электрической цепи, схема которой изображена на рис.4.2. определить фазные и линейные токи, активную мощность всей цепи и каждой фазы. Построить векторную диаграмму токов и напряжений на комплексной плоскости.

Исходные данные:

U л = U ф = 220 В. Сопротивления в Ом указаны на схеме Рис.4.2.

Рис.4.2.

Решение: Расчет токов производим комплексным методом. Примем, что вектор линейного напряжения UАв = 220 В; Uвс = 220 е ^{- j 120} В; UсА = 220 е ^{j 120} В.

Определяем фазные токи:

IАв = UAв/ZАв = 220/ 14.1e ^{j 45} = 15.6 e ^{- j 45} = 11 - j11A

IBс = Uвс/ZBс = 220 е ^{- j 120}/ 14.1e ^{j 45} = 15, 6 е ^{- j 165} = -15 - j 4,03 А;

IсА ⁼ UсА/ZcА = 220 е ^{j 120}/14.1e ^{j 45} = 15, 6 е ^{j 75} = 4,03 + j15А;

2. Определяем линейные токи:

   Iа = IAв - IсА = 15,6 e ^{- j 45} - 15,6 e ^{j 75} = 11- j 11 – 4.03 - j 15 = 6,97 – j 26 =

26.9 e ^{- j 75} A .

IB  = IBс - IAв = - 26 + j6,97 = 26,9 е ^{j 165} А;

Iс = IСА – Iвс = 19 + j19 = 26,9 е ^{j 45} А;

3. Определяем активные мощности каждой фазы и всей схемы:

Так как нагрузка фаз одинакова, то достаточно рассчитать активную мощность одной фазы:

Рф = I²ф • Rф = 15, 6² • 10 = 2433, 6 Вт.

Активная мощность Рэ, потребляемая всей схемой (тремя фазами) равна:

Рэ = 3• Рф = 3 • 2433, 6 = 7300, 8 Вт

4. Построим векторную диаграмму токов и напряжений (Рис.4.3.).

I B

       

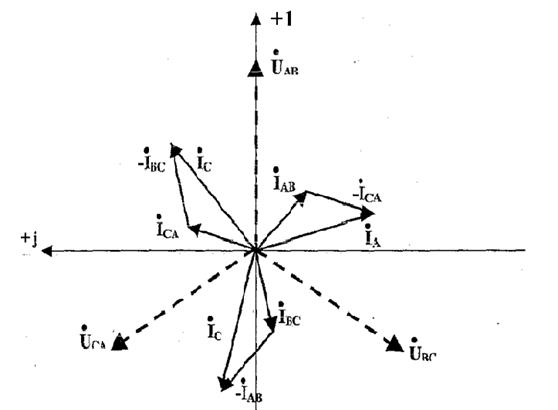
               Рис.4.3.

4. Построим топографическую диаграмму (Рис. 4.4.)

                                            Рис.4.4.

Задание № 2. Для электрической цепи, схема которой изображена

на рис.4.5, определить фазные и линейные токи, ток в нейтральном проводе, активную мощность всей цепи и каждой фазы. Построить векторную диаграмму токов и напряжений на комплексной плоскости.

                        Рис. 4.5.

Исходные данные:       Uл = 220 В,            

Сопротивления в Ом указаны на схеме.                                                                                Решение.

1. Примем, что вектор фазного напряжения UA направлен по вещественной оси, тогда

2. Uа = Uл /√3 = 220 /√3 = 127 В, Uв = 127 e ^{- j 120} В, Uс = 127 е ^{j 120} В

3. Находим линейные (фазные) токи:

IА = UА/ZА ⁼ 127/(3 + j4) = 127/(5е ^{j 53})  = 25,4е ^{- j 53} А.

IB = Uв/Zв = 127 е ^{- j 120} / (3 + j5,2) = 127 е ^{- j 120} /(6 е ^{j 60}) = 21,2е ^{- j 180} а. 

IC = Uс/Zс = 127е ^{j 120}/ (4 + j3) = 127е ^{j 120} / (5е ^{j 37}) = 25,4 е ^{j 83} А.

4. По первому закону Кирхгофа ток в нейтральном проводе равен геометрической сумме линейных тoков:

I0 = IА+Iв +Iс = 25,4 е ^{- j 53} + 21,2 е ^{– j 180} +25,4 е ^{j 83} = 15,24 - j 20,32 -21,2 +3,1+ j 25,15 = -2,86 + j 4,85 = 5,7 е ^{j 122} А.

5. Построим векторную диаграмму напряжений (Рис. 4.6.) и токов (Рис.4.7.)

		Рис.4.6. Векторная диаграмма напряжений.
			Рис.4.7. Векторная диаграмма токов.
	Рис.4.12. Векторная диаграмма напряжений

⇐ Предыдущая123456Следующая ⇒

Поделиться: