Метод Лобачевского при решении алгебраических уравнений

 

Особое место среди нелинейных уравнений занимают алгебраические уравнения или полиномы -ой степени, которые можно представить в виде:

.         (7.5.16)

Для нахождения корней алгебраического уравнения можно использовать методы простой итерации и Ньютона, но, во-первых, эти методы предназначены для отыскания действительных простых корней и, во-вторых, даже если нужно найти только действительные корни необходимо для каждого корня указать интервалы, содержащие изолированные корни и определить начальные приближения.

Для нахождения корней полиномов существует метод Лобачевского. Он не требует определения начальных приближений для корней и позволяет одновременно найти все корни полинома (7.5.16). Недостатком этого метода является тот факт, что при вычислениях приходится иметь дело с числами, которые сильно различаются по порядкам величин.

Пусть коэффициенты полинома (7.5.16)  являются действительными числами, а корни пронумерованы в следующем порядке:

.                        (7.5.17)

Кроме того, будем предполагать, что все корни являются действительными и различными. В основание метода Лобачевского положены следующие соотношения между корнями и коэффициентами алгебраического уравнения (равенства Виетта):

       (7.5.18)

 

Будем говорить, что корни  сильно разделены в смысле отношения их модулей, если модуль предыдущего корня во много раз больше модуля последующего корня:

.                 (7.5.19)

Если выполняются соотношения (7.5.19), то равенства Виетта (7.5.18) значительно упрощаются. Так, первое уравнение в (7.5.18) можно записать в виде:

,

и, так как для корней выполняется соотношение (7.5.19), то все отношения, стоящие в скобках, будут величинами, пренебрежимо малыми в сравнении с единицей, и ими можно пренебречь. Тогда получим

.

Аналогичное будет иметь место и для всех остальных равенств Виетта и (7.5.18) можно заменить следующей системой приближенных равенств, верных лишь в принятой точности вычислений:

                     (7.5.20)

Тогда из (7.5.20) следует, что

. (7.5.21)

Таким образом найти сильно разделенные корни алгебраического уравнения достаточно просто. Поэтому решение уравнения (7.6.16) необходимо начинать с разделения корней. Для этого можно воспользоваться процессом квадрирования, то есть построением последовательности таких полиномов, у которых корни последующего равны квадратам соответствующих корней предыдущего. Это равносильно вычислению коэффициентов для последовательности полиномов по следующим рекуррентным формулам:

(7.5.22)

Процесс квадрирования можно прекратить, если в пределах принятой точности выполняются соотношения:

               (7.5.23)

Тогда для полинома

,   (7.5.24)

в силу разделенности его корней, выполняются соотношения аналогичные (7.5.21), а модули приближенных значений корней исходного уравнения (7.5.16) можно определить из следующих равенств:

(7.5.25)

где , при этом знаки корней определяются подстановкой в исходное уравнение.

Если корни уравнения (7.5.16) все действительные и среди них есть равные по абсолютной величине, например,  и , то для уравнения (7.5.24), полученного после квадрирования, будут справедливы следующие приближенные равенства:

                (7.5.26)

Тогда из второго равенства в (7.5.26) следует, что

а из третьего –

,

и любое из этих равенств можно использовать для определения модулей корней  и , знаки которых, как и ранее, определяются подстановкой в исходное уравнение.

Если уравнение имеет комплексные корни, то они будут попарно сопряжены, так как все коэффициенты уравнения действительные. Пусть, например,  и  – пара комплексно соряженные корней. Эти корни можно представить в виде:

.                   (7.5.27)

Так как  и , то для уравнения (7.5.24), полученного после квадрирования, будут справедливы следующие приближенные равенства:

(7.5.28)

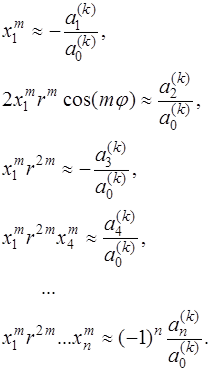
Тогда модуль комплексных чисел можно определить из соотношения:

,                                 (7.5.29)

а для определения аргумента можно воспользоваться первым соотношением Виетта в (7.5.18), которое в данном случае будет иметь вид:

.            (7.5.30)

Отсюда определяется значение , а .

Таким образом, решение алгебраического уравнения методом Лобачевского осуществляется в несколько этапов.

Разделение корней путем квадрирования, при этом по поведению коэффициентов, получаемых в процессе квадрирования, делается вывод о том, какими являются корни уравнения:

· если все коэффициенты стремятся к квадратам соответствующих коэффициентов, полученных на предыдущем шаге процесса квадрирования, то все корни действительные и различные;

· если какой-то коэффициент стремится к квадрату соответствующего коэффициента, деленному на целое число, то номер этого коэффициента указывает на номер первого из равных по модулю корней уравнения в соответствии с нумерацией (7.5.17), а целое число указывает на количество таких корней;

· если какой-то коэффициент меняет знак в процессе квадрирования, то это указывает на наличие комплексно сопряженных корней, причем номер этого коэффициента указывает на первый из таких корней.

2. Вычисление значений корней по формулам, которые соответствуют сделанным выводам о виде корней.

 

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться: