Численное дифференцирование
К численному дифференцированию приходится прибегать в том случае, когда функция 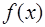 , для которой нужно найти производную, задана таблично или же функциональная зависимость
, для которой нужно найти производную, задана таблично или же функциональная зависимость 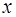 и
и  имеет очень сложное аналитическое выражение. В первом случае методы дифференциального исчисления просто неприменимы, а во втором случае их использование вызывает значительные трудности.
имеет очень сложное аналитическое выражение. В первом случае методы дифференциального исчисления просто неприменимы, а во втором случае их использование вызывает значительные трудности.
В тех случаях, когда численное дифференцирование неприменимо, вместо функции  рассматривают интерполяционный многочлен
рассматривают интерполяционный многочлен  и считают производную от
и считают производную от  приближенно равной производной от
приближенно равной производной от 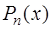 . Естественно, что при этом производная от
. Естественно, что при этом производная от  будет найдена с некоторой погрешностью.
будет найдена с некоторой погрешностью.
Пусть требуется найти производную функции 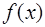 в некоторой точке
в некоторой точке  , если таблица значений функции
, если таблица значений функции  задана в произвольных точках
задана в произвольных точках  . В этом случае наиболее удобным является использование в качестве
. В этом случае наиболее удобным является использование в качестве 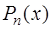 интерполяционного многочлена Ньютона. При этом для построения многочлена Ньютона в качестве первой точки привлекается ближайшая к
интерполяционного многочлена Ньютона. При этом для построения многочлена Ньютона в качестве первой точки привлекается ближайшая к  табличная точка, а затем остальные, в порядке их удаленности от точки
табличная точка, а затем остальные, в порядке их удаленности от точки  . Например, если
. Например, если 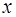 находится вблизи табличной точки
находится вблизи табличной точки  , то для вычисления значения первой производной функции
, то для вычисления значения первой производной функции  в точке
в точке 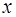 получаются следующие выражения:
получаются следующие выражения:
 (7.3.1)
(7.3.1)
Функцию  можно записать в виде:
можно записать в виде:
 (7.3.2)
(7.3.2)
и, дифференцируя это тождество  раз (в предположении, что
раз (в предположении, что  и
и  имеют производные
имеют производные  -го порядка), имеем
-го порядка), имеем
 . (7.3.3)
. (7.3.3)
Так как за приближенное значение  принимается
принимается  , то погрешность дифференцирования есть
, то погрешность дифференцирования есть  . При замене
. При замене  интерполяционным многочленом предполагается, что остаточный член
интерполяционным многочленом предполагается, что остаточный член  мал, но из этого вовсе не следует, что мало
мал, но из этого вовсе не следует, что мало  , так как производные от малой функции могут быть весьма велики. На самом деле практика показывает, что при таком способе вычисления производных
, так как производные от малой функции могут быть весьма велики. На самом деле практика показывает, что при таком способе вычисления производных 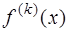 получается сравнительно большая погрешность, особенно при вычислении производных высших порядков.
получается сравнительно большая погрешность, особенно при вычислении производных высших порядков.
Если табличные значения являются равноотстоящими, то есть  , то для вычисления значения первой производной в точке
, то для вычисления значения первой производной в точке 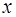 , лежащей вблизи табличной точки
, лежащей вблизи табличной точки 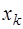 , получаются следующие выражения:
, получаются следующие выражения:
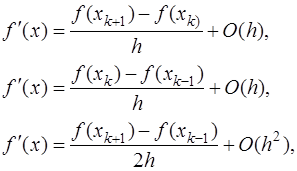 (7.3.4)
(7.3.4)
где  используются для обозначения выражений, имеющих порядок малости, превышающий величины
используются для обозначения выражений, имеющих порядок малости, превышающий величины  и
и  соответственно. Несмотря на то, что с помощью последнего выражения в (7.3.4) получается более точный результат, использовать это выражение для вычисления первой производной нужно с большой осторожностью, так как достаточно часто это приводит к потере устойчивости решения.
соответственно. Несмотря на то, что с помощью последнего выражения в (7.3.4) получается более точный результат, использовать это выражение для вычисления первой производной нужно с большой осторожностью, так как достаточно часто это приводит к потере устойчивости решения.
Для вычисления второй производной в случае, если точка  находится вблизи табличной точки
находится вблизи табличной точки  , используется следующее выражение:
, используется следующее выражение:
 . (7.3.5)
. (7.3.5)
Аналогично можно получить выражения для вычисления производных и более высоких порядков. Кроме того, можно использовать и другие подходы для вычисления значений производных функций, заданных таблично, например, метод неопределенных коэффициентов.
Заметим, что замена производных разностными отношениями типа (7.3.4) и (7.3.5) часто используется при моделировании задач математической физики.
Численное интегрирование
Будем рассматривать задачу вычисления интеграла при помощи некоторого числа значений интегрируемой функции. Достоинство этого метода состоит в его простоте и универсальности.
Пусть  есть любой конечный или бесконечный отрезок числовой оси и требуется найти приближенное значение интеграла
есть любой конечный или бесконечный отрезок числовой оси и требуется найти приближенное значение интеграла
 (7.4.1)
(7.4.1)
по  значениям функции
значениям функции  в точках
в точках  . Многие правила численного интегрирования основаны на замене интегрируемой функции
. Многие правила численного интегрирования основаны на замене интегрируемой функции 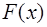 на всем отрезке
на всем отрезке  или на его частях на более простую функцию, близкую к
или на его частях на более простую функцию, близкую к  , легко интегрируемую точно и принимающую в точках
, легко интегрируемую точно и принимающую в точках  те же значения, что и
те же значения, что и  . В качестве такой функции достаточно часто используют алгебраический многочлен или рациональную функцию. В том случае, если интегрируемая функция
. В качестве такой функции достаточно часто используют алгебраический многочлен или рациональную функцию. В том случае, если интегрируемая функция 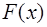 является достаточно гладкой, то можно рассчитывать хорошо приблизить ее многочленом невысокой степени или несложной рациональной функцией. Если же сама функция
является достаточно гладкой, то можно рассчитывать хорошо приблизить ее многочленом невысокой степени или несложной рациональной функцией. Если же сама функция  имеет особенности, то это затруднит такое приближение или сделает его вообще невозможным. В этом случае заранее освобождаются от этих особенностей путем их выделения. Для этого функцию
имеет особенности, то это затруднит такое приближение или сделает его вообще невозможным. В этом случае заранее освобождаются от этих особенностей путем их выделения. Для этого функцию  представляют в виде произведения двух функций:
представляют в виде произведения двух функций:
 , (7.4.2)
, (7.4.2)
где  имеет те же особенности, что и
имеет те же особенности, что и  , и называется весовой функцией или весом, а
, и называется весовой функцией или весом, а  является достаточно гладкой функцией. Тогда задача заключается в вычислении интеграла вида:
является достаточно гладкой функцией. Тогда задача заключается в вычислении интеграла вида:
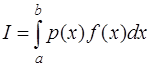 . (7.4.3)
. (7.4.3)
Правила вычисления интегралов в большинстве своем являются специализированными, предназначенными для численного интегрирования функций, имеющих те же особенности, что и весовая функция  . Поэтому при вычислении интеграла (7.4.3) функция
. Поэтому при вычислении интеграла (7.4.3) функция  считается фиксированной функцией, а
считается фиксированной функцией, а  – любой достаточно гладкой функцией на
– любой достаточно гладкой функцией на 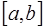 .
.

