Аппроксимация данных методом наименьших квадратов
Пусть 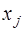 – узлы исходной таблицы данных, а
– узлы исходной таблицы данных, а  – значения экспериментальных данных или некоторой неизвестной функции в узловых точках. Введем непрерывную функцию
– значения экспериментальных данных или некоторой неизвестной функции в узловых точках. Введем непрерывную функцию  для аппроксимации дискретных значений
для аппроксимации дискретных значений  и обозначим
и обозначим
 ,
,
отклонения в узлах 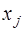 . Тогда сумма квадратов отклонений аппроксимирующей функции
. Тогда сумма квадратов отклонений аппроксимирующей функции  от неизвестной функции
от неизвестной функции  в узловых точках
в узловых точках  ,
, 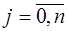 запишется в виде:
запишется в виде:
 . (7.2.66)
. (7.2.66)
Метод построения аппроксимирующей функции 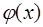 из условия минимизации суммы квадратов отклонений
из условия минимизации суммы квадратов отклонений  называется методом наименьших квадратов (МНК).
называется методом наименьших квадратов (МНК).
Наиболее часто аппроксимирующую функцию  задают в виде:
задают в виде:
 , (7.2.67)
, (7.2.67)
где 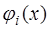 ,
,  ,
,  - линейно независимые базисные функции,
- линейно независимые базисные функции,  - неизвестные коэффициенты, определяемые из условия минимума
- неизвестные коэффициенты, определяемые из условия минимума 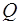 , т. е. из условий равенства нулю частных производных
, т. е. из условий равенства нулю частных производных  по
по  :
:
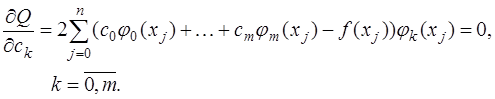 (7.2.68)
(7.2.68)
Таким образом, получаем систему линейных алгебраических уравнений вида  для определения коэффициентов
для определения коэффициентов  ,
, 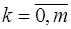 . Эта система называется системой нормальных уравнений. Матрица системы имеет вид
. Эта система называется системой нормальных уравнений. Матрица системы имеет вид
 (7.2.69)
(7.2.69)
и называется матрицей Грама.
Элементами матрицы Грама являются скалярные произведения базисных функций:
 . (7.2.70)
. (7.2.70)
Вектор свободных членов системы нормальных уравнений имеет вид:
 , (7.2.71)
, (7.2.71)
элементами этого вектора являются скалярные произведения
 . (7.2.72)
. (7.2.72)
Матрица Грама обладает следующими основными свойствами:
1) она симметрична, что позволяет сократить объем вычислений при заполнении матрицы;
2) матрица является положительно определенной, поэтому при решении системы нормальных уравнений методом исключения Гаусса можно отказаться от процедуры выбора главного элемента, а сразу брать в качестве ведущего диагональный элемент;
3) определитель матрицы Грама отличен от нуля, если в качестве базиса выбраны линейно независимые функции  .
.
Для аппроксимации экспериментальных данных, определенных с погрешностью  в каждой узловой точке, обычно сначала функцию
в каждой узловой точке, обычно сначала функцию 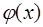 задают в виде линейной комбинации из одной или двух базисных функций и, если после определения коэффициентов
задают в виде линейной комбинации из одной или двух базисных функций и, если после определения коэффициентов  окажется, что
окажется, что  , то расширяют базис добавлением новых функций
, то расширяют базис добавлением новых функций  , так до тех пор, пока не выполнится условие
, так до тех пор, пока не выполнится условие  .
.
Выбор конкретных базисных функций зависит от свойств аппроксимируемой функции  таких, как периодичность, экспоненциальный или логарифмический характер, свойства симметрии, наличие асимптотики и т.д.
таких, как периодичность, экспоненциальный или логарифмический характер, свойства симметрии, наличие асимптотики и т.д.
Аппроксимация алгебраическими полиномами
Пусть аппроксимирующая функция задана в виде алгебраического полинома степени  :
:
 , (7.2.73)
, (7.2.73)
или
 .
.
Степень полинома  выбирают обычно меньше
выбирают обычно меньше  . Аппроксимирующая кривая в этом случае не проходит через экспериментальные точки, т.е. экспериментальные данные «сглаживаются» с помощью функции
. Аппроксимирующая кривая в этом случае не проходит через экспериментальные точки, т.е. экспериментальные данные «сглаживаются» с помощью функции  . Если взять
. Если взять  , то
, то  совпадает с многочленом Лагранжа, аппроксимирующая кривая пройдет через все экспериментальные точки и
совпадает с многочленом Лагранжа, аппроксимирующая кривая пройдет через все экспериментальные точки и  . Это обстоятельство часто используется для отладки и тестирования программ, реализующих алгоритмы МНК.
. Это обстоятельство часто используется для отладки и тестирования программ, реализующих алгоритмы МНК.
Матрица  системы нормальных уравнений и вектор свободных членов для функции
системы нормальных уравнений и вектор свободных членов для функции 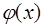 вида (7.2.73) записываются следующим образом:
вида (7.2.73) записываются следующим образом:
 , (7.2.74)
, (7.2.74)
 , (7.2.75)
, (7.2.75)
Для решения систем уравнений с матрицей Грама разработаны методы сингулярного разложения. Если же  , то такие системы можно решать и более простым методом исключения Гаусса.
, то такие системы можно решать и более простым методом исключения Гаусса.
Система нормальных уравнений обычно бывает плохо обусловленной, что приводит к дополнительным сложностям при реализации МНК: вычисление с двойной (расширенной) точностью, введение весовых коэффициентов и т.д. Весовые коэффициенты выбираются из различных соображений, например, полагают:
 ,
, 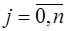 .
.
Такой выбор весовых коэффициентов называется методом статистического взвешивания.
В этом случае:
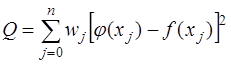
и скалярные произведения в матрице 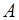 и векторе
и векторе  будут соответственно иметь вид
будут соответственно иметь вид

Аппроксимация ортогональными полиномами
Лучшие по точности результаты при аппроксимации можно получить, если использовать в качестве базисных функций  классические ортогональные полиномы Чебышева, Лежандра, Лагерра, Якоби и других.
классические ортогональные полиномы Чебышева, Лежандра, Лагерра, Якоби и других.
Полиномы называются ортогональными, если существует некоторый интервал 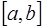 , на котором
, на котором
 , (7.2.76)
, (7.2.76)
где  - весовая функция.
- весовая функция.
В случае большого количества узлов  на
на 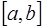 значения интегралов (7.2.76) будут близки к дискретным скалярным произведениям (7.2.70), так как интегрирование можно приближенно заменить суммированием. В этом случае недиагональные элементы матрицы Грама будут небольшими по абсолютной величине, что уменьшает погрешность решения системы нормальных уравнений.
значения интегралов (7.2.76) будут близки к дискретным скалярным произведениям (7.2.70), так как интегрирование можно приближенно заменить суммированием. В этом случае недиагональные элементы матрицы Грама будут небольшими по абсолютной величине, что уменьшает погрешность решения системы нормальных уравнений.
Для наиболее гладкого представления экспериментальных данных (с минимальным числом и амплитудой выбросов) в качестве базисных функций 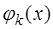 выбирают ортогональные полиномы Чебышева
выбирают ортогональные полиномы Чебышева  , которые определены и ортогональны на интервале
, которые определены и ортогональны на интервале 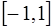 с весовой функцией
с весовой функцией  .
.
Для задания полиномов Чебышева используется рекуррентная формула:
 , (7.2.77)
, (7.2.77)
где  ,
,  .
.
Так как в многочленах Чебышева коэффициент при старших степенях  равен
равен  , то это не всегда удобно при оценке вклада в аппроксимирующую функцию
, то это не всегда удобно при оценке вклада в аппроксимирующую функцию  старших степеней
старших степеней 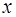 по величине коэффициентов
по величине коэффициентов  . В этом случае полиномы Чебышева можно ввести и по другой рекуррентной формуле, позволяющей построить приведенные многочлены Чебышева:
. В этом случае полиномы Чебышева можно ввести и по другой рекуррентной формуле, позволяющей построить приведенные многочлены Чебышева:
 , (7.2.78)
, (7.2.78)
где  ,
,  .
.
Полиномы  ортогональны на интервале
ортогональны на интервале  с такой же весовой функцией, что и
с такой же весовой функцией, что и  .
.
Весовую функцию, равную единице на интервале  , имеют полиномы Лежандра, которые определяются по следующей рекуррентной формуле:
, имеют полиномы Лежандра, которые определяются по следующей рекуррентной формуле:
 , (7.2.79)
, (7.2.79)
где 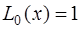 ,
,  .
.
Интервал [ 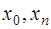 ], где заданны узлы таблицы данных
], где заданны узлы таблицы данных  , переводится в интервал
, переводится в интервал  , где определены и ортогональны полиномы Чебышева и Лежандра с помощью линейного преобразования:
, где определены и ортогональны полиномы Чебышева и Лежандра с помощью линейного преобразования:
 . (7.2.80)
. (7.2.80)
Аппроксимация ортогональными полиномами
дискретной переменной
Если построить систему базисных функций  таким образом, чтобы обращались в нуль скалярные произведения на дискретном множестве узловых точек, то матрица Грама будет диагональной и можно избежать численного решения системы нормальных уравнений. В зависимости от распределения погрешности обрабатываемых данных можно построить ортогональные полиномы дискретной переменной с соответствующими дискретными весовыми функциями
таким образом, чтобы обращались в нуль скалярные произведения на дискретном множестве узловых точек, то матрица Грама будет диагональной и можно избежать численного решения системы нормальных уравнений. В зависимости от распределения погрешности обрабатываемых данных можно построить ортогональные полиномы дискретной переменной с соответствующими дискретными весовыми функциями 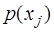 ,
,  . Из классических ортогональных полиномов дискретной переменной известны полиномы Хана, Мейкснера, Кравчука, Шарлье.
. Из классических ортогональных полиномов дискретной переменной известны полиномы Хана, Мейкснера, Кравчука, Шарлье.
Рассмотрим алгоритм построения полиномов Чебышева 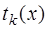 дискретной переменной, которые являются частным случаем полиномов Хана с единичной весовой функцией.
дискретной переменной, которые являются частным случаем полиномов Хана с единичной весовой функцией.
Полагаем:
 (7.2.81)
(7.2.81)
 , (7.2.82)
, (7.2.82)
и неизвестный коэффициент  определим из условия ортогональности
определим из условия ортогональности  и
и  , то есть
, то есть

или
 . (7.2.83)
. (7.2.83)
Откуда
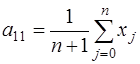 . (7.2.84)
. (7.2.84)
Полином второй степени также представляется в общем виде с неопределенными коэффициентами 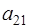 и
и  :
:
 . (7.2.85)
. (7.2.85)
Коэффициенты 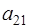 и
и  найдем из условия ортогональности полиномов
найдем из условия ортогональности полиномов  , то есть
, то есть  ,
,  и т.д.
и т.д.
Для полиномов Чебышева дискретной переменной существует двухслойная рекуррентная формула, по которой можно вычислить полином любой степени, зная  :
:
 , (7.2.84)
, (7.2.84)
где
 (7.2.85)
(7.2.85)
Аппроксимирующая функция  определяется, как и ранее, в виде линейной комбинации базисных функций, в качестве которых берутся полиномы Чебышева дискретной переменной
определяется, как и ранее, в виде линейной комбинации базисных функций, в качестве которых берутся полиномы Чебышева дискретной переменной  :
:
 . (7.2.86)
. (7.2.86)
Тогда, так как матрица Грама является диагональной, коэффициенты  этой линейной комбинации определяются как частное от деления правых частей получающейся системы нормальных уравнений на диагональные элементы этой матрицы, то есть:
этой линейной комбинации определяются как частное от деления правых частей получающейся системы нормальных уравнений на диагональные элементы этой матрицы, то есть:
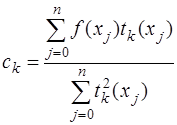 . (7.2.87)
. (7.2.87)
Заметим, что если для улучшения качества аппроксимации возникает необходимость в увеличении числа базисных функций, то не придется пересчитывать коэффициенты  , определенные с меньшим значением
, определенные с меньшим значением 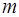 .
.
На практике достаточно часто при обработке экспериментальных данных можно ограничиться построением линейной аппроксимирующей функции (линии регрессии), то есть:
 .
.
Для коэффициентов  и
и 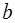 из общего алгоритма МНК получаются выражения:
из общего алгоритма МНК получаются выражения:
 ,
,  ,
,
где
 ,
,  .
.
Погрешность вычисления коэффициентов  и
и 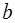 определяется по формулам:
определяется по формулам:
 ,
,
 ,
,
где 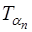 – коэффициент Стьюдента для
– коэффициент Стьюдента для  измерений и доверительной вероятности
измерений и доверительной вероятности  .
.

