Интерполяционные квадратурные формулы

 

Пусть  – достаточно гладкая функция, а интервал  – конечный и замкнутый. Правило вычисления интеграла будем задавать в виде:

.    (7.4.4)

Такое правило называется методом механических квадратур, сумма – квадратурной суммой; ,  – квадратурными коэффициентами; ,  – квадратурными узлами.

Функцию 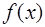 можно приблизить интерполяционным многочленом Лагранжа, который строится по заданным значениям 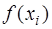, , 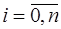то есть

,                         (7.4.5)

где

,       (7.4.6)

,                        (7.4.7)

,     (7.4.8)

 – некоторая точка интервала .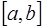

Тогда

(7.4.9)

и

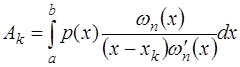,             (7.4.10)

.     (7.4.11)

Квадратурное правило, коэффициенты которого вычисляются согласно (7.4.10), называется интерполяционным. Оно является точным для всех алгебраических многочленов степени не выше n. Поэтому степень точности интерполяционного квадратурного правила равна n.

Частным случаем интерполяционного квадратурного правила является квадратурное правило Ньютона-Котеса. Это правило используется в том случае, когда  является достаточно гладкой функцией и узлы квадратурного правила ,  являются равноотстоящими. В этом случае считают весовую функцию  и квадратурное правило (7.4.4) записывают в виде:

.                    (7.4.12)

Коэффициенты  в (7.4.12), учитывая выражение для  (7.4.10), вычисляются по формуле:

    (7.4.13)

и имеют следующие конкретные значения:

, ,

, ,

, , ,

, ,

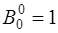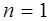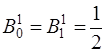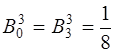и т.д.

Коэффициенты 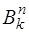 вычислены до . Они являются рациональными числами и обладают следующими свойствами:

1) при каждом n , в чем легко убедиться, если в (7.4.12) положить ;

2) ;

3) при 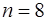 и для всех  среди  встречаются отрицательные, причем абсолютные величины  быстро растут с ростом .

Последнее свойство коэффициентов  является существенным при определении погрешности вычисления интеграла с помощью квадратурной суммы. Так, если значения подынтегральной функции 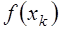,  известны с абсолютной погрешностью , то неустранимая погрешность вычисления интеграла в (7.4.12) может быть оценена величиной

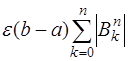,                             (7.4.14)

при этом значения  при увеличении n быстро растут. Например, при  эта сумма равна 560. Поэтому при больших значениях  незначительные ошибки в значениях функций ,  могут привести к большой погрешности в квадратурной сумме (7.4.12). В связи с этим формулы Ньютона-Котеса используются только при малых значениях . Для уменьшения погрешности результата отрезок  разбивают на достаточно большое число m интервалов, затем к каждому из них применяют квадратурную формулу с малым числом узлов, и результаты суммируют. При этом, так как погрешность метода для формулы Ньютона-Котеса можно представить в ви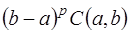де , где  – медленно изменяющаяся функция на , а погрешность той же формулы, применённой к отрезку, полученному делением интервала 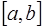 на m частей, есть , то после суммирования погрешность результата примет вид: 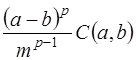. Таким образом, в результате разбиения интервала интегрирования на m частей погрешность результата уменьшается в  раз.

Заметим, что если средняя точка интервала  является узлом квадратурного правила, то алгебраическая точность правила увеличивается на единицу, то есть правило становится точным для многочленов степени

Приведем конкретные формулы Ньютона-Котеса для 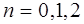, которые используются чаще всего. При этом приведем сразу обобщенные формулы, полученные делением интервала  на  частей и суммированием результатов. При получении формулы для погрешности в случае, когда квадратурный узел является серединой интервала интегрирования, строится интерполяционный многочлен на порядок выше при условии равенства первых производных интерполяционного многочлена и подынтегральной функции в средней точке каждого интервала, полученного при делении. Кроме того, для записи обобщенных квадратурных формул будем использовать следующее обозначение: , .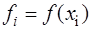

 

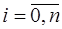Квадратурные формулы прямоугольников ( ).

На интервале  необходимо выбрать одну любую точку в качестве узла квадратурного правила. Обычно выбирают среднюю или крайние точки: левую или правую, и в соответствии с этим получают следующие формулы:

1) формула левых прямоугольников:

,    (7.4.15)

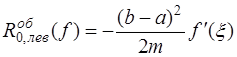,              (7.4.16)

2) формула правых прямоугольников:

,     (7.4.17)

,                 (7.4.18)

3) формула средних прямоугольников:

, (7.4.19)

.                     (7.4.20)

В (7.4.19) .

Квадратурная формула трапеций :

, (7.4.21)

          (7.4.22)

Квадратурная формула Симпсона :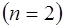

(7.4.23)

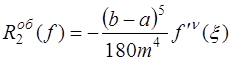.               (7.4.24)

При использовании квадратурной формумы Симпсона значение  должно быть четным.

В порядке убывания точности вычисления интеграла квадратурные формулы Ньютона-Котеса при фиксированном  располагаются в следующем порядке: формула Симпсона, средних прямоугольников, трапеций, крайних прямоугольников.

Обычно требуется вычислить значение интеграла с некоторой заданной точностью . В этом случае строится последовательность значений интеграла 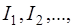 для которой справедливо соотношение:

,                           (7.4.25)

где  – значение интеграла, вычисленное на 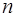-ом шаге. Тогда интеграл считается вычисленным с заданной точностью , если для некоторого шага  будет справедливо неравенство:

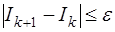.                             (7.4.26)

Для формул Ньютона-Котеса  соответствует значению интеграла, вычисленному при некотором значении ,  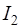– значению интеграла, вычисленному при увеличении значения  в два раза и т.д. При этом, так как узлы квадратурного правила Ньютона-Котеса являются равноотстоящими, то увеличение  в два раза приведет просто к добавлению к старым узлам новых. Поэтому можно организовать процесс вычисления интеграла таким образом, чтобы не пересчитывать полученные ранее значения подынтегральной функции, а только добавлять в квадратурную сумму новые значения.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: