
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Раздел 1 – расчет статически определимых системСтр 1 из 10Следующая ⇒
СТРОИТЕЛЬНАЯ МЕХАНИКА РАСЧЁТ СТЕРЖНЕВЫХ СИСТЕМ Раздел 1 – расчет статически определимых систем Составитель: профессор В.П. ВАЛУЙСКИХ Для студентов 3-го курса специальностей ПГС и ГСХ Слайды разработаны на основе монографий: Киселёв В.А. Строительная механика. Общий курс. – М.: Стройиздат, 1986. – 520 с. 2. Мухин Н.В. Статика сооружений в примерах. – М.: Высшая школа, 1979. - 304 с. СОДЕРЖАТЕЛЬНАЯ И ТЕМАТИЧЕСКАЯ СТРУКТУРА КУРСА ( Ч а с т ь 1 )
Лекции 2-4 |
Кинематический анализ сооружений Основы расчёта на подвижную нагрузку | ||||||||||
| 3 | |||||||||||
| 4 | |||||||||||
| 5 | Лекция 5 | Расчёт шарнирно-консольных балок | |||||||||
| 6 |
Лекции 6-8 |
Расчёт статически определимых ферм | |||||||||
| 7 | |||||||||||
| 8 | |||||||||||
| 9 |
Лекции 9-10 |
Расчёт трехшарнирных арок | |||||||||
| 10 | |||||||||||
| 11 |
Лекции 11-13 |
Основные теоремы об упругих системах. Определение перемещений | |||||||||
| 12 | |||||||||||
| 13 | |||||||||||
| 14 | Лекция 14 | Расчёт статически определимых рам | |||||||||
| 15 | Лекция 15 | Основы расчёта статически неопределимых систем | |||||||||
| 16 |
Лекции 16-17 |
Расчёт статически неопределимых систем методом сил | |||||||||
| 17 |
МЕТОДИЧЕСКОЕ (МУЛЬТИМЕДИЙНОЕ) ОБЕСПЕЧЕНИЕ КУРСА
| № п. п. |  Тема цикла лекций Слайды Тема цикла лекций Слайды
| |
| Лекция 1 | В в е д е н и е 4-7 | |
Лекции 2-4
Кинематический анализ сооружений 8-15
Основы расчёта на подвижную нагрузку 16-21
Лекции 6-8
Расчёт статически определимых ферм 27-38
Лекции 9-10
Расчёт трехшарнирных арок 39-48
Лекции 11-13
Основные теоремы об упругих системах. 49-52
Определение перемещений
Лекции 16-17
Расчёт статически неопределимых систем 60-76
методом сил
Л е к ц и я 1
Введение в курс «Строительная механика»
 Обсуждаемые вопросы (план лекции )
Обсуждаемые вопросы (план лекции )
Предмет и задачи строительной механики
Понятие о расчётной схеме.
Классификация плоских систем
Виды нагрузок и воздействий
Методы расчёта строительных конструкций
Расчётные схемы опор плоских систем
Принцип независимости действия внешних сил
Классификация плоских стержневых систем
 Предмет и задачи строительной механики
Предмет и задачи строительной механики
 Понятие о расчётной схеме
Понятие о расчётной схеме
 |
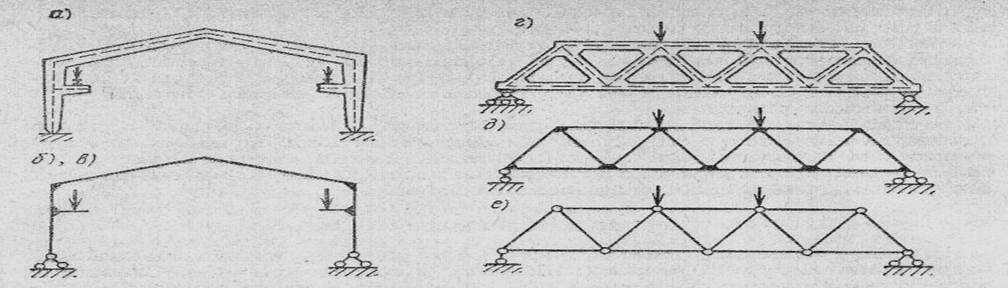



 Р а м а Плоские Ф е р м а
Р а м а Плоские Ф е р м а
 |  |  |
Арк а – комбинированная система Пространственная рама Складчатая система Подпорная стенка
 Виды нагрузок и воздействий
Виды нагрузок и воздействий



Силовые нагрузки + Температурные воздействия + Осадка опор


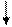












 F ∆ t в > ∆ t н
F ∆ t в > ∆ t н










 ∆
∆ 

 Методы расчёта строительных конструкций
Методы расчёта строительных конструкций

 Расчёт по допускаемым напряжениям Расчёт по предельным состояниям
Расчёт по допускаемым напряжениям Расчёт по предельным состояниям
σ ≤ [σ] = σоп / k * 1 группа – по потере несущей способности
или не пригодности к эксплуатации
Расчёт по допускаемым нагрузкам 2 группа – по не пригодности к
 нормальной эксплуатации
нормальной эксплуатации
F = Р ≤ [Р] = Роп / k *


 Расчётные схемы опор плоских систем
Расчётные схемы опор плоских систем
П Р И З Н А К И К Л А С С И Ф И К А Ц И И
Л е к ц и я 2
Примеры кинематического анализа стержневых систем - ферм


Л е к ц и я 3-5
НА ПОДВИЖНУЮ НАГРУЗКУ
 Обсуждаемые вопросы (план лекции)
Обсуждаемые вопросы (план лекции)
Линии влияния и их форма
Линии влияния и их форма

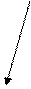


 у= f (х) Траектория движения силы
у= f (х) Траектория движения силы


 у F =1
у F =1










 А х
А х







 В
В
 RA х RB
RA х RB


 la l lb
la l lb

 1
1
 |
 Л . в . RA
Л . в . RA


 1
1
 Л . в . R В
Л . в . R В

 ∑ mB = 0 → RA* l - F* ( l -х) = 0 → RA = F* ( l -х)/ l = ( l -х)/ l RA = ( l -х)/ l
∑ mB = 0 → RA* l - F* ( l -х) = 0 → RA = F* ( l -х)/ l = ( l -х)/ l RA = ( l -х)/ l
∑ m А = 0 → R В* l - F* х = 0 → R В = F* х / l = х/ l R В = = х/ l
 Построение линий влияния в простой шарнирной балке
Построение линий влияния в простой шарнирной балке
Рис. 1
 Классификация балок, входящих в состав ШКБ
Классификация балок, входящих в состав ШКБ
· Основные балки – (балки 1-2 и 7-9)
· Вспомогательные балки - (балки 2-3-4 и 4-5-6)
· Подвесные пролеты - (балка 6-7)
 Построение поэтажных схем
Построение поэтажных схем
 Рис. 2
Рис. 2
 Рис. 3
Рис. 3
Рис. 4
 Расчёт шарнирно-консольных балок на неподвижную нагрузку
Расчёт шарнирно-консольных балок на неподвижную нагрузку
 Расчёт шарнирно-консольных балок на неподвижную нагрузку
Расчёт шарнирно-консольных балок на неподвижную нагрузку
Л е к ц и я 6-8
РАСЧЁТ ПЛОСКИХ
СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ ФЕРМ
 Обсуждаемые вопросы (план лекции)
Обсуждаемые вопросы (план лекции)
Основные понятие о фермах
Терминология
Классификация ферм
4. Статический метод определения усилий в стержнях ферм
от неподвижной нагрузки – способ вырезания узлов
5. Статический метод определения усилий в стержнях ферм
от неподвижной нагрузки – способ сечений (способ Риттера)
Основные понятия о фермах


Терминология





 Верхний пояс Решётка Грузовой пояс
Верхний пояс Решётка Грузовой пояс
Высота фермы Н
 |  |  |  | ||||

 Нижний пояс
Нижний пояс
d – Панель фермы



 l – Пролёт фермы
l – Пролёт фермы
 |
Классификация ферм
Л е к ц и я 9-10
РАСЧЁТ ПЛОСКИХ
СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ АРОК
 Обсуждаемые вопросы (план лекции)
Обсуждаемые вопросы (план лекции)
Типы трехшарнирных арок
Ключевой шарнир
 Левая полуарка С Правая полуарка
Левая полуарка С Правая полуарка

у Внешнее ребро



 Пятовый шарнир
Пятовый шарнир 
 Пятовый шарнир
Пятовый шарнир
 Внутреннее ребро
Внутреннее ребро
f - Стрела подъём арки
 А В
А В
















 х
х
l а l в

L – Пролет арки

F / l - Подъём подъёма
Типы трехшарнирных арок


Простая трехшарнирная арка (ТША) Ползучая ТША


ТША с затяжкой ТША с повышенной затяжкой
 Аналитический расчёт ТША на неподвижную нагрузку
Аналитический расчёт ТША на неподвижную нагрузку


 у
у
 | |||||
 | |||||
 | |||||



 θ
θ


 Q ар f
Q ар f
M ар
N ар
 х
х

l 
Определение опорных реакций
∑ mB = 0 → RA* l - ∑ Fi * а i = 0 → RA = …
∑ m А = 0 → R В* l - ∑ Fi * в i = 0 → R В = …
∑ m С лев = 0 → Н A* f - RA* l + ∑ Fi * ( lA - а i ) = Н A* f – МСб = 0 → Н A = МСб / f
 ∑ m С лев = 0 → НВ* f - R В* l + ∑ Fi * ( l В - в i ) = Н A* f – МСб = 0 → НВ= МСб / f
∑ m С лев = 0 → НВ* f - R В* l + ∑ Fi * ( l В - в i ) = Н A* f – МСб = 0 → НВ= МСб / f
Н A = НВ= Н = МСб / f


 Определение усилий в арке
Определение усилий в арке
M ар к = Мкб - Нук Q ар к = Q б к cos θ - Hsin θ N ар к = - [ Q б к sin θ + Hcos θ ]
Пример 1 расчёта арки на неподвижную нагрузку

Пример 2 расчёта арки на неподвижную нагрузку

 Рациональное очертание оси ТША
Рациональное очертание оси ТША
Теорема: Пропорциональность вертикальных ординат у всех точек оси арки, отсчитываемых от опорной прямой АВ, соответствующим ординатам «балочной» эпюры Мб является необходимым и достаточным условием того, чтобы в трёхшарнирной арке при действии заданной вертикальной нагрузке изгибающий момент во всех сечения был равен нулю
Пусть ук= k* Мкб , тогда M ар к = Мкб- Н*ук= Мкб- Н* k* Мкб= Мкб (1 – Н * k )
так как Мкб= МСб ≠ 0 , следовательно (1 – Н * k ) = 0 при произвольном k = const
















 q
q

у
f
 А В
А В




















 х
х
ql /2 l а l в ql /2

L

Пусть ук=4 f х ( l -х)/ l 2 . Распор Н= МСб / f = q l 2 /(8 f). Тогда M ар к = Мкб- Н*ук=…=0
Л е к ц и я 11-14
РАСЧЁТ ПЕРЕМЕЩЕНИЙ
В ПЛОСКИХ СТЕРЖНЕВЫХ СИСТЕМАХ
 Обсуждаемые вопросы (план лекции)
Обсуждаемые вопросы (план лекции)
Пример 1 расчёта перемещений в раме

Пример 2 расчёта перемещений в раме

МАТРИЧНАЯ ФОРМА ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
Матричная азбука : Матрица – прямоугольная таблица чисел, имеющая m строк и n столбцов, которые называются размерами матрицы.
А = ║аij ║ - i = 1, 2, …, m ; j = 1, 2, …, n ;
Виды матриц : 1) квадратная матрица при m = n ;
Пример расчёта рамы в матричной форме

СТРОИТЕЛЬНАЯ МЕХАНИКА
РАСЧЁТ СТЕРЖНЕВЫХ СИСТЕМ
ОБЩИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Статически неопределимыми системами (СНС) называется системы, в которых уравнений статики недостаточно для определения всех реакций опорных связей и внутренних силовых факторов
Шарниров в жёсткие узлы

 | |||
 | |||

Примеры расчёта статической неопределимости
Пример №1 Пример №2



 Пример №3 Пример №4
Пример №3 Пример №4
МЕТОД СИЛ
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
При проведении расчёта МС исходная СНС приводится к статически определимой геометрически неизменяемой системе (путём устранения в ней лишних связей) с введением в ней сил и моментов, заменяющих устранённые связи.
РАСЧЁТ СНС НА ОСАДКУ ОПОР
От внешней нагрузки
1 способ: после определения реакций в лишних связях они прикладываются к основной системе наряду с внешней нагрузкой и обычным образом строятся (в СОС) эпюры М, Q , N .
2 способ: 1) строится эпюра изгибающих моментов на основе формулы

От температуры и смещения опор
1 способ: после определения реакций в лишних связях они прикладываются к основной системе наряду с внешней нагрузкой и обычным образом строятся (в СОС) эпюры М, Q , N .
2 способ: 1) строится эпюра изгибающих моментов на основе формулы
Грузовых членов уравнений
(М F ) · (М s )= … = Σ i ΔiF ;
4) правильность эпюры М - по равновесию упругих узлов;
5) правильность эпюры М - деформационная проверка !
(М) · (М s )= … =0;
6) правильность эпюры М, Q , N - статическая проверка всей системы или любой её отсечённой части
Пример 1 расчёта рамы методом сил


/
Пример 2 расчёта рамы методом сил

МАТРИЧНАЯ ФОРМА МЕТОДА СИЛ
Пример 1 расчёта неразрезной балки методом сил
 |  |

λ i ·М i -1 + 2·(λi+λ i +1 )·М i + λ i +1 ·М i +1 = -6·Е J 0 ·[а i ·ω i /( l i ·Е Ji )+ bi +1 ·ω i +1 /( l i +1 ·Е Ji +1 )]
Е J i = Е J 0 = Е J ; λ1 = l 1 = 4,5 м ; λ2 = l 2 = 6 м ; λ3= l 3 = 6 м
Левая опора – шарнирная : i =1 → 2·(λ1+λ2)·М1 + λ2·М2 = -6· [а1·ω1/ l 1 + b 2 ·ω2/ l 2 ] = -6· [А1 +В2]

2(4,5+6) ·М1 + 6·М2 = -6·(6,07 + 17,8) 21·М1 + 6·М2 = - 143,22
Правая опора – шарнирная : i =2 → λ2 ·М1+2·(λ2+λ3)·М2 = -6·[а2·ω2/ l 2 + b 3 ·ω3/ l 3 ] = -6· [А2 +В3]

6·М1 + (6+6)·М2 = -6·(18,8 + 13,8) 6·М1 + 12·М2 = -195,6
Решая СЛУ, получаем: М1= -4,89 т · м; М2 = - 6,93 т · м
Пример 2 расчёта неразрезной балки методом сил

УРАВНЕНИЕ ПЯТИ МОМЕНТОВ
Расчётная схема

Классификация арок
 |  |  |

 Двухшанирная арка
Двухшанирная арка

 n = 1
n = 1
Бесшанирная арка Одношанирная арка 

n = 
 3 n = 2
3 n = 2
Особенности расчёта арок
При расчёте перемещений приходится учитывать влияние всех силовых факторов ( M , Q , N ) – в отличие от рам, арки не являются «примущественно» изгибаемыми системами. Следовательно, при расчёте методом сил количество эпюр усилий утраивается и
δiJ = δJi = ( MJ )* ( Mi ) + ( QJ )* ( Qi ) + ( NJ )* ( Ni )
ΔiF = (MF) * (Mi) + (QF) * (Qi) + (NF) * (Ni)
2. Криволинейность эпюр M , Q , N (вследствие криволинейности оси арки) не позволяет использовать правило Верещагина для «силовых» участков арки, приходится вводить значительное число дополнительных расчётных участков , в пределах которых ( приближённо ) применимо правило Верещагина – это обстоятельство приводит к существенному увеличению объёмов аналитических расчётов.
Виды осей арок
 |  |  |
Кольцевые (полукольцевые) Полуэллиптические Стрельчатые
Достоинства арок:
1. экономичность при перекрытии больших пролетов;
2. высокие архитектурные качества;
3.
Недостатки арок:
1. сложность аналитического расчёта;
2. высокая «чувствительность» к осадкам опор;
3.
Назначение арок:
1. складские помещения, ангары, …;
2. спортивные арены, тренировочные залы, ….;
3.
 Расчёт двухшарнирной арки с затяжкой
Расчёт двухшарнирной арки с затяжкой
 | |||
 | |||




 у
у


 φ
φ

 у = f (х)
у = f (х)
у







 х
х


 х Х=Нз
х Х=Нз


Mx = - y ; Nx = - cos φ; Qx = - sin φ; MxF = Mx б ; NxF = Qx б cos φ; QxF = - Qx б sin φ;
Х=Нз = - Δ F /(δа+ δз) при δз = l з /(ЕАз)
МЕТОД ПЕРЕМЕЩЕНИЙ
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
При проведении расчёта МП из исходной СНС образуется путём введения в ней «плавающих» заделок в упругие узлы и линейных связей по направлениям возможных перемещений основная (расчётная) система.
n = n СКН = n у + n л
где: n у – число упругий узлов (УУ) в исходной СНС ; n л – число возможных линейных перемещений УУ
Основная система МП
 |  |



 F 1 Z 1 F 1 Z 2 Z 3
F 1 Z 1 F 1 Z 2 Z 3
 | |||
 | |||

 F 2 F 2
F 2 F 2


 1
1
 | |||
 | |||








Исходная СНС Основная система МП
Грузовых членов уравнений
(М F ) · (М s )= … = Σ i RiF ;
4) правильности решения СЛУ;
5) правильность эпюры М - по равновесию упругих узлов;
6)  правильность эпюры М - деформационная проверка !
правильность эпюры М - деформационная проверка !
(М) · (М s ос мс )= … =0;
М s ос мс - где суммарно единичная эпюра в любой основной системе метода сил;
7) правильность эпюры М, Q , N - статическая проверка всей системы или любой её отсечённой части
ПРИМЕР 1 РАСЧЁТА СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ РАМЫ МЕТОДОМ ПЕРЕМЕЩЕНИЙ

СМЕШАННЫЙ МЕТОД РАСЧЁТА СНС
ПРИМЕР 1 РАСЧЁТА СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ РАМЫ СМЕШАННЫМ МЕТОДОМ

ПРИБЛИЖЁННЫЕ МЕТОДЫ РАСЧЁТА
ПОНЯТИЕ О
ДИНАМИКЕ СООРУЖЕНИЙ
ПОНЯТИЕ О
УСТОЙЧИВОСТИ СООРУЖЕНИЙ
ПОНЯТИЕ О
СТРОИТЕЛЬНАЯ МЕХАНИКА
РАСЧЁТ СТЕРЖНЕВЫХ СИСТЕМ
Раздел 1 – расчет статически определимых систем
Последнее изменение этой страницы: 2019-05-08; Просмотров: 331; Нарушение авторского права страницы