Дисперсия случайной величины, имеющей распределение Пуассона.
Дисперсией случайной величины Х называют математической ожидание квадрата отклонения случайной величины от ее математического ожидания:


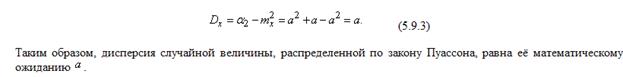
Это свойство распределения Пуассона часто применяют на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики - математическое ожидание и дисперсию - случайной величины. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении; резкое различие этих характеристик, напротив, свидетельствует против подобной гипотезы.
1.Определение случайной величины и связанных с ней понятий: распределения и функции распределения. Случайной величиной называется функция 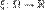 , измеримая относительно
, измеримая относительно 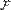 и борелевскойσ-алгебры на
и борелевскойσ-алгебры на  .
.
Случайную величину можно определить и другим эквивалентным способом. Функция 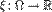 называется случайной величиной, если для любых вещественных чисел
называется случайной величиной, если для любых вещественных чисел  и
и 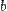 множество событий
множество событий 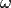 , таких что
, таких что 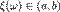 , принадлежит
, принадлежит  .
.
Пусть дано вероятностноепространство 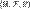 , и на нём определена случайнаявеличина
, и на нём определена случайнаявеличина  с распределением
с распределением 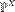 . Тогда функцией распределения случайной величины
. Тогда функцией распределения случайной величины 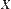 называется функция
называется функция 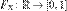 , задаваемая формулой:
, задаваемая формулой:
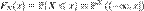 .
.
То есть функцией распределения (вероятностей) случайной величины  называют функцию
называют функцию 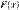 , значение которой в точке
, значение которой в точке  равно вероятности события
равно вероятности события 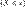 , то есть события, состоящего только из тех элементарных исходов, для которых
, то есть события, состоящего только из тех элементарных исходов, для которых 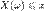 .
.
2.Дискретные случайные величины, законы распределения, примеры (распределение Бернулли, биномиальное распределение, распределение Пуассона).
Если случайная величина  дискретна, то есть её распределение однозначно задаётся функциейвероятности
дискретна, то есть её распределение однозначно задаётся функциейвероятности
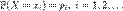 ,
,
то функция распределения  этой случайной величины кусочно-постоянна и может быть записана как:
этой случайной величины кусочно-постоянна и может быть записана как:
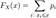 .
.
Эта функция непрерывна во всех точках 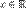 , таких что
, таких что 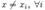 , и имеет разрыв первого рода в точках
, и имеет разрыв первого рода в точках 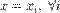 .
.
Закон распределения вероятностей р(m)определяется формулой Бернулли:
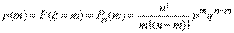 .Закон распределения вероятностей по формуле Бернулли часто называют биномиальным, так как Pn(m) представляет собой m-й член разложения бинома
.Закон распределения вероятностей по формуле Бернулли часто называют биномиальным, так как Pn(m) представляет собой m-й член разложения бинома 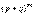 .
.
Пусть случайная величина 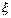 может принимать любое целое неотрицательное значение, причем
может принимать любое целое неотрицательное значение, причем
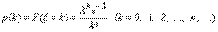 . Распределение Пуассона . Распределение Пуассона 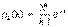 , k =0, 1, 2,..
3. Математическое ожидание дискретной случайной величины и его свойства.
Пусть , k =0, 1, 2,..
3. Математическое ожидание дискретной случайной величины и его свойства.
Пусть 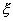 - дискретная случайная величина с заданным законом распределения вероятностей - дискретная случайная величина с заданным законом распределения вероятностей 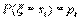 Математическим ожиданием Математическим ожиданием 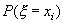 дискретной случайной величины дискретной случайной величины 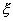 называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е. *
1°. Математическое ожидание постоянной С равно этой постоянной. Доказательство. Постоянную C можно рассматривать как случайную величину называется сумма парных произведений всех возможных значений случайной величины на соответствующие им вероятности, т.е. *
1°. Математическое ожидание постоянной С равно этой постоянной. Доказательство. Постоянную C можно рассматривать как случайную величину 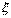 , которая может принимать только одно значение C c вероятностью равной единице. Поэтому , которая может принимать только одно значение C c вероятностью равной единице. Поэтому 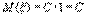 2°. Постоянный множитель можно выносить за знак математического ожидания, т.е. 2°. Постоянный множитель можно выносить за знак математического ожидания, т.е.
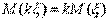 Доказательство. Используя соотношение, имеем Доказательство. Используя соотношение, имеем
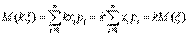 3°. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин:
3°. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин:
4°. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин **:
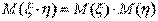 4. Математическое ожидание дискретной случайной величины, имеющей распределение Бернулли, биномиальное распределение, распределение Пуассона. Биномиальное распределение (распределение Бернулли)
Возникает в тех случаях, когда ставится вопрос: сколько раз происходит некоторое событие в серии из определенного числа независимых наблюдений (опытов), выполняемых в одинаковых условиях. P(X= k) =
4. Математическое ожидание дискретной случайной величины, имеющей распределение Бернулли, биномиальное распределение, распределение Пуассона. Биномиальное распределение (распределение Бернулли)
Возникает в тех случаях, когда ставится вопрос: сколько раз происходит некоторое событие в серии из определенного числа независимых наблюдений (опытов), выполняемых в одинаковых условиях. P(X= k) = 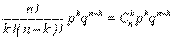 , где k=0,1,…n
Формулу называют формулой Бернулли. При большом числе испытаний биномиальное распределение стремиться к нормальному.Распределение Пуассона Играет важную роль в ряде вопросов физики, теории связи, теории надежности,теории массового обслуживания и т.д. P(Z=k) = , где k=0,1,…n
Формулу называют формулой Бернулли. При большом числе испытаний биномиальное распределение стремиться к нормальному.Распределение Пуассона Играет важную роль в ряде вопросов физики, теории связи, теории надежности,теории массового обслуживания и т.д. P(Z=k) = 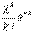 5. Дисперсия и среднеквадратическое отклонение дискретной случайной величины, свойства дисперсии.Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания:D(X) = (x1 - M(X))2p1 + (x2 - M(X))2p2 + ... + (xn- M(X))2pn = x21p1 + x22p2 + ... + x2npn - [M(X)]2. Свойства дисперсии. 1) Дисперсия постоянной величины равна нулю: D(С) = 0 2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С2 · D(Х) 3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х1 ± Х2 ± ... ± Хn) = D(Х1) + D(Х2) + ... + D(Хn) Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное продолжение 5. отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии: σ(X) = √D(X).
6. Определение независимых случайных величин. Математическое ожидание произведения и дисперсия суммы независимых случайных величин..Две случайные величины называютсянезависимыми, если законраспределения одной из них не зависит от того, какие значения приняла другая. В противном случае случайные величины зависимы.Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий плюс корреляционный момент:
5. Дисперсия и среднеквадратическое отклонение дискретной случайной величины, свойства дисперсии.Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания:D(X) = (x1 - M(X))2p1 + (x2 - M(X))2p2 + ... + (xn- M(X))2pn = x21p1 + x22p2 + ... + x2npn - [M(X)]2. Свойства дисперсии. 1) Дисперсия постоянной величины равна нулю: D(С) = 0 2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С2 · D(Х) 3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х1 ± Х2 ± ... ± Хn) = D(Х1) + D(Х2) + ... + D(Хn) Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное продолжение 5. отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии: σ(X) = √D(X).
6. Определение независимых случайных величин. Математическое ожидание произведения и дисперсия суммы независимых случайных величин..Две случайные величины называютсянезависимыми, если законраспределения одной из них не зависит от того, какие значения приняла другая. В противном случае случайные величины зависимы.Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий плюс корреляционный момент:  . Дисперсия суммы двух случайных величин равна сумме их дисперсий плюс удвоенный корреляционный момент: . Дисперсия суммы двух случайных величин равна сумме их дисперсий плюс удвоенный корреляционный момент: 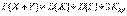
|
|
|
1.16.Полная группа событий, априорная и апостериорная вероятность.теорема Байеса.
По́лнойгру́ппойсобы́тий в теории вероятностей называется система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно из них.
Пусть 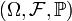 есть вероятностное пространство. Любое разбиение множества
есть вероятностное пространство. Любое разбиение множества  элементами сигма-алгебры
элементами сигма-алгебры 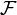 называется полной группой событий.
называется полной группой событий.
Теорема Байеса- формула, позволяющая вычислять апостериорные вероятности событий (или гипотез) через априорные вероятности. Пусть 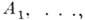 - полная группа несовместимых событий
- полная группа несовместимых событий 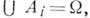 : при
: при 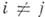 . Тогда апостериорная вероятность
. Тогда апостериорная вероятность 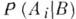 события
события 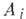 при условии, что произошло событие В
при условии, что произошло событие В 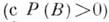 , может быть найдена по формуле Бейеса:
, может быть найдена по формуле Бейеса: 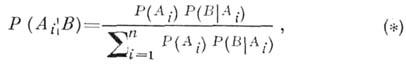
Где 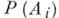 - априорная вероятность события
- априорная вероятность события 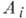 ,
, 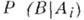 - условная вероятность события Впри условии, что произошло событие
- условная вероятность события Впри условии, что произошло событие 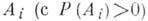 .
.
АПОСТЕРИОРНАЯ ВЕРОЯТНОСТЬ какого-либо события - условная вероятность события при нек-ром условии, рассматриваемая в противоположность его безусловной или априорной вероятности.
1.17События называются независимыми в совокупности, если каждое из них и любое произведение остальных (включающее либо все остальные события, либо часть из них) есть события независимые.События, независимые в совокупности, попарно независимы между собой; обратное утверждение неверно.
Теорема умножения произвольных событий. Вероятность произведения двух произвольных событий равна произведению вероятности одного из них на условную вероятность другого, в предположении, что первое имеет место, т.е. P(AB) = P(A)P(B|A) = P(B)P(A|B).
Следствие. Для любых двух событий А и В справедливо равенство P(A)P(B|A) = P(B)P(A|B).
Теорема умножения произвольных событий допускает обобщение на случай нескольких событий.
Теорема умножения независимых событий. Вероятность совместного появления двух независимых событий А и В равна произведению вероятностей этих событий: P(AB) = P(A)P(B).
Теорема умножения независимых в совокупности событий. Вероятность произведения конечного числа независимых в совокупности событий равна произведению вероятностей этих событий:
P(A1 x A2 x...x An) = P(A1) x P(A2) x...x P(An).
Формула полной вероятности. Если Н1….Нп-полная группа попарно несовместных событий(т.е сумма этих событий есть достоверное событие и никакие два из них не могут произойти одновременно) то вероятность любого события А может быть вычислена с помощью формулы полной вероятности :
Р(А)=Р(Н1)Р(А│Н1)+…+Р(Нп)Р(А│Нп).
События Н1….Нп называются при этом гипотезами ,а вероятности Р(Н1)…Р(Нп) -априорными вероятностями гипотез.

