
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Равновесие нити на поверхности
Задача 1. Невесомая нить находится в равновесии на шероховатой цилиндрической поверхности (рис 2.5). Коэффициент трения равен k=0, 1, угол охвата φ =1200. Натяжение нити на конце А равно ТА = 10 Н. Определить натяжение нити на конце В.
Составим дифференциальное равновесие нити в проекциях на оси естественного трехгранника, связанного с поверхностью (1.21).
Из последнего уравнения находим υ = 0, т.е. угол геодезического отклонения равен нулю, нить располагается по горизонтальной кривой и ρ = R.
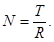 Сила трения согласно закону Амонтона Сила трения согласно закону Амонтона  Подставляя в первое уравнение, получим: Подставляя в первое уравнение, получим:
Интегрируя, находим
Окончательно получаем натяжение
Задача 2.
φ В = 1800 и φ С = 600.
Решение. Составим дифференциальные уравнения равновесия нити в проекции на оси естественного трехгранника (1.20).
Решая первое уравнение, учитывая, что ds = Rdφ , dT = - qcosφ · Rdφ , Интегрируя, находим Т = - qRsinφ + C 1 Учитывая, что при φ = 0 Т = ТА, находим С1 = ТА. Тогда натяжение в любой точке нити равно Т = ТА – qRsinφ . Натяжение в т. В ТВ = ТА – qRsin 1800 = TA Натяжение в т. С ТС = ТА – qRsin 600 = 0, 1 – 0, 2·0, 1·0, 866 = 0, 083 Н.
Задача 3.
Определить коэффициент трения поверхности.
Составим уравнения равновесия нити на шероховатой поверхности в проекциях на оси естественного трехгранника, связанного с поверхностью, согласно (2.21)
Из второго уравнения с учетом закона Амонтона находим
Из полученного неравенства следует, что Как как имеем k ≥ tg450, т.е. k ≥ 1.
Задача 4. Однородная нерастяжимая нить, весом которой можно пренебречь, огибает шероховатую поверхность цилиндра. Коэффициент трения нити на поверхности k=0, 3. Натяжение конца А нити равно Решение. Рассмотрим равновесие нити на шероховатой поверхности шкива (рис. 2.8). Начало отсчета дуговой координаты совместим с точкой А. За положительное направление отсчета дуговой координаты примем направление против хода часовой стрелки. Выберем произвольно точку М и покажем действующие на нить силы, отнесенные к единице длины.
Рис. 2.8
Касательную ось Составим дифференциальные уравнения равновесия нити в проекциях на оси естественного трехгранника. Нить расположена по геодезической кривой цилиндра, поэтому угол геодезического отклонения
Выразим из второго уравнения системы нормальное давление: и выразив силу трения подставим ее выражение в первое уравнение системы:
Заменим ds=Rdφ и получим:
Умножая на Rdφ и деля на Т, получим: Проинтегрируем неравенство:
Для определения постоянной интегрирования С1, рассмотрим граничные условия в точке А:
Подставляя значение С1 в неравенство (2.36), учитывая, что разность логарифмов равна логарифму соотношения и потенцируя полученное неравенство, находим натяжение в любой точке нити на участке АВ:
Найдем натяжение в точке В, для которой
Подставив численные значения, получим условие для натяжения в точке В:
Задача 5.
Выразим натяжение ТА точки А нити: Подставив численное значение веса груза 1, получим натяжение ТА:
2. Рассмотрим равновесие участка АВ. Примем точку А за начало декартовой системы координат и направим ось Ах вертикально вверх.
Рис. 2.11 Натяжение невесомой прямолинейной нити одинаково в каждой точке нити, следовательно
Получим натяжение в точке В нити: 3. Рассмотрим равновесие нити шероховатой поверхности конуса 2 (рис. 2.12). Начало отсчета дуговой координаты совместим с точкой В. За положительное направление отсчета дуговой координаты примем направление против хода часовой стрелки.
Рис. 2.12
Выберем произвольно точку М и покажем действующие на нить силы, отнесенные к единице длины. Касательную ось Радиус кривизны нити ρ равен радиусу рассматриваемой окружности конуса R. Запишем условия равновесия нити на круговом конусе: 1). При отсутствии активных сил (Р=0) для равновесия нити на шероховатой поверхности, необходимо, чтобы коэффициент трения нити был не меньше угла геодезического отклонения В нашем случае это условие выполняется 2). Для натяжения точек нити должно соблюдаться условие [5]:
где Вычислим Учтем, что ρ =R и запишем условие равновесия нити на круговом конусе:
Подставим численные значения
4. Рассмотрим равновесие участка CD. Примем точку C за начало декартовой системы координат и направим ось Cх горизонтально влево.
Рис. 2.13
Так как натяжение невесомой прямолинейной нити одинаково в каждой точке нити, то
Учитывая условие (7), получим натяжение в точке В нити:
Таким образом, натяжение в точке D меньше, чем натяжение в точке А. 5. Рассмотрим равновесие точки D нити и груза 3.
Рис.2.14 Примем точку D за начало декартовой системы координат и направим ось Dх вдоль плоскости влево, а Dу – вверх. Силу трения Запишем уравнения равновесия груза в проекциях на оси координат:
и дополнительное условие равновесия груза Fтр≤ fN. (2.45) Выразим из второго уравнения (2.44) нормальное давление плоскости N
и подставим его в ρ =R, силу трения груза о плоскость полученным неравенством и выразим условие для веса груза:
Подставив численное значение f=0, 4 и условие для натяжения в точке D (2.43), найдем вес груза 3, необходимый для уравновешивания системы:
Задача 6.
Решение. Разобьем длину нити на участки: груз 1, свободный участок АВ, участок ВС на гладкой поверхности цилиндра. Примем, что натяжение в точке С нити больше, чем натяжение в точке А, ТС > ТА. 1. Рассмотрим равновесие нити гладкой поверхности цилиндра 2 (рис. 2.16). Начало отсчета дуговой координаты совместим с точкой С. Выберем произвольно точку М и покажем действующие на нить силы, отнесенные к единице длины. Касательную ось
Рис. 4
Составим дифференциальные уравнения равновесия нити в проекциях на оси естественного трехгранника. Нить расположена по геодезической кривой цилиндра, поэтому угол геодезического отклонения
Рассмотрим первое уравнение системы, заменив ds=Rdφ:
Проинтегрируем равенство
Для определения постоянной интегрирования С2, рассмотрим граничные условия в точке С:
Подставляя значение С2 в равенство, находим натяжение в любой точке нити на участке ВС:
Получим условие для натяжения в точке В для которой:
2. Рассмотрим равновесие отрезка АВ нити (рис.2.17). Примем точку В за начало декартовой системы координат и направим ось Вх по нити вниз. Покажем силы, действующие на произвольную точку М: натяжения на концах участка и вес единицы длины нити.
Рис.2.17.
Составим дифференциальное уравнение равновесия нити, проецируя вес на ось координат Вх: Так как нить прямолинейна, то есть ds=dx, то дифференциальное уравнение принимает вид:
Для определения постоянной интегрирования С3 рассмотрим граничные условия в точке В: Подставляя значение С1 в равенство, получим натяжение в любой точке нити на участке АВ:
Определим натяжение точки А нити, в которой
Учитывая условие для Тв, получим натяжение в точке A нити:
Примем точку А за начало декартовой системы координат и направим ось Ах вниз вдоль плоскости, а Ау – перпендикулярно плоскости, вверх. Силу трения Запишем уравнения равновесия груза в проекциях на оси координат:
и дополнительное условие равновесия груза Fтр≤ fN. (2.55) Выразим из уравнения (2.54) нормальное давление плоскости N
и подставим его в неравенство (2.55): Заменим в уравнении (2.53) силу трения груза о плоскость полученным неравенством и выразим условие для натяжения нити:
Найдем натяжение точки А нити, подставив числовые значения:
Подставим в неравенство значение натяжения ТА:
Определим натяжение в точке С: Задача 7. Однородная нерастяжимая нить, весом q, Н/м, огибает шероховатую поверхность цилиндра, перпендикулярно образующим (рис. 2.19). Радиус цилиндра равен R, м. Коэффициент трения нити о поверхность k. Определить, каким должно быть натяжение в т. В нити, что бы нить находилась в равновесии.
Рассмотрим равновесие нити на шероховатой цилиндрической поверхности шкива. Начало отсчета дуговой координаты совместим с точкой К, считая, что натяжение нити в точке больше, чем в точке В. Нить расположена по геодезической кривой цилиндрической поверхности, поэтому угол геодезического отклонения θ =0, а радиус кривизны нити равен радиусу шкива ρ =r. Начало естественного трехгранника совместим с точкой М нити и направим касательную ось Составим дифференциальные уравнения равновесия нити в проекциях на оси естественного трехгранника
Из второго уравнения системы выразим N:
Тогда сила трения будет определятся неравенством:
Подставим выражение силы трения в первое уравнение системы (2.58) и учтем, что ds = rdφ . Получим неравенство:
Перепишем неравенство, умножая почленно на rdφ :
Умножая полученное неравенство почленно на ekφ , получим:
Выражение, стоящее в левой части неравенства, представляет собой полный дифференциал произведения (е kφ T), в чем можно убедиться непосредственным дифференцированием.
Запишем неравенство (2.21) в виде:
И проинтегрируем, учитывая, что:
После интегрирования и приведения подобных получаем:
Для определения постоянной интегрирования С1 составим граничные условия в точке К: при φ = φ К =0 Т=ТК. Подставляя граничные условия в неравенство (2.60), получим:
Откуда находим:
Подставляя значение С1 в неравенство (2.60), имеем
Разделив почленно на
Найдем натяжение нити в точке L, положив в неравенстве (2.23) значение
Положив в неравенстве (2.23)
Так как нить охватывает шкив снизу, то возможно нарушение контакта нити с поверхностью. Самой опасной точкой в этом смысле является точка L. Условие наличия контакта нити со шкивом в точке L имеет вид NL≥ 0. Нормальное давление N определим из второго уравнения системы (2.20):
Подставим в равенство (2.26) Т=Т L;
Отсюда находим, что при этом должно выполнятся условие: Т L ≥ qr. (2.65) Значит, выбранное согласно условию (2.62) значение натяжения Т L должно одновременно удовлетворять условию (2.65). 3. Задачи для самостоятельной работы |
Последнее изменение этой страницы: 2019-10-04; Просмотров: 194; Нарушение авторского права страницы