Оптимальный по быстродействию разворот в пространстве

Рассмотрим задачу переориентации летательного аппарата в пространстве за минимальное время. В качестве уравнений движения примем уравнения Эйлера

	(13.25)
.

Здесь , ,  - проекции угловой скорости на связанные оси; , ,  - компоненты управляющего момента вдоль этих осей; , , , - моменты инерции по связанным осям . На компоненты управляющего момента накладываются ограничения

, , ,

(13.26)

Будем полагать, что разворот ЛА происходит с угловой скоростью  относительно некоторой неподвижной в пространстве оси. Данное предположение не нарушает общности рассмотрения задачи, так как любой разворот твердого тела в пространстве можно представить как разворот его относительно неподвижной оси в пространстве, называемой осью Эйлера.

Обозначая через  направляющие косинусы этой оси в связанной системе координат, можно записать

, , .

Если теперь через  обозначить угол разворота относительно неподвижной оси, то ее математическую модель можно представить следующем виде

 ,

,	(13.27)
,
,

что эквивалентно двум дифференциальным уравнениям

,

(13.28)

при двух конечных связях

	(13.29)
,

где

; ;	(13.30)
; ; .

Требуется найти такое управление , , , которое с учетом условий (13.26) и (13.29) осуществит перевод системы (13.28) из начального состояния 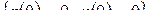 в конечное  за минимальное время.

Итак, критерий оптимальности имеет вид

,

(13.31)

причем свободно. Выявим с помощью необходимых условий оптимальности (13.22) структуру оптимального управления. Составим гамильтониан для данной задачи

(13.32)

Если через обозначить вектор с компонентами и , то матрица , которая согласно (13.29) запишется как

,

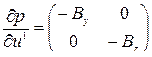будет иметь обратную , что означает возможность осуществления движения вдоль границы .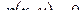

Уравнения для компонент ,  согласно (13.22) имеют вид

;	(13.33)
.

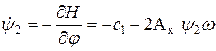Можно показать, что при неизменном знаке  функция  изменяет свой знак не более одного раза.

В соответствии с (13.22) оптимальное управление обращает в минимум гамильтониан (13.32) при ограничениях (13.26) и (13.29). По сути дела, имеем задачу минимизации линейной по управлению формы (13.32) на плоскости

(13.34)

при наличии ограничений

, , .

(13.35)

Задача имеет наглядную геометрическую интерпретацию. В системе координат , , , т.е. в связанной системе координат, плоскость (13.34) и параллелепипед (13.35) при пересечении в общем случае образуют жестко связанный с ЛА многоугольник допустимых элементов управления.

В силу линейности гамильтониана от управления минимум  достигается на границе этого многоугольника, т.е. в любой момент времени одна из компонент момента управления обязательно принимает свое максимальное значение, две другие определяются однозначно таким образом, чтобы результирующий момент управления оказался на границе многоугольника.

Поскольку по условию задачи в начальный и конечный моменты времени , то согласно (13.29) векторы момента управления для этих времен лежат на одной и той же хорде, проходящей через начало координат. Однако направлены они в противоположные стороны, что физически означает в одном случае разгон, а в другом - торможение летательного аппарата.

В силу того, что компонента  может менять знак лишь один раз, переключение момента управления с режима разгона на режим торможения также возможно только один раз. Учитывая сказанное, нетрудно построить годограф, описываемый концом вектора момента оптимального управления.

Итак, структура оптимального управления определена с точностью до знания момента переключения  и момента окончания процесса управления . Интегрируя уравнения движения (13.28) при найденном управлении с момента  до момента , можно получить, систему из двух уравнений

относительно неизвестных  и .

 

Упражнение 1. Построить для рассмотренной задачи многоугольник допустимых моментов управления в общем случае. Показать годограф, описываемый концом вектора момента оптимального управления. Какие возможны частные случаи?

Упражнение 2. Решить задачу об оптимальной по быстродействию переориентации летательного аппарата в случае полной симметрии, т.е. при условии .

Упражнение 3. Найти оптимальное управление в задаче управления спуска, рассмотренной ранее, при движении вдоль изотермического ограничения вида , полагая, что плотность атмосферы изменяется по экспоненциальному закону , где 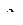 - плотность у поверхности Земли;  - высота; 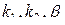- константы.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться: