Раздел 1. Классическая вероятностная схема

Раздел 1. Классическая вероятностная схема

Основные формулы комбинаторики

В данном разделе мы займемся подсчетом числа «шансов». О числе шансов говорят, когда возможно несколько различных результатов какого-либо действия (извлечение карты из колоды, подбрасывание кубика или монетки, двух кубиков и т.д.). Число шансов — это число таких возможных результатов, или, иначе говоря, число способов проделать это действие.

Теорема о перемножении шансов

Теорема 1. Пусть имеется, k групп элементов, причем i-я группа содержит n_i элементов, 1< = i < = k. Выберем из каждой группы по одному элементу. Тогда общее число N способов, которыми можно произвести такой выбор, равняется

Замечание 1. В теореме 1 считается, что даже если все элементы в i-й группе неразличимы, выбрать один из них можно n_i способами.

Замечание 2. Результат выбора, описанного в теореме 1, представим в виде набора (а₁, а ₂, …, а _k) в котором а _i — выбранный из i-й группы элемент. Тогда общее число различных наборов (а₁, а ₂, …, а _k) также равняется

Доказательство теоремы 1.

 

Занумеруем элементы i -ой группы числами от 1 до n_i. Элемент из первой группы можно выбрать n ₁ способами. Если мы выбрали элемент j, 1< = i < = n ₁, то выбрать элемент из второй группы мы можем n ₂ способами. Получаем, что с первым элементом j возможно составить n ₂ пар ( j, l ), где 1< = l < = n ₂.

Но столько же пар можно составить и с любым другим элементом первой группы. Тогда всего пар, в которых первый элемент выбран из первой группы, а второй — из второй, существует ровно

Иначе говоря, есть  способов выбрать по одному элементу из первых двух групп. Возьмем одну такую пару ( j, l ). Заметим, что элемент из третьей группы можно выбрать n ₃ способами, то есть возможно составить ровно n ₃ троек ( j, l, m ), добавляя к данной паре ( j, l ) любой из n ₃ элементов третьей группы.

Но столько же троек можно составить и с любой другой парой ( j, l ). Тогда всего троек, в которых первый элемент выбран из первой группы, второй — из второй, а третий — из третьей, существует ровно .

Продолжая рассуждения, методом математической индукции заключаем справедливость утверждения теоремы.

Урны и шарики

Есть урна, (то есть ящик), содержащая n занумерованных объектов, которые мы без ограничения общности будем считать шариками. Мы выбираем из этой урны k шариков. Нас интересует, сколькими способами можно выбрать k шариков из n, или сколько различных результатов (то есть наборов, состоящих из k шариков) получится.

На этот вопрос нельзя дать однозначный ответ, пока мы не определимся

· с тем, как организован выбор (скажем, можно ли шарики возвращать в урну), и

· с тем, что понимается под различными результатами выбора.

Рассмотрим следующие возможные схемы выбора:

1. Выбор с возвращением: каждый выбранный шарик возвращается в урну, то есть каждый из k шариков выбирается из полной урны. В полученном наборе, состоящем из k номеров шариков, могут встречаться одни и те же номера (выборка с повторениями).

2. Выбор без возвращения: выбранные шарики в урну не возвращаются, и в полученном наборе не могут встречаться одни и те же номера (выборка без повторений).

И в том, и в другом случае результатом выбора является набор из k номеров шариков. Удобно считать, что шарики всегда выбираются последовательно, по одному (с возвращением или без).

Условимся, какие результаты мы будем считать различными.

Есть ровно две возможности.

1. Выбор с учетом порядка: два набора номеров шариков считаются различными, если они отличаются составом или порядком номеров. Так, при выборе трех шариков из урны, содержащей 5 шариков, наборы (1, 2, 5), (2, 5, 1) (4, 4, 5) различны, если производится выбор с учетом порядка.

2. Выбор без учета порядка: два набора номеров шариков считаются различными, если они отличаются составом. Наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми. Так, в примере выше первые два набора (1, 2, 5), (2, 5, 1) есть один и тот же результат выбора, а набор (4, 4, 5) — другой результат выбора.

Подсчитаем теперь, сколько же возможно различных результатов при каждой из четырех схем (выбор с возвращением и без, и в каждом из этих случаев учитываем ли мы порядок или нет).

Основные понятия элементарной теории вероятностей

Пример 7.

Из урны, в которой n ₁ белых и n - n ₁ чёрных шаров, наудачу, без возвращения вынимают k шаров, k < n. Термин «наудачу» означает, что появление любого набора из k шаров равно возможно. Найти вероятность того, что будет выбрано ровно k ₁ белых и k - k ₁ чёрных шаров.

Заметим, что при k ₁ > n ₁ или k - k ₁ > n - n ₁ искомая вероятность равна 0, так как соответствующее событие невозможно. Пусть k ₁ < n ₁ и k - k ₁ < n - n ₁. Результатом эксперимента является набор из k шаров. При этом можно не учитывать или учитывать порядок следования шаров.

1. Выбор без учета порядка. Общее число элементарных исходов есть число k –элементных подмножеств множества, состоящего из n элементов, то есть  (по теореме 3).

Обозначим через A событие, вероятность которого требуется найти. Событию A благоприятствует появление любого набора, содержащего k ₁ белых шаров и k - k ₁ черных.

Число благоприятных исходов равно произведению (по теореме 1) числа способов выбрать k ₁ белых шаров из n ₁ и числа способов выбрать k - k ₁ черных шаров из n - n ₁:

Вероятность события A равна:

2. Выбор с учетом порядка. Общее число элементарных исходов есть число способов разместить n элементов на k местах  (по теореме 2).

При подсчете числа благоприятных исходов нужно учесть, как число способов выбрать нужное число шаров, так и число способов расположить эти шары среди k. Можно, скажем, посчитать число способов выбрать k ₁ мест среди k (равное 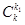), затем число способов разместить на этих k ₁ местах n ₁ белых шаров (равное  — не забывайте про учет порядка! ), и затем число способов разместить на оставшихся k - k ₁ местах n - n ₁ черных шаров (равное ). Перемножив эти числа, получим:

В рассмотренной задаче мы сопоставили каждому набору из k ₁ белых и k - k ₁черных шаров вероятность получить этот набор при выборе k шаров из урны, содержащей n ₁белых и n - n ₁черных шаров:

Определение 8. Соответствие или следующий набор вероятностей

Называется гипергеометрическим распределением.

Что это такое

Рассмотрим какую-нибудь область Ω в R^m , (на прямой, на плоскости, в пространстве). Предположим, что «мера» Ω (длина, площадь, объем, соответственно) конечна. Пусть случайный эксперимент состоит в том, что мы наудачу бросаем в эту область точку а. Термин «наудачу» здесь означает, что вероятность попадания точки в любую часть А Í Ω не зависит от формы или расположения А внутри Ω , а зависит лишь от «меры» области.

Определение 9. Эксперимент удовлетворяет условиям «геометрического определения вероятности», если его исходы можно изобразить точками некоторой области Ω в R^m так, что вероятность попадания точки в любую А Í Ω не зависит от формы или расположения А внутри Ω , а зависит лишь от меры области А (и, следовательно, пропорциональна этой мере):

«Мерой» мы пока будем называть длину, площадь, объем и т.д.

Если для точки, брошенной в область Ω , выполнены условия геометрического определения вероятности, то говорят, что точка равномерно распределена в области Ω.

Пример 8. Точка наудачу бросается на отрезок [0, 1]. Вероятность точке попасть в точку {0, 5} равна нулю, так как мера множества, состоящего из одной точки («длина точки»), есть 0. Вместе с тем попадание в точку {0, 5} не является невозможным событием — это один из элементарных исходов эксперимента.

Задача о встрече

Пример 9. Два лица Х и У условились встретиться в определенном месте между двумя и тремя часами дня. Пришедший первым ждет другого в течении 10 минут, после чего уходит. Чему равна вероятность встречи этих лиц, если каждый из них может прийти в любое время в течение указанного часа независимо от другого?

Будем считать интервал с 14 до 15 часов дня отрезком [0, 1] длиной 1 час. Пусть ξ («кси») и η («эта») — моменты прихода Х и У (точки отрезка [0, 1]).Все возможные результаты эксперимента — множество точек квадрата со стороной 1:

Ω = {( ξ , η ): 0 £ ξ £ 1 0 £ η £ 1 }=[0, 1]x[0, 1]

Можно считать, что эксперимент сводится к бросанию точки наудачу в квадрат. При этом благоприятными исходами являются точки множества A = {( ξ , η ): │ ξ - η │ £ 1/6 } (10 минут = 1/6 часа). То есть попадание в множество A наудачу брошенной в квадрат точки означает, что Х и У встретятся.

Тогда вероятность встреч и равна

Задача Бюффона

Пример 10. На плоскости начерчены параллельные прямые, находящиеся друг от друга на расстоянии 2 a. На плоскость наудачу брошена игла длины 2 l < 2 a. Какова вероятность того, что игла пересечет одну из прямых?

Поймем, что означает здесь «наудачу брошена игла». Возможные положения иглы (отрезка) на плоскости полностью определяются положением середины иглы и углом поворота иглы относительно какого-либо направления. Причем две эти переменные (положение центра и угол поворота) меняются независимо друг от друга. Обозначим через х Î [0, a ] расстояние от середины иглы до ближайшей прямой, а φ Î [0, π ] —

угол между каким-то направлением прямых и иглой. Множество возможных положений иглы целиком определяется выбором наудачу точки из прямоугольника Ω = [0, π ] x [0, a ]. Игла пересекает ближайшую прямую, если координаты выбранной наудачу точки удовлетворяют неравенству: х £ . l sin φ

Площадь области А Í Ω , точки которой удовлетворяют такому неравенству, равна

И так как μ (Ω ) = a π , то искомая вероятность равна

Парадокс Бертрана

Пример 11 ( Josef Bertrand, “Calcul des Probabilites", 1888).

В круге единичного радиуса наудачу выбирается хорда. Какова вероятность того, что ее длина будет больше, чем длина стороны вписанного в круг правильного треугольника?

 

Есть по крайней мере три способа «выбрать наудачу хорду в круге». 1. Зафиксируем одну точку (конец хорды) на окружности и выберем наудачу на окружности другую точку (второй конец хорды). Здесь Ω = [0, 2π ], а благоприятными являются положения второй точки на интервале [2π /3, 4π /3] (хорды, помеченные на рисунке красным цветом). Вероятность получить «длинную» хорду равна 1/3.

 

 

2. Существует ровно одна хорда, для которой данная точка в круге является серединой (кроме того случая, когда брошенная наудачу точка попадет в центр круга. Но поскольку вероятность этого события равна нулю, то учет или неучет такого события не влияет на итоговую вероятность). Можно поэтому выбирать наудачу хорду, бросая наудачу точку (середину хорды) в круг. Здесь Ω — круг радиуса 1, μ (Ω ) = π , а благоприятными являются положения середины хорды внутри вписанного в треугольник круга (радиусом 1/2).Вероятность получить «длинную» хорду равна отношению площадей кругов, то есть 1/4.

 

3. Наконец, можно ограничиться рассмотрением только хорд, перпендикулярных какому-либо диаметру (остальные могут быть получены поворотом). То есть эксперимент может состоять в выборе середины хорды наудачу на диаметре круга — отрезке длиной 2. Благоприятными являются положения середины хорды на отрезке длиной 1. Искомая вероятность для такого эксперимента равна 1/2.

 

 

В чем причина разницы в ответах на, казалось бы, один и тот же вопрос? На самом деле формулировка задач и не корректна с математической точки зрения. «Выбор наудачу хорды в круге» может быть по-разному описан с помощью геометрического определения вероятности (что мы и сделали). То есть этот «эксперимент» можно по-разному описать с помощью выбора наудачу точки в некоторой области.

Слово «эксперимент» взято в кавычки не напрасно: сказав «в круге наудачу выбирается хорда», мы еще не описали физического эксперимента. Действительно, каждому из трех предложенных способов выбора хорд можно сопоставить конкретный физический эксперимент (всякий раз другой).

Так что парадокс исчезает сразу, как только получен ответ на вопрос: что значит «в круге наудачу выбирается хорда»?

Заканчивая обсуждение понятия геометрической вероятности, сделаем очень важное для дальнейшего замечание.

Замечание 7. Если даже эксперимент удовлетворяет геометрическому определению вероятности, далеко не для всех множеств А Í Ω вероятность может быть вычислена как отношение меры А к мере Ω . Причиной этого является существование так называемых «неизмеримых» множеств, то есть множеств, мера которых не существует.

А если не для всех подмножеств Ω мы можем определить их вероятности, следует сузить класс множеств, называемых «событиями», оставив в этом классе только те множества, для которых мы можем определить вероятность.

В следующей главе мы займемся построением (вслед за Андреем Николаевичем Колмогоровым) аксиоматики теории вероятностей: познакомимся с понятиями σ -алгебры (или поля) событий, вероятностной меры, вероятностного пространства.

Определение 12.

Пусть Ω — некоторое множество и Ψ — σ -алгебра его подмножеств. Мера μ: Ψ → R называется нормированной, если μ (Ω ) = 1. Другое название нормированной меры — «вероятность» или «вероятностная мера».

То же самое еще раз и подробно:

Определение 13.

Пусть Ω — пространство элементарных исходов и Ψ — σ -алгебра его подмножеств (событий). Вероятностью или вероятностной мерой на ( Ω, Ψ ), называется функция P Ψ → R, обладающая свойствами:

( P1 ) Для любого события А Î Ψ выполняется неравенство P(А)≥ 0;

( P2 ) Для любого счетного набора попарно несовместных событий А₁, А₂… Î Ψ имеет место равенство

( P3 ) Вероятность достоверного события равна единице: P(Ω ) = 1.

Свойства ( P1 )–( P3 ) часто называют «аксиомами вероятности».

Определение 14.

Тройка ( Ω, Ψ , Р ), в которой Ω — пространство элементарных исходов, Ψ — σ -алгебра его подмножеств и P — вероятностная мера на Ψ, называется вероятностным пространством.

Выпишем свойства вероятности:

0.

1. Для любого конечного набора попарно несовместимых событий А₁, А₂… Î Ψ имеет место равенство

2.

3. Если , то

4. Если , то

5.

6.

7.

8.

9. (2)

 

Условная вероятность

Пример 13. Кубик подбрасывается один раз. Известно, что выпало более трех очков. Какова при этом вероятность того, что выпало четное число очков?

В данном случае пространство элементарных исходов состоит из трех равновозможных элементарных исходов: Ω = {4, 5, 6}, и событию A = {выпало четное число очков} благоприятствуют 2 из них: A = {4, 6}. Поэтому P( A ) = 2/3.

Посмотрим на этот вопрос с точки зрения первоначального эксперимента. Пространство элементарных исходов при одном подбрасывании кубика состоит из шести точек: Ω = {1, 2, 3, 4, 5, 6}. Слова «известно, что выпало более трех очков» означают, что в эксперименте произошло событие B = {4, 5, 6}, . Слова «какова при этом вероятность того, что выпало четное число очков? » означают, что нас интересует, в какой доле случаев при осуществлении B происходит и А. Вероятность события А, вычисленную в предположении, что нечто о результате эксперимента уже известно (событие B произошло), мы будем обозначать через P(A/B)

Мы хотим вычислить отношение числа исходов, благоприятствующих А внутри B (то есть благоприятствующих одновременно A и B), к числу исходов, благоприятствующих B.

Определение 15. Условной вероятностью события А, при условии, что произошло событие В, называется число

Будем считать, что условная вероятность определена только в случае, когда P(В) > 0.

Следующее свойство называется " теоремой умножения":

Теорема 6. P(A∩ B) = P(B)P(A\B) = P(A)P(B\A), если соответствующие условные вероятности определены (то есть если P(В) > 0, P(A) > 0).

Теорема умножения для большего числа событий:

Теорема 7. P(A₁ ∩ A₂ ∩ …∩ A_n) = P(A₁) P(A₂\A₁) P(A₃ \A₁ ∩ A₂)… P(A_n \A₁∩ …∩ A_n-1)если соответствующие условные вероятности определены.

Независимость

Определение 16. События A и B называются независимыми, если P(A∩ B) = P(A)P(B)

Пример 14.

1. Точка с координатами ξ, η бросается наудачу в квадрат со стороной 1. Доказать, что для любых х, у Î R события A = { ξ < x } и B = { η < y } независимы.

2. Точка с координатами ξ , η бросается наудачу в треугольник с вершинами (1, 0), (0, 0) и (0, 1). Доказать, что события A = { ξ < 1/2} и B = { η < 1/2} зависимы.

 

1. Рассмотрим х, у Î [0, 1]). Видим, что P ( A ) = x, P ( B ) = y, P ( A ∩ B ) = x y, так что A = { ξ < 1/2} и B = { η < 1/2} независимы.

2. На рисунке видим, что P( A ) = 3/4, P( B ) = 3/4 P( A ∩ B ) = 1/2ч≠ (3/4)², так что события A = { ξ < 1/2} и B = { η < 1/2}  зависимы.

Замечание 8. Если события A и B несовместны, то они независимы, если и только если P ( A ) = 0 или P ( B ) = 0

Следствие 2. Если P ( B ) > 0, то события А и В независимы P (А\В) =Р(А)

Если P(А) > 0, то события А и В независимы P(В\А) =Р(В)

Лемма 1. Если события А и В независимы, то независимы и события .

Определение 17. События А₁, А₂…А _n называются независимыми в совокупности, если для любого набора

1 ≤ i₁, i₂…i_k ≤ n

)                                                                              (3)

Замечание 9. Если события А₁, А₂…А _n независимы в совокупности, то они попарно независимы, то есть любые два события А _i, А _j независимы. Достаточно в равенстве (3) взять k =2. Обратное, как показывает следующий пример, неверно.

Пример 15 (Пример С. Н. Бернштейна).

Рассмотрим правильный тетраэдр, 3 грани которого окрашены, соответственно, в красный, синий, зеленый цвета, а четвертая грань содержит все три цвета. Событие A, (B, C) означает, что выпала грань, содержащая красный (синий, зеленый) цвета.

Вероятность каждого из этих событий равна 1/2, так как каждый цвет есть на двух гранях из четырех. Вероятность пересечения любых двух из них равна 1/4, так как только одна грань содержит два цвета. А так как 1/4 = 1/2 1/2, то все события попарно независимы.

Но вероятность пересечения всех трех тоже равна 1/4, а не 1/8, то есть события не являются независимыми в совокупности.

Заметьте, что равенство (6) выполнено для k = 2, но не выполнено для k = 3.

Формула полной вероятности

Пример 16. Есть 3 завода, производящих одну и ту же продукцию. При этом 1-й завод производит 25%, 2-й завод — 35% и 3-й завод — 40% всей производимой продукции. Брак составляет 5% от продукции 1-го завода, 3% от продукции 2-го и 4% от продукции 3-го завода. Вся продукция смешивается и поступает в продажу. Найти а) вероятность купить бракованное изделие; б) условную вероятность того, что купленное изделие изготовлено 1-м заводом, если это изделие бракованное.

Первая вероятность равна доле бракованных изделий в объеме всей продукции, то есть

0, 05*0, 25 + 0, 03*0, 35 + 0, 04*0, 4.

Вторая вероятность равна доле брака 1-го завода среди всего брака, то есть

Определение 18. Набор попарно несовместных событий Н₁, Н₂… таких, что P(А _i ) > 0 для всех i и

называется полной группой событий или разбиение пространства Ω

События Н₁, Н₂ …, образующие полную группу событий, часто называют гипотезами. При подходящем выборе гипотез для произвольного события А могут быть сравнительно просто вычислены P(А/ Н _i ) (вероятность событию А произойти при выполнении «гипотезы» Н _i) и собственно P(Н _i )(вероятность выполнения «гипотезы» Н _i).

Теорема 8 ( Формула полной вероятности ).

Пусть Н₁, Н₂ — полная группа событий. Тогда вероятность любого события A может быть вычислена по формуле:

4.4 Формула Байеса

Теорема 9 ( Формула Байеса ).

Пусть Н₁, Н₂ …— полная группа событий и A — некоторое событие положительной вероятности. Тогда условная вероятность того, что имело место событие Н _k, если в результате эксперимента наблюдалось событие A, может быть вычислена по формуле:

 

Пример 17. Вернемся к примеру 15. Изделие выбирается наудачу из всей произведенной продукции. Рассмотрим три гипотезы: Н _i = {изделие изготовлено i-м заводом }, i = 1, 2, 3. Вероятности этих событий даны: P(Н₁) = 0, 25, P(Н₂) = 0, 35, P(Н₃) = 0, 4. Пусть A = {изделие оказалось бракованным }. Даны также условные вероятности P( A \Н₁) = 0, 05, P( A \Н₂) = 0, 03, P( A \Н₃) = 0, 04

Пример 18. Два стрелка подбрасывают монетку и выбирают, кто из них стреляет по мишени (одной пулей). Первый стрелок попадает по мишени с вероятностью 1, второй стрелок — с вероятностью 0, 00001. Можно сделать два предположения об эксперименте:

Н₁ = {стреляет 1-й стрелок}

Н₂ = { стреляет 2-й стрелок }.

Априорные (a’priori —«до опыта») вероятности этих гипотез одинаковы: P(Н₁) = P(Н₁) = 1/2.

Рассмотрим событие A = {пуля попала в мишень}. Известно, что

P( A \Н₁) = 1, P( A \Н₂) = 0, 00001

Поэтому вероятность пуле попасть в мишень P( A ) = 1/2*1 + 1/2*0, 00001.. Предположим, что событие A произошло. Какова теперь апостериорная (a’posteriori — «после опыта») вероятность каждой из гипотез Н _i? Очевидно, что первая из этих гипотез много вероятнее второй (а именно, в 100000 раз). Действительно,

Раздел 5. Схема Бернулли

5.1 Распределение числа успехов в n испытаниях

Определение 19. Схемой Бернулли называется последовательность независимых испытаний, в каждом из которых возможны лишь два исхода — «успех» и «неудача», при этом «успех» в одном испытании происходит с вероятность р Î [0, 1], «неудача» — с вероятностью q = 1 - p.

Теорема 10 ( Формула Бернулли ).

Обозначим через v_n число успехов в n испытаниях схемы Бернулли. Тогда для любого k = 0, 1, … n

 

Доказательство. Событие A ={ v_n = k} означает, что в n испытаниях схемы Бернулли произошло ровно k успехов. Рассмотрим один из благоприятствующих событию A  элементарных исходов:

 

Здесь буквами «у» и «н» обозначены, соответственно, успешный и неудачный результаты испытаний. Поскольку испытания независимы, вероятность такого элементарного исхода (первые k испытаний завершились успехом, остальные неудачей) равна p^k (1 - p ) ^{n - k}.

Другие благоприятствующие событию A элементарные исходы отличаются от рассмотренного выше лишь расположением k успехов на n местах. Есть ровно  способов расположить k успехов на n местах. Поэтому событие A состоит из  элементарных исходов, вероятность каждого из которых равна p^k (1 - p ) ^{n - k}.

Определение 20. Набор чисел

называется биноминальным распределением вероятностей  и обозначается В _np или B ( n, p ).

Теорема 11 Пусть m ₁, m ₂ целые числа, 0 £ m ₁ £ m £  m ₂ £ n Обозначим через Р_n(m ₁, m ₂ ) вероятность того, что событие А наступило не менее m ₁ и не более m ₂ раз в n испытаниях. Тогда

Случайные величины

Мы уже видели, что для очень многих экспериментов нет никаких различий в подсчете вероятностей событий, тогда как элементарные исходы в этих экспериментах очень различаются. Но нас и должны интересовать именно вероятности событий, а не структура пространства элементарных исходов. Поэтому пора во всех таких «похожих» экспериментах вместо самых разных элементарных исходов использовать, например, числа. То есть ввести соответствие (иначе говоря, отображение) между элементарными исходами и вещественными числами (с ними удобно работать).

Пусть имеется случайный эксперимент и задано вероятностное пространство ( Ω, Ψ , Р).

Определение 23. Функция ξ: Ω → R называется случайной величиной, если для любого х Î R множество { ξ < x } = { ω : ξ ( ω ) < x } является событием, то есть принадлежит σ -алгебре событий Ψ.

Замечание 10. Можно смело считать, что любое множество элементарных исходов есть событие, и, следовательно, случайная величина есть произвольная функция из Ω в R. Никаких неприятностей на практике это обычно не влечет.

Определение 24. Будем говорить, что функция ξ : Ω → R является Ψ -измеримой, если { ω : ξ ( ω ) < x } принадлежит Ψ для любого х Î R.

Итак, случайная величина есть Ψ - измеримая функция, ставящая в соответствие каждому элементарному исходу ω Î Ω число ξ ( ω ) Î R.

Пример 21. Подбрасываем 1 раз кубик. Пусть Ω = {1, 2, 3, 4, 5, 6}, и две функции из Ω в заданы так: ξ (ω )= ω , η (ω )= ω ².

Если Ψ есть множество всех подмножеств Ω , то ξ и η являются случайными величинами, поскольку любое множество элементарных исходов принадлежит Ψ, в том числе и {ω: ξ (ω ) < x} или {ω: η (ω ) < x}. Можно записать соответствие между значениями случайных величин ξ и η вероятностями принимать эти значения в виде «таблицы распределения вероятностей» или, коротко, «таблицы распределения»:

 

ξ	1	2	3	4	5	6
Р	1/6	1/6	1/6	1/6	1/6	1/6

 

η	1	4	9	16	25	36
Р	1/6	1/6	1/6	1/6	1/6	1/6

Здесь 1/6 = Р( ξ =1)=…= Р( ξ =6) = Р( η =1)= …= Р( η =36)

Пусть σ -алгебра событий Ψ состоит всего из четырех множеств:

Ψ = { Ω , Æ , {1, 3, 5}, {2, 4, 6} }

то есть событием является, кроме достоверного и невозможного событий, выпадение четного (соответственно, нечетного) числа очков. Убедимся, что при такой «бедной» σ -алгебре ни ξ , ни η не являются случайными величинами, так как эти функции не Ψ - измеримы. Возьмем (например) x = 3, 967. Видим, что

{ ω Î Ω: ξ ( ω ) < 3, 967}= {1, 2, 3} Ï Ψ и { ω Î Ω: η ( ω ) < 3, 967}= {1} Ï Ψ

Теперь попробуем понять, зачем нужна Ψ - измеримость и почему требуется, чтобы { ω : ξ ( ω ) < x } являлось событием.

Если задана случайная величина ξ , нам может потребоваться вычислить вероятности типа

P( ξ = 5) = P{ ω : ξ ( ω ) = 5},

P (ξ Î [-3, 7]),

P(ξ ³ 3, 2),

P( ξ > 0)

(и вообще самые разные вероятности попадания в различные множества на прямой). Это возможно только если множества, стоящие под знаком вероятности, являются событиями (напомню, что вероятность есть функция из σ - алгебры событий в [0, 1]).

Но если потребовать, чтобы A_x = { ω : ξ ( ω ) < x } было событием при любом x, то мы из свойств σ - алгебры сразу получим, что

и — событие, и — событие,

и — событие,

и { ω : ξ ( ω ) = x }= B_x \ A_x — событие,                                                                                                                (7)

и т.д., и т.п. (операции пересечения, объединения, дополнения событий не выводят из класса событий).

Можно потребовать в определении 23 чего-нибудь другого. Например, чтобы событием было попадание в любой интервал: ( ω : ξ ( ω ) Î [ a, b ]) для любых a < b.

Или чтобы { ω : ξ ( ω ) ³ x } было событием для любого x. Любое такое определение эквивалентно исходному.

Опишем различные типы распределений случайных величин. Под распределением случайной величины мы будем понимать соответствие

«значение случайной величины ↔ вероятность принимать это значение»,

либо (чаще)

«множество на прямой ↔ вероятность случайной величине попасть в это множество».

Дискретные распределения

Определение 25. Говорят, что случайная величина ξ имеет дискретное распределение, если существует конечный или счетный набор чисел { a ₁, a ₂, …} такой, что:

а) p_i = P { ξ = a_i } > 0 для всех i;

б) .

То есть случайная величина ξ имеет дискретное распределение, если она принимает не более чем счетное число значений.

Определение 26. Если случайная величина ξ имеет дискретное распределение, назовем таблицей распределения соответствие a_i ↔ p_i, которое чаще всего рисуют так:

 

ξ	а1	а2	а3	…
Р	р1	р2	р3	…

Примеры дискретных распределений

Вырожденное распределение.

Говорят, что случайная величина ξ имеет вырожденное распределение с параметром а, и пишут ξ Î I _a если ξ принимает единственное значение а с вероятностью 1, то есть P( ξ = a ) = 1. Таблица распределения ξ имеет вид

ξ	а
Р	1

 

Распределение Бернулли.

Говорят, что случайная величина ξ имеет распределение Бернулли с параметром р, и пишут ξ Î В _р, если ξ принимает значения 1 и 0 с вероятностями р и 1 - р, соответственно. Случайная величина ξ с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха (0 успехов или 1 успех). Таблица распределения ξ имеет вид

ξ	0	1
Р	(1- p )	р

 

Биномиальное распределение.

12345678Следующая ⇒

Поделиться: