ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ ПРИ РАСЧЁТЕ ЗУБЧАТЫХ ПЕРЕДАЧ
Зубья зубчатых колёс входят в зацепление поочерёдно и нагружаются по отнулевому циклу. Выбор допускаемых напряжений базируется на кривых усталости, полученных при испытании образцов – аналогов зубчатых колёс.
Кривые усталости строят в координатах наибольшее напряжение цикла  - число циклов нагружения
- число циклов нагружения  . При построении кривых усталости для контактных напряжений под разрушением подразумевают превышение предельно допустимого значения отношения площади поверхности зуба, пораженного усталостным выкрашиванием, к площади его активной поверхности.
. При построении кривых усталости для контактных напряжений под разрушением подразумевают превышение предельно допустимого значения отношения площади поверхности зуба, пораженного усталостным выкрашиванием, к площади его активной поверхности.
Как показывает опыт экспериментальных исследований, кривые усталости имеют два характерных участка: левый наклонный и правый горизонтальный (рис. 2.15,  ). Часто применяют логарифмическую шкалу для оси абсцисс. При этом наклонный участок кривой усталости заменяют прямой линией (рис. 2.15, б).
). Часто применяют логарифмическую шкалу для оси абсцисс. При этом наклонный участок кривой усталости заменяют прямой линией (рис. 2.15, б).
Кривые усталости строят для различных видов напряжений (контактных  и изгиба
и изгиба 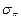 ), для различных материалов и видов термической обработки.
), для различных материалов и видов термической обработки.
Кривые усталости для контактных напряжений  приведены на рис. 2.15, в, для напряжений изгиба
приведены на рис. 2.15, в, для напряжений изгиба 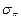 - на рис. 2.15, г.
- на рис. 2.15, г.
Число циклов нагружения
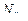
называют абсциссой точки перелома кривой усталости или базовым числом циклов нагружения (для контактных напряжений

, для напряжений изгиба
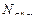
) и определяют на основании экспериментов:

;
 .
.
В формуле (2.8) средняя твёрдость поверхности зубьев  подставляется только в единицах НВ. Если средняя твёрдость поверхности зубьев
подставляется только в единицах НВ. Если средняя твёрдость поверхности зубьев  выражена в единицах HRCЭ, то следует перевести единицы HRCЭ в единицы НВ (ориентировочно 1HRCЭ ≈ 10 НВ или более точно см. табл. 2.5). При этом, если получилось
выражена в единицах HRCЭ, то следует перевести единицы HRCЭ в единицы НВ (ориентировочно 1HRCЭ ≈ 10 НВ или более точно см. табл. 2.5). При этом, если получилось 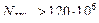 , следует принять
, следует принять 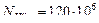 .
.
Напряжения  , соответствующие
, соответствующие  , называют пределом выносливости (для контактных напряжений
, называют пределом выносливости (для контактных напряжений  , для напряжений изгиба
, для напряжений изгиба  ).
).
 Предел контактной выносливости вычисляют по эмпирическим формулам в зависимости от материала, способа тер-мической обработки зубча-того колеса и средней твёр-дости H поверхности зубьев (см. табл. 2.4).
Предел контактной выносливости вычисляют по эмпирическим формулам в зависимости от материала, способа тер-мической обработки зубча-того колеса и средней твёр-дости H поверхности зубьев (см. табл. 2.4).
Рис. 2.15. Вид кривых усталости
При нагрузках с напряже-ниями  передача мо-жет работать практически неограниченное время, при
передача мо-жет работать практически неограниченное время, при 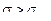 - ограниченное вре-мя. Если при расчёте Сум-марное число циклов наг-ружения
- ограниченное вре-мя. Если при расчёте Сум-марное число циклов наг-ружения  будет меньше
будет меньше  , то напряжение можно повысить до
, то напряжение можно повысить до 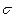 (см. рис. 2.15, б).
(см. рис. 2.15, б).
Наклонный участок кривой усталости описывают степенной функцией
 ,
,
где 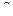 - экспериментально определяемый показатель степени уравнения кривой усталости;
- экспериментально определяемый показатель степени уравнения кривой усталости;  - константа, зависящая от свойств материала.
- константа, зависящая от свойств материала.
Для точек  и
и  (рис.2.15, б) имеем:
(рис.2.15, б) имеем:

Для одинаковых правых частей уравнений имеем:  . Откуда
. Откуда

.
Разделив обе части уравнения (2.11) на коэффициент безопасности 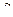 , получают допускаемые напряжения
, получают допускаемые напряжения  для числа циклов
для числа циклов  :
:

.
Величину  называют коэффициентом долговечности, учитывающим влияние ресурса передачи, и обозначают
называют коэффициентом долговечности, учитывающим влияние ресурса передачи, и обозначают  при расчёте на сопротивление контактной усталости активных поверхностей зубьев и
при расчёте на сопротивление контактной усталости активных поверхностей зубьев и  - при расчёте на сопротивление усталости зубьев при изгибе.
- при расчёте на сопротивление усталости зубьев при изгибе.
На основании формулы (2.12) определяют допускаемые контактные напряжения  (в обозначениях - индекс Н) и допускаемые напряжения изгиба
(в обозначениях - индекс Н) и допускаемые напряжения изгиба  (в обозначениях – индекс F) при расчёте передачи на сопротивление усталости:
(в обозначениях – индекс F) при расчёте передачи на сопротивление усталости:

В формуле (2.14) дополнительно вводится коэффициент  , учитывающий влияние двустороннего приложения нагрузки (реверса). Рекомендации по назначению
, учитывающий влияние двустороннего приложения нагрузки (реверса). Рекомендации по назначению  см. далее.
см. далее.
Коэффициенты долговечности  и
и  :
:

, при условии

;

, при условии

.
При твёрдости активных поверхностей зубьев Н 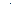 350 НВ (нормализация, улучшение):
350 НВ (нормализация, улучшение):



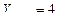 .
.
При Н> 350 НВ (закалка ТВЧ, цементация, азотирование):



 .
.
Для длительно работающих передач при большом заданном ресурсе  и, следовательно,
и, следовательно, 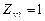 и
и  , что и учитывает первый знак неравенств в формулах (2.15) и (2.16) (т.е. на горизонтальном участке кривой усталости наибольшие напряжения равны пределу выносливости
, что и учитывает первый знак неравенств в формулах (2.15) и (2.16) (т.е. на горизонтальном участке кривой усталости наибольшие напряжения равны пределу выносливости  ). Второй знак неравенств ограничивает допускаемые напряжения по условию предотвращения пластической деформации или хрупкого разрушения зуба.
). Второй знак неравенств ограничивает допускаемые напряжения по условию предотвращения пластической деформации или хрупкого разрушения зуба.
При переменных режимах нагружения (см., например, циклограмму на рис. 2.14,  ) расчёт коэффициентов долговечности
) расчёт коэффициентов долговечности  и
и  выполняют по эквивалентному числу циклов нагружения
выполняют по эквивалентному числу циклов нагружения  . При этом в формуле (2.15)
. При этом в формуле (2.15)  заменяют
заменяют 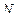 , а в формуле (2.16)
, а в формуле (2.16) 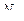 заменяют
заменяют  . Расчёт
. Расчёт  и
и  проводят отдельно для шестерни и колеса по формулам (2.6) и (2.7).
проводят отдельно для шестерни и колеса по формулам (2.6) и (2.7).
Для проверки статической прочности зубьев передачи при действии пиковой нагрузки (при кратковременной перегрузке), не учтённой при расчёте на сопротивление усталости, по табл. 2.4 определяют предельные допускаемые контактные напряжения  , не вызывающие остаточных деформаций или хрупкого разрушения поверхностного слоя, а также предельные допускаемые напряжения изгиба
, не вызывающие остаточных деформаций или хрупкого разрушения поверхностного слоя, а также предельные допускаемые напряжения изгиба 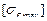 , не вызывающие остаточных деформаций или хрупкого излома зуба пиковой нагрузкой.
, не вызывающие остаточных деформаций или хрупкого излома зуба пиковой нагрузкой.
Рассмотрим подробнее определение допускаемых напряжений при расчёте зубчатых передач.
Допускаемые контактные напряжения 
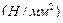 при расчете зубчатой передачи на сопротивление контактной усталости активных поверхностей зубьев определяют отдельно для шестерни (индекс 1) и колеса (индекс 2):
при расчете зубчатой передачи на сопротивление контактной усталости активных поверхностей зубьев определяют отдельно для шестерни (индекс 1) и колеса (индекс 2):

,
где  – предел контактной выносливости активной поверхности зубьев шестерни (колеса), соответствующий абсциссе точки перелома кривой усталости для контактных напряжений
– предел контактной выносливости активной поверхности зубьев шестерни (колеса), соответствующий абсциссе точки перелома кривой усталости для контактных напряжений  и принимаемый по табл. 2.4 в зависимости от материала и термообработки зубьев шестерни (колеса),
и принимаемый по табл. 2.4 в зависимости от материала и термообработки зубьев шестерни (колеса), 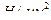 ;
;  – коэффициент безопасности (табл. 2.4);
– коэффициент безопасности (табл. 2.4);  – коэффициент долговечности, учитывающий влияние ресурса передачи при расчете на сопротивление контактной усталости.
– коэффициент долговечности, учитывающий влияние ресурса передачи при расчете на сопротивление контактной усталости.
Коэффициент долговечности  определяют отдельно для шестерни и колеса, сопоставляя эквивалентное число циклов нагружения
определяют отдельно для шестерни и колеса, сопоставляя эквивалентное число циклов нагружения  , рассчитанное по формуле (2.6), с базовым числом циклов нагружения
, рассчитанное по формуле (2.6), с базовым числом циклов нагружения  (абсциссой точки перелома кривой усталости для контактных напряжений). При этом
(абсциссой точки перелома кривой усталости для контактных напряжений). При этом  следует определить отдельно для шестерни и колеса:
следует определить отдельно для шестерни и колеса:
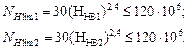
Как уже указывалось ранее, в формулу (2.18) средняя твердость поверхности зубьев HHB1(2) подставляется только в единицах НВ. Если средняя твердость поверхности зубьев шестерни (колеса) НHRCэ выражена в единицах HRCЭ, то следует перевести единицы HRCЭ в единицы НВ (ориентировочно 1 HRCЭ =10НВ или более точно см. табл. 2.5). При этом, если для шестерни или колеса получилось  , то следует принять
, то следует принять  .
.
Таким образом, если в результате расчета для шестерни мы получили 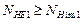 , то коэффициент долговечности
, то коэффициент долговечности 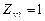 . Если для шестерни получено
. Если для шестерни получено  , то коэффициент долговечности рассчитывают по формуле:
, то коэффициент долговечности рассчитывают по формуле:

.
Аналогичным образом поступают и для колеса. При 
 . При
. При 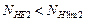 :
:

.
В формулах (2.19)…(2.20):  при
при  и
и  при
при  .
.
Если в результате расчета по формулам (2.19) и (2.20) получили  , то следует принять
, то следует принять  .
.
После определения допускаемых контактных напряжений для шестерни  и колеса
и колеса  принимают допускаемые контактные напряжения
принимают допускаемые контактные напряжения  для передачи в сборе, называемые иногда расчётными допускаемыми контактными напряжениями. При этом назначение
для передачи в сборе, называемые иногда расчётными допускаемыми контактными напряжениями. При этом назначение  зависит от вида зубьев передачи (прямые или непрямые), а также средней твёрдости их активных поверхностей
зависит от вида зубьев передачи (прямые или непрямые), а также средней твёрдости их активных поверхностей 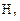 и
и 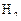 . К зубчатым передачам с непрямыми зубьями относят цилиндрические передачи с косыми и шевронными зубьями, а также конические передачи с круговыми зубьями.
. К зубчатым передачам с непрямыми зубьями относят цилиндрические передачи с косыми и шевронными зубьями, а также конические передачи с круговыми зубьями.
Рассмотрим рекомендации различных авторов по назначению  для передачи, т.е. зубчатой пары, при известных величинах
для передачи, т.е. зубчатой пары, при известных величинах  и
и  :
:
1) авторы учебника [4] и О.П.Леликов [7]:
для зубчатых передач с прямыми зубьями (цилиндрических и конических)
 ,
,
где  - меньшее из двух:
- меньшее из двух:  ,
,  ;
;
для зубчатых передач с непрямыми зубьями (цилиндрических и конических) в связи с расположением линии контакта под углом к полюсной линии допускаемые напряжения для передачи

можно повысить до значения

при выполнении условий

- для цилиндрической передачи;
 - для конической передачи,
- для конической передачи,
где  - см. формулу (2.21).
- см. формулу (2.21).
Если при расчёте  по формуле (2.22) получилось
по формуле (2.22) получилось 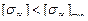 , то следует принять
, то следует принять  .Если получилось
.Если получилось 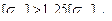 для цилиндрической передачи или
для цилиндрической передачи или  для конической передачи, то согласно условий (2.23) и (2.24) следует принять соответственно
для конической передачи, то согласно условий (2.23) и (2.24) следует принять соответственно 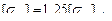 и
и  .
.
ГОСТ 21354–87 “Передачи зубчатые цилиндрические эвольвентные внешнего зацепления. Расчёт на прочность” также рекомендует назначать 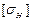 для цилиндрической передачи с прямыми зубьями по условию (2.21), а с косыми и шевронными зубьями по формуле (2.22) с обязательным соблюдением условия (2.23);
для цилиндрической передачи с прямыми зубьями по условию (2.21), а с косыми и шевронными зубьями по формуле (2.22) с обязательным соблюдением условия (2.23);
2) Л.В.Курмаз и А.Т.Скойбеда [2]:
для цилиндрических передач с небольшим отклонением твердостей активных поверх-ностей зубьев ( 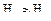 ) рекомендуется принимать
) рекомендуется принимать  по условию (2.21);
по условию (2.21);
для цилиндрических и конических передач со значительным отличием твердостей активных поверхностей зубьев (

) следует принять

с выполнением условий
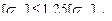
- для цилиндрической передачи;
 - для конической передачи,
- для конической передачи,
где  - меньшее из двух:
- меньшее из двух:  ,
,  ;
;
3) Д.Н.Решетов [6]:
для зубчатых передач с прямыми и непрямыми зубьями (цилиндрических и конических) при твёрдости активной поверхности зубьев колеса зубчатой пары менее 350 НВ при перепаде средних твердостей  НВ и при окружной скорости менее 20
НВ и при окружной скорости менее 20  (условие прирабатываемости) допускаемые напряжения для передачи
(условие прирабатываемости) допускаемые напряжения для передачи  можно назначать по формуле (2.22) с обязательным соблюдением условия (2.23) для цилиндрической передачи и условия (2.24) для конической передачи. Во всех остальных случаях для данных зубчатых передач рекомендуется принимать
можно назначать по формуле (2.22) с обязательным соблюдением условия (2.23) для цилиндрической передачи и условия (2.24) для конической передачи. Во всех остальных случаях для данных зубчатых передач рекомендуется принимать  по условию (2.21);
по условию (2.21);
4) П.Ф.Дунаев и О.П. Леликов [3]:
для зубчатых передач с прямыми зубьями (цилиндрических и конических) рекомендуется принимать  по условию (2.21);
по условию (2.21);
для зубчатых передач с непрямыми зубьями (цилиндрических и конических) допускаемые напряжения для пары зубчатых колёс

можно повысить до значения

при выполнении условия (2.23) для цилиндрической передачи и условия (2.24) для конической передачи;
5) М.Н.Иванов [1]:
для зубчатых передач с прямыми зубьями (цилиндрических и конических) следует назначать  по условию (2.21);
по условию (2.21);
для зубчатых передач с непрямыми зубьями (цилиндрических и конических) при твердостях активных поверхностей зубьев 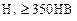 и
и  следует назначать
следует назначать  по условию (2.21);
по условию (2.21);
для зубчатых передач с непрямыми зубьями (цилиндрических и конических) при 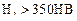 и
и  (например, для варианта термообработки ׀ ׀, см. табл. 2.2) допускаемые напряжения для зубчатой пары
(например, для варианта термообработки ׀ ׀, см. табл. 2.2) допускаемые напряжения для зубчатой пары  можно повысить до значения, определяемого по формуле (2.25) с обязательным соблюдением условием (2.26) для цилиндрической передачи и условия (2.27) для конической передачи.
можно повысить до значения, определяемого по формуле (2.25) с обязательным соблюдением условием (2.26) для цилиндрической передачи и условия (2.27) для конической передачи.
Таблица 2.4 – Величины 
| Термообработка
| Марки сталей
| 
| 
| 
| 
| 
| 
|
| Улучшение
|
45, 40Х,
35ХМ, 40ХН и др.
| 2ННВ + 70
| 1, 1
| 1, 75ННВ
| 1, 7
| 2, 8 
| 2, 74ННВ
|
Улучшение+
+закалка ТВЧ (модуль  ) )
| 40Х,
35ХМ,
40ХН
| 17НHRCэПОВ + 200
| 1, 2
| 650
| 1, 7
| 40НHRCэПОВ
| 1260
|
Улучшение+
+закалка ТВЧ (модуль  ) )
| 550
| 1430
|
| Улучшение+
+цементация+
+закалка
|
20Х, 20ХНМ,
12ХН3А, 18ХГТ,
25ХГМ
| 23 НHRCэПОВ
| 1, 2
| 750
| 1, 5
| 40НHRCэПОВ
| 1200
|
| Улучшение+
+нитроцементация+
+закалка
|
25ХГМ,
25ХГНМ
| 23 НHRCэПОВ
| 1, 2
| 1000
| 1, 5
| 40НHRCэПОВ
| 1520
|
| 25ХГТ, 30ХГТ,
35Х и др.
| 750
|
| Улучшение+
+азотирование
|
38Х2Ю, 38Х2МЮА
| 1050
| 1, 2
| 12НHRCэСЕРДЦ + 290
| 1, 7
| 40НHRCэПОВ
| 1000
|
| 40Х, 40ХФА,
40ХНМА и др.
| 30НHRCэПОВ
|
| Примечание. ННВ – средняя твердость активной поверхности зуба в единицах НВ; НHRCэПОВ – средняя твердость активной поверхности зуба в единицах HRCЭ; HHRCэСЕРДЦ – средняя твердость сердцевины зуба в единицах HRCЭ;  - предел текучести (табл. 2.1) - предел текучести (табл. 2.1)
|
Таблица 2.5 – Соотношения твердостей, выраженных в единицах HRC Э и НВ
| HRCЭ
| 45
| 47
| 48
| 50
| 52
| 53
| 55
| 60
| 63
| 65
|
| НВ
| 427
| 450
| 460
| 484
| 504
| 515
| 540
| 611
| 640
| 668
|
Повышение допускаемых напряжений 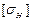 для зубчатой пары с непрямыми зубьями при
для зубчатой пары с непрямыми зубьями при 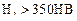 и
и 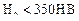 связано с так называемым головочным эффектом. Как известно, ножка зуба, как поверхность отстающая, обладает меньшей стойкостью против выкрашивания, чем головка, как поверхность опережающая. Поэтому ножка зуба колеса, работающая с головкой зуба шестерни, начинает выкрашиваться и изнашиваться в первую очередь. Но так как линия контакта при непрямом зубе (например, косом) наклонена к полюсной линии и проходит по поверхности ножки и головки зуба, то в результате местного изнашивания ножки колеса происходит перераспределение давления по контактной линии и большая нагрузка передается на головку зуба колеса. При этом слабая ножка колеса разгружается, и выкрашивание прекращается. Увеличение давления между головкой зуба колеса и ножкой зуба шестерни не опасно, так как прочность активной поверхности зубьев шестерни значительно выше (
связано с так называемым головочным эффектом. Как известно, ножка зуба, как поверхность отстающая, обладает меньшей стойкостью против выкрашивания, чем головка, как поверхность опережающая. Поэтому ножка зуба колеса, работающая с головкой зуба шестерни, начинает выкрашиваться и изнашиваться в первую очередь. Но так как линия контакта при непрямом зубе (например, косом) наклонена к полюсной линии и проходит по поверхности ножки и головки зуба, то в результате местного изнашивания ножки колеса происходит перераспределение давления по контактной линии и большая нагрузка передается на головку зуба колеса. При этом слабая ножка колеса разгружается, и выкрашивание прекращается. Увеличение давления между головкой зуба колеса и ножкой зуба шестерни не опасно, так как прочность активной поверхности зубьев шестерни значительно выше ( 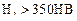 ). Однако такое перераспределение давления вдоль линии контакта зубьев наблюдается только при окружной скорости до 20
). Однако такое перераспределение давления вдоль линии контакта зубьев наблюдается только при окружной скорости до 20 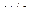 . При больших скоростях обеспечивается безысносная работа передачи и перераспределение давления не наблюдается [6].
. При больших скоростях обеспечивается безысносная работа передачи и перераспределение давления не наблюдается [6].
Допускаемые напряжения изгиба 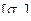 (
( 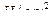 ) при расчете на сопротивление усталости зубьев при изгибе определяют отдельно для шестерни (индекс 1) и для колеса (индекс 2) по формуле:
) при расчете на сопротивление усталости зубьев при изгибе определяют отдельно для шестерни (индекс 1) и для колеса (индекс 2) по формуле:

,
где  – предел выносливости зубьев шестерни (колеса) по напряжениям изгиба, соответствующий абсциссе точки перелома кривой усталости для напряжений изгиба
– предел выносливости зубьев шестерни (колеса) по напряжениям изгиба, соответствующий абсциссе точки перелома кривой усталости для напряжений изгиба  и принимаемый по таблице 2.4 в зависимости от материала и термообработки зубьев шестерни (колеса),
и принимаемый по таблице 2.4 в зависимости от материала и термообработки зубьев шестерни (колеса),  ;
;  – коэффициент безопасности (табл. 2.4);
– коэффициент безопасности (табл. 2.4);  – коэффициент долговечности, учитывающий влияние ресурса передачи (см. ниже);
– коэффициент долговечности, учитывающий влияние ресурса передачи (см. ниже);  – коэффициент, учитывающий двустороннее приложение нагрузки. При одностороннем приложении нагрузки (привод нереверсивный)
– коэффициент, учитывающий двустороннее приложение нагрузки. При одностороннем приложении нагрузки (привод нереверсивный)  . При двустороннем приложении нагрузки (привод реверсивный) цикл нагружения – знакопеременный и предел выносливости по напряжениям изгиба меньше, чем при отнулевом (пульсирующем) цикле, характерном для нереверсивного привода. Поэтому при двустороннем приложении нагрузки принимают:
. При двустороннем приложении нагрузки (привод реверсивный) цикл нагружения – знакопеременный и предел выносливости по напряжениям изгиба меньше, чем при отнулевом (пульсирующем) цикле, характерном для нереверсивного привода. Поэтому при двустороннем приложении нагрузки принимают:  – для улучшенных сталей,
– для улучшенных сталей,  – для цементованных, закаленных ТВЧ,
– для цементованных, закаленных ТВЧ, 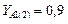 – для азотированных сталей. При курсовом проектировании к нереверсивным относят приводы ленточных и цепных конвейеров, а также элеваторов, к реверсивным – механические приводы без приводных валов и грузоподъемные лебедки.
– для азотированных сталей. При курсовом проектировании к нереверсивным относят приводы ленточных и цепных конвейеров, а также элеваторов, к реверсивным – механические приводы без приводных валов и грузоподъемные лебедки.
Коэффициент долговечности  при расчете на сопротивление усталости зубьев при изгибе, определяют отдельно для зубьев шестерни и колеса, сопоставляя эквивалентное число циклов нагружения
при расчете на сопротивление усталости зубьев при изгибе, определяют отдельно для зубьев шестерни и колеса, сопоставляя эквивалентное число циклов нагружения  , рассчитанное по формуле (2.7), с базовым числом циклов нагружения
, рассчитанное по формуле (2.7), с базовым числом циклов нагружения  (абсциссой точки перелома кривой усталости для напряжения изгиба).
(абсциссой точки перелома кривой усталости для напряжения изгиба).
Испытания показали, что для всех марок сталей независимо от вида применяемой термообработки 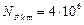 . Тогда
. Тогда  .
.
Если для шестерни получено соотношение  , то коэффициент долговечности
, то коэффициент долговечности 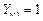 . При
. При  коэффициент долговечности следует рассчитать по формуле:
коэффициент долговечности следует рассчитать по формуле:
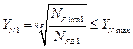
.
Аналогичным образом поступают при определении коэффициента долговечности  для колеса. Если получено соотношение
для колеса. Если получено соотношение  , то следует принять
, то следует принять  . При
. При  коэффициент долговечности
коэффициент долговечности  определяют по формуле:
определяют по формуле:
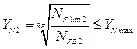
.
В формулах (2.30) … (2.31):
 ;
;  – при твёрдости активной поверхности зубьев рассматриваемого зубчатого колеса (шестерни или колеса) Н
– при твёрдости активной поверхности зубьев рассматриваемого зубчатого колеса (шестерни или колеса) Н  350НВ;
350НВ;
 ;
; 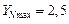 – при твердости активной поверхности зубьев рассматриваемого зубчатого колеса (шестерни или колеса) Н> 350НВ.
– при твердости активной поверхности зубьев рассматриваемого зубчатого колеса (шестерни или колеса) Н> 350НВ.
Если в результате расчёта по формулам (2.30) и (2.31) получено  , то следует принять
, то следует принять  .
.
Предельные допускаемые контактные напряжения  (
( 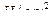 ) и напряжения изгиба
) и напряжения изгиба 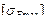 (
( 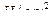 ) при расчёте зубчатой передачи на статическую прочность зубьев в момент действия пиковой нагрузки (при кратковременной перегрузке) принимают по таблице 2.4 в зависимости от вида термообработки соответствующего зубчатого колеса. При этом отдельно для шестерни и колеса определяют
) при расчёте зубчатой передачи на статическую прочность зубьев в момент действия пиковой нагрузки (при кратковременной перегрузке) принимают по таблице 2.4 в зависимости от вида термообработки соответствующего зубчатого колеса. При этом отдельно для шестерни и колеса определяют  и
и  , а также
, а также  и
и  .
.
Для зубчатой пары величина 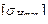 при проверке контактной прочности передачи по условию (2.3) принимается как меньшее значение из двух:
при проверке контактной прочности передачи по условию (2.3) принимается как меньшее значение из двух:  ,
,  .
.
Расчёт на прочность зубьев при изгибе пиковой нагрузкой проводят по условию (2.4) отдельно для шестерни и колеса.
Действие пиковых нагрузок оценивают коэффициентом перегрузки  , где
, где  – пиковый момент;
– пиковый момент;  – номинальный (максимальный из длительно действующих) момент, по которому проводят расчёты на сопротивление усталости.
– номинальный (максимальный из длительно действующих) момент, по которому проводят расчёты на сопротивление усталости.
Если режим нагружения задан в виде циклограммы моментов, то коэффициент перегрузки 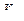 указывается в циклограмме.
указывается в циклограмме.
В случае использования типовых режимов нагружения величина 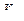 указывается отдельно, так как в типовые режимы не включают пиковые нагрузки.
указывается отдельно, так как в типовые режимы не включают пиковые нагрузки.
Если пиковый момент  по какой-либо причине не указан, то его можно принимать равным максимальному моменту электродвигателя или предельному моменту предохранительных устройств привода.
по какой-либо причине не указан, то его можно принимать равным максимальному моменту электродвигателя или предельному моменту предохранительных устройств привода.


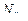 называют абсциссой точки перелома кривой усталости или базовым числом циклов нагружения (для контактных напряжений
называют абсциссой точки перелома кривой усталости или базовым числом циклов нагружения (для контактных напряжений  , для напряжений изгиба
, для напряжений изгиба 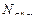 ) и определяют на основании экспериментов:
) и определяют на основании экспериментов:
 ;
;
 .
.

 , при условии
, при условии  ;
;
 , при условии
, при условии  .
.
 ,
,
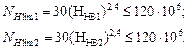
 .
.
 .
.
 можно повысить до значения
можно повысить до значения
 - для цилиндрической передачи;
- для цилиндрической передачи;
 ) следует принять
) следует принять
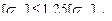 - для цилиндрической передачи;
- для цилиндрической передачи;
 можно повысить до значения
можно повысить до значения
 ,
,
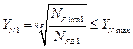 .
.
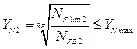 .
.