
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Содержательное описание моделей коллективного страхования космических программ
Модель 1. Первый граф (см. рис. 12) характеризует ситуацию взаимного страхования потребителя и владельца средств СЭ и в данном исследовании не рассматривается как модель с двумя участниками страхования. Модель 2. Данная модель предполагает наличие страховых отношений только между владельцем объекта страхования (первичным потребителем ожидаемого выходного эффекта, П) и страховщиком, С. Так как в модели отсутствует непосредственное отношение З Предполагается, что П страхует только свои прямые расходы C, которые он затрачивает реализацию проекта, причем выплата прибыли З ( S Э ) производится авансом перед проведением работ и при возникновении страхового случая может быть взыскана в пользу страховщика в составе стоимости C. С учетом этих предположений модель страхования задается уравнениями ожидаемых доходов субъектов страхования. При наличии договора страхования между П и С с нетто-ставкой a П и страхуемой суммой ( C ) ожидаемые доходы субъектов П, З и С находятся как математические ожидания по распределению вероятностей возможных исходов запуска КА. При благоприятном исходе П получает доход: или равный ожидаемым доходам от реализации проекта ( S А ) за вычетом расходов на реализацию проекта ( C ) и страховой премии ( a П *C ). Предполагается, что размер ожидаемых доходов S А составляет величину, достаточную для покрытия издержек на обеспечение реализации проекта. При неблагоприятном исходе S А = 0, расходы на подготовку возмещаются страховщиком и доход равен:
Вероятность первого события равна P, второго – (1 – P ) и тогда: W П = P * [SA – C * (1 + a П )] + (1 – P ) * (- a П * С) = = P * SA – ( a П + P) * C. Ожидаемый доход З находится с учетом сделанного предположения о предварительной оплате владельцем объекта страхования стоимости затрат C ЭР и прибыли S Э, а также возможности регрессного иска со стороны страховой компании при неблагоприятном исходе по вине З. При неблагоприятном исходе реализации проекта, т.к. величина a П * C уже оплачена страховщику, величина иска может составлять (1- a П ) * C, т.е. при наступлении страхового случая по вине З его доход равен: C Э – (1 – a П ) * C. В случае же наступления страхового случая, приведшего к потере объекта страхования при отсутствии эксплуатационной ошибки: C Э. При благоприятном исходе доход З равен СЭ. Вероятности событий в указанных случаях составляют: первого события Q Э, второго – ( Q – Q Э ) и третьего – P. Ожидаемый доход З в результате подготовки будет равен: W З = (P + Q – Q Э ) * C Э + Q Э *[C Э – (1 + a П ) * С] = = C Э – Q Э * (1 + a П ) * С. В данной модели для С рассматривается возможные исходы, отличающиеся по ожидаемому доходу, с вероятностями соответственно: P – успешная реализация проекта страхования (1 – P ) – потеря объекта страхования по любой причине с компенсацией ущерба владельцу объекта страхования, Q Э – потеря объекта страхования по вине З с взысканием части ущерба в пользу С. Ожидаемый доход С составит: Wc = C *( a П *P – Q + Q Э – Q Э * a П). Полученные выражения можно свести в систему, которая будет полностью описывать взаимоотношения субъектов страхования в условиях предположений, сделанных для второй модели.
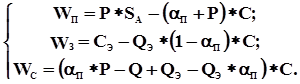
В рассматриваемой модели максимальные возможные доходы в одном договоре выражаются величинами:
При этом минимальные доходы (максимальные потери) могут составлять:
Примечание: отрицательная величина доходов означает потери. В качестве условия экономической целесообразности вступления в отношения страхования в качестве субъектов можно рассматривать требование неотрицательности средних ожидаемых доходов П, З и С по итогам запуска РКН:
Разрешая эти неравенства с учетом соотношений (2) относительно a П, получим выражения для построения областей предпочтения участников страхования, сведенные в систему:
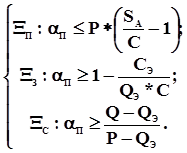
Ранее отмечалось, что норма прибыли П от договора страхования должна быть достаточной по крайней мере для покрытия необходимых издержек, т. е.:
Сопоставляя полученные выражения, можно сделать вывод о противоположности страховых интересов субъектов З, С и П. Однако, их совместное решение позволяет выделить в пространстве параметров модели область W ПС возможного достижения компромисса между П и С относительно значения a П. На рис. 13 она показана как пересечение областей X П и X С безусловного предпочтения П и С при назначении ставки страхования. При этом интересы З принимаются в расчет как ограничения только в случае его существенной ненадежности как исполнителя работ (при Q Э > C Э /C, что не соответствует накопленной практике). Его заинтересованность в повышении страховой ставки a П определяется стремлением переложить часть расходов по возмещению ущерба, связанного с потерей объекта страхования, на П. Для упрощения расчетов будем считать, что величиной Q Э можно пренебречь.
Рис. 13. Область возможного достижения компромисса Из качественного анализа соотношений (3) следует, что при выборе значения a П для П определяющей в основном является величина нормы прибыли N П, в то время как для С ограничивающими являются только надежностные характеристики. С учетом сделанных ранее предположений найдем граничные условия принятия согласованного решения относительно величины a П, соответствующего минимальным уровням претензий договаривающихся сторон. Для фиксированной нормы прибыли N П заключение договора страхования для П будет иметь смысл только при выполнении минимального требования:
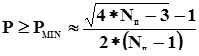 . .
Очевидно, что с ростом N П уровень требований к P со стороны П может быть ослаблен. Например, при норме прибыли П N П = 1, 1 показатель успешности должен быть не ниже 0, 92, тогда как для значений N П, равных 1, 2 и 1, 5 граничные значения PMIN составят 0, 85 и 0, 73 соответственно. Для С снижение требования к P приведет к необходимости соответствующего увеличения страховой ставки a П в соответствии с (3). Для достигнутого в процессе использования объекта страхования значения P существует минимальный уровень нормы прибыли, определяющий нижнюю границу стоимости выходного эффекта объекта страхования для вторичных потребителей:
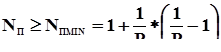 . .
Так, для значения показателя успешности использования объекта страхования P = 0, 9 уровень нормы прибыли П не должен быть ниже минимального N ПMIN = 1, 12. При снижении значения показателя P до 0, 8 субъект П вынужден будет поднять цену выходного эффекта функционирования объекта страхования таким образом, чтобы обеспечить N П не менее N ПMIN = 1, 3. Модель 3. Модель данного типа может быть рассмотрена для случая, когда в договоре на реализацию проекта указано обязательство З перед П осуществить за свой счет повторную реализацию проектов в случае неудачи предыдущих. З страхуется от своих возможных потерь, связанных с повторными реализациями. В этой модели З берет на себя весь риск, связанный с неудачным осуществлением проекта. (Но за такую привилегию П, очевидно, должен увеличить размер оплаты услуг эксплуатирующей организации, т. е. повышение S Э ). Предполагается, что З получает от П в ответственное распоряжение объект страхования, осуществляет эксплуатацию объекта, получая за это с П в качестве выплаты величину, равную C Э. Причем, З не имеет права регрессного иска к поставщикам объекта страхования. Если не учитывать возможные потери П, связанные с временем ожидания повторной реализации проекта (выплата неустойки вторичным потребителям, замораживание и связанное с этим уменьшение будущих доходов приведенных к текущему моменту времени и т.д.), то его доход абсолютно гарантирован и всегда равен W П =SA – C. В сделанных предположениях ожидаемый доход З находится следующим образом. Если первый же первая реализация оказалась успешной, то доход З будет равен величине C Э, уменьшенной на размер страховой премии a З * C. Предполагается, что страховая сумма покрывает стоимость вынужденных затрат З на проведение повторной реализации. Если же первая реализация неудачена, то З получает от С страховое покрытие C, осуществляет все необходимые затраты, связанные с повторным осуществлением проекта (включая закупку объекта страхования, а также выплату повторной страховой премии). Для абстрактного случая неограниченного числа повторных запусков ожидаемые доходы З находятся в виде суммы: W З = P * (C Э – a З * C ) + P * (1 – P ) * (C Э – 2 * a З * C ) + P * * (1 – P )2 * (C Э – 3 * a З * C ) +... + P * (1 – P )Т-1 * (СЭ – Т * a З * С) + +... = Т.к.
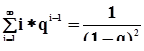 , (q < 1), то , (q < 1), то 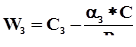 . .
Доходы страховщика в общем случае находятся в виде суммы ряда: W С = P * a З * C + P * (1 – P ) * (2 * a З * C – С) + P * (1 – P )2 *
* (Т * a З * С – (Т – 1) * С) + +... = Таким образом, полная модель страхования для рассматриваемого случая задается системой уравнений:
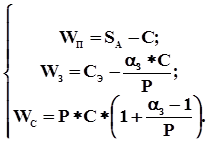
Для практики представляет интерес частный случай ограничения действия договора страхования требованием проведения не более одного повторной реализации. Средние доходы участников операции страхования проекта определяются следующими соотношениями:
В частном случае рассматриваемой модели максимальные потери (минимальные доходы) могут составлять:
Для З и С наихудший исход в общем (абстрактном) случае означает полное разорение. Максимальные возможные доходы в одной реализации выражаются величинами:
Требование неотрицательности средних доходов П, З и С по итогам реализации:
как условие экономической целесообразности их вступления в отношения страхования в качестве субъектов, позволяет построить систему безусловных требований к величине a З:
При противоположности страховых интересов субъектов З и С в пространстве параметров модели существует область W ЗС возможного достижения компромисса между З и С относительно значения a З. Из соотношений (8) следует, что при выборе значения a З для З определяющей в основном является доля эксплуатирующей организации C Э /C = d Э в структуре затрат П на реализацию проекта, для С, также как и в Модели 1, ограничивающими являются только надежностные характеристики. Найдем граничные условия принятия согласованного решения относительно величины a П с учетом сделанных ранее предположений, соответствующего минимальным уровням претензий договаривающихся сторон. Для фиксированной доли d Э заключение договора страхования реализации проекта для З будет практически всегда иметь смысл, т. к.:
Для значения P существует минимальный уровень доли d ЭMIN, определяющий нижнюю границу стоимости услуг эксплуатирующей организации:
На практике это означает, что, например, для P = 0, 8 доля ЭО в структуре затрат не может быть ниже минимального уровя d ЭMIN = 0, 24. Очевидно, что повышение надежности и качества работы эксплуатирующей организации позволят повысить вес прибыли S Э в общем объеме доходов З. Модель 4. Отношения между участниками выполнения программы характеризуются следующими положениями: П страхует потерю ожидаемого дохода вследствие задержки начала получения выходного эффекта от реализации проекта. Предполагается, что при своевременной реализации проекта потери П равны нулю, а при повторной реализации через время t потери приближенно равны:
где g – показатель, характеризующий строгость штрафных санкций к П со стороны вторичных (конечных) потребителей выходного эффекта, K – коэффициент, определяющий размерность (например, руб/сут). При расчетах принято, что время задержки получения выходного эффекта и величина потерь фиксированы ( DS А ( t )= DS А ); при последующих неудачных реализациях потери растут пропорционально их количеству. Считается, что полученная от С компенсация целиком расходуется на расчеты со вторичными потребителями. Договор страхования содержит условие неизменности страховой ставки и распространяется на серию пусков в соответствии с принятой программой. З несет полную ответственность за неудачную реализацию. Он страхует стоимость реализации проекта (без прибыли) и по условию договора с П обязан в случае необходимости провести повторную реализацию за счет собственных средств для обеспечения полного выполнения программы. П выплачивает З прибыль S Э только после успешной реализации программы. Модель 4.1. Случай неограниченной компенсации (повторные реализации проводятся до достижения успеха, абстрактная схема). Ожидаемый доход П определяется выражением:
Рациональному подходу П к назначению страховой ставки a П соответствует минимальное требование:
где Очевидно, что интерес П в наибольшей степени влияет на величину ставки страхования потери ожидаемого дохода при росте нормативной величины DS А ( dS А ). Параметры P и N П в данном случае не играют определяющей роли. Так, для P = 0, 9, N П = 1, 5 и dS А = 0, 2 величина страховой ставки ограничивается сверху уровнем 1, 0, т. е. практически ограничение отсутствует (в смысле влияния на выбор разумного значения a П ). Величина W З определяется аналогично и равна:
Минимальное требование к величине страховой ставки a З со стороны З выражается неравенством:
где
Например, для значений P = 0, 9, D Э = 0, 05 и D ЭР = 0, 15 уровень страховой ставки a З Рассмотрим доходы страховщика. В соответствии с общей схемой они будут выражаться следующим образом:
С точки зрения С уровни страховых ставок должны обеспечивать в среднем по крайней мере неотрицательность его доходов, т. е.:
При равенстве страховых ставок a З = a П = a ограничение носит тривиальный характер a ³ 1 – P. Окончательно модель 4.1 принимает вид:
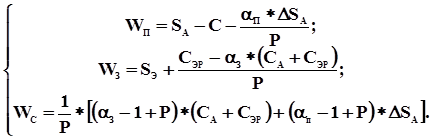
Модель 4.2. Случай ограниченной компенсации (при возникновении страхового случая проводится одна повторная реализация; в случае его неудачи З возвращает П стоимость объекта страхования). С учетом вновь введенных условий, модель доходов участников страховой операции будет представлена следующей системой уравнений:
Из рассмотрения требования неотрицательности средних доходов П, З и С по итогам реализации проекта:
как условия экономической целесообразности их вступления в отношения страхования в качестве субъектов, вытекает система требований к величинам a П и a З, на основании которых можно построить области допустимых решений. При этом, исходя из общих для всех субъектов условий возникновения страхового события, достаточно рассмотреть случай равенства страховых ставок П и З ( a З = a П = a ).
или
Необходимо отметить, что в модели 4.2 для З необходимо дополнительно ввести условие " заинтересованности в успехе" (или " регулярности" ) – требование подобрать экономические параметры модели таким образом, чтобы обеспечить повышение его фактических доходов при снижении числа повторных запусков, т. е.:
где индексы соответствуют исходам " успех с первой попытки", " успех со второй попытки" и " неудача". Это достигается выполнением требования:
Область допустимых решений W ПЗС, следовательно, будет выше минимального уровня страховой ставки aMIN. Для второго активного субъекта – П введенное выше условие выполняется автоматически. Расчет минимально допустимой надежности PMIN может быть выполнен на множестве допустимых решений. С учетом сделанных предположений для данной модели максимальные потери могут составлять:
Максимальные возможные доходы участников выражаются величинами:
Модель 4.3. Повторная реализация вообще не предусматривается (в силу возможной уникальности условий и срока его проведения). В этом случае придем к следующей модели. П страхует свои затраты, сделанные им при оплате реализации. Как и прежде предполагается, что первоначальные выплаты равны: C – S Э. Именно возможность возврата этой суммы получает П при заключении договора страхования. При успешном выполнении проекта расходы П равны C, т. к. он выплачивает еще и прибыль S Э эксплуатирующей организации. В случае неудачи потерю затрат компенсирует С. Таким образом, ожидаемые средние доходы П составят:
Для З, соответственно:
Так как эксплуатирующая организация застраховала свою прибыль, то эта прибыль меньше, чем максимально возможная ( S Э ), но в то же время она гарантированно больше нуля, чему она равнялась бы при неуспешном выполнении проекта и отсутствии договора страхования.
Т.о. модель 4.3 задается уравнениями:
Рассмотрение минимальных экономических требований участников операции страхования одиночной реализации проекта позволяет выделить области допустимых решений для каждого из них при назначении страховых ставок. При этом для З риск невелик и ограничение на величину a З тривиально – a З < 1. Следовательно, область допустимых решений будет фактически определяться требованиями со стороны П и С, т.е. W ПЗС = W ПС, и выражаться результатом решения системы неравенств:
При условии принятия договорного уровня a З с использованием дополнительной информации, которой располагают договаривающиеся стороны, граничное значение вероятности успешной реализации будет определяться выражением:
Так, например, для случая относительно низкорентабельного проекта ( N П = 1, 2 ) при a З = 0, 1 и D Э = 0, 2 искомая величина вероятности составит 0, 9, что является весьма жестким требованием к З и П, учитывая необходимость наличия некоторого запаса по надежности для возможных уступок на переговорах с С. Повышая N П до уровня 1, 5, можно снизить нижний предел вероятности до значения PMIN = 0, 8. Модель 5. Модель этого типа соответствует случаю создания взаимного страхового фонда (ВСФ) П и З. Наличие такого фонда оправдано при проведении серии проектов. Предполагается, что ВСФ образуется при отсутствии предложения на рынке страховых услуг по компенсации потерь при реализации проекта и используется в целях распределения нагрузки между его учредителями. Страховые компании привлекаются только для компенсации потерь ожидаемой прибыли. Условия функционирования страхового фонда: v перед каждой реализацией проекта П и З вносят в фонд определенную сумму денег; v величина взноса определена как b -доля ( 0 < b < 1 ) разницы между установленным максимальным размером фонда ( Ф MAX ) и его текущим содержанием на момент перед очередной реализацией; v взносы между П и З распределены в пропорции:
где b П и b З – относительные объемы их долевого участия в ВСФ; v при неудачной реализацией П и З получают из фонда суммы, пропорциональные их взносам; v суммарная разовая выплата из фонда не может превышать величину CMAX; v объем программы фиксирован ( N – необходимое количество реализации проекта), задачей участников деятельности является ее полная реализация; ответственность за невыполнение отдельных этапов программы делится между участниками ВСФ – субъектами коммерческой деятельности; v в распоряжении участников реализации программы остается прибыль, полученная от использования принадлежащих им объектов страхования, оставшаяся после производства необходимых закупочных (арендных) выплат. В целях упрощения рассуждений не делается предположений относительно выплат из прибыли, последняя считается фиксированной и известной для каждого участника заранее и рассматривается как чистая прибыль. В модели рассмотрены математические ожидания накопленных значений доходов участников договора страхования, а также накопленного размера ВСФ. Объектом моделирования является пошаговый процесс выполнения программы. Каждый шаг включает предварительные страховые операции по формированию ВСФ и заключению договоров со страховыми компаниями, непосредственное осуществление программы, при необходимости компенсацию ущербов участников выполнения программы. Рекуррентное соотношение, определяющее в среднем динамику функционирования фонда, имеет вид:
где Ф i – текущий размер фонда на i -м шаге (после i -ой реализации); i – номер программы в застрахованной серии; D Фi – приращение размера фонда. В общем случае приращение D Фi представляется в виде суммы:
где D Фi , 0 =
Далее все аналитические выражения выводятся в предположении равенства Ф MAX и CMAX, что означает:
т.к. всегда
В зависимости от процедуры формирования ВСФ функция Модель 5.1 регулярных (обязательных) выплат в ВСФ. Выплаты в ВСФ производятся в обязательном порядке перед каждой реализацией в соответствии с установленными квотами ( b П и b З ). Тогда:
и выражение (11) для приращения ВСФ на i -м шаге примет вид:
а с учетом этого определится и рекуррентное выражение для описания динамики среднего размера ВСФ:
которое преобразуется к явному виду:
Средний размер однократных суммарных выплат из ВСФ на компенсацию ущерба при страховом случае определяется стационарным значением размера фонда:
Средний размер однократных суммарных взносов участников выполнения программы в ВСФ составляет:
где M [ ] – операция определения математического ожидания случайной величины. Уравнения для субъектов страхования описывают их ожидаемые доходы на i -м шаге. При успешной реализации (с вероятностью P ) П и З получают доходы S А и S Э, соответственно, а перед выполнением программы оплачивают стоимость страховой премии a П * S А и a З * S Э по согласованным со страховщиком индивидуальным тарифным ставкам a П и a З, а также делают взнос в ВСФ:
При неудачном выполнении программы страховщик выплачивает в порядке компенсации неполученной прибыли сумму S А в пользу П и S Э – З. Кроме того П и З должны получить из взаимного страхового фонда свою долю ( b П * Фi -1 и b З * Фi -1 соответственно); взнос в ВСФ при этом не делается. При этом предполагается, что всеми участниками страхового договора ведется честная игра и информация о фактическом исходе выполнения программы не является основанием для изменения правил осуществления выплат. В результате получаем:
Модель 5.2 сингулярных (условных) выплат в ВСФ. Предполагается, что на очередном шаге программы взносы в ВСФ выплачиваются только при условии удачного выполнения программы на предыдущем шаге. В этом случае:
и выражение для приращения ВСФ на i-м шаге примет вид:
С учетом (16) и (17) уравнение, описывающее динамику среднего размера фонда, задается выражением, в явном виде связывающим на каждом шаге выполнения программы искомую величину с максимальным размером ВСФ, основными характеристиками процессов формирования фонда и надежностью выполнения элемента (шага) программы,
Выражение (18) справедливо, начиная со 2-го шага программы. При этом считается, что Ф0= 0 и Ф1 = b * ФMAX. Стационарное значение размера фонда (средний размер однократных суммарных выплат) равно:
Средний размер однократных суммарных взносов участников выполнения программы в ВСФ в данном случае составляет:
Формулы (19) и (20) получены в предположении выполнения условия сходимости бесконечного ряда сумм (18):
Уравнения для субъектов страхования, как и в первом варианте Модели 5, описывают их ожидаемые доходы на i -м шаге. При успешном выполнеии программы расчеты производятся аналогично Модели 5.1. Однако, в случае неудачи взносы в совместный страховой фонд не делаются, а в дальнейшем накопление средств в Фонде производится заново. Остальные условия, в том числе и порядок отношений со страховщиком, остались без изменений. С учетом принятых во втором варианте изменений, получаем:
Уравнения (11), (14) полностью описывают Модель 5. Модель 6. Шестая модель может описывать целый подкласс реальных страховых договоров с тремя участниками. Рассмотрим частный случай. В данной модели предполагается наличие совместного страхового фонда, аналогичного рассмотренному в Модели 5, но отличающегося тем, что по условиям выполнения программы при потере объекта страхования вследствие его отказа виновная сторона (П или З) обязана провести повторную реализацию программы за свой счет. Субъекты П и З должны предусмотреть такой случай, формируя ВСФ. Однако, выплаты из ВСФ производятся только организатору повторного проекта.
Рис. 14. Замкнутая модель страхования Как и в моделях 5.1 и 5.2, в рассматриваемой модели нетто-ставки в договорах П Для описания динамики среднего объема страхового фонда по прежнему справедливы соотношения (9)...(14), (16)...(20). Из рассмотрения доходов участников при каждом возможном исходе находятся уравнения для Модели 6.1 регулярных выплат в ВСФ:
Аналогично находим уравнения для Модели 6.2 сингулярных выплат в ВСФ:
Разработанная совокупность моделей коллективного страхования крупных рисков является одной из попыток в отечественной практике страхования осмыслить с единых позиций вопрос эффективности в первую очередь экономических взаимоотношений между участниками страховой деятельности. В ходе исследования были сделаны важные для практики выводы о необходимости поиска согласованного оптимума страховой ставки при заключении договоров страхования, а также построения системы страхования с расчетом на длительную перспективу стабильных взаимоотношений. В этих условиях применение моделей коллективного страхования позволит проанализировать различные ситуации на формирующемся в России рынке страхования крупных рисков. В первую очередь здесь следует обратить внимание на вопросы экономической стабильности участников и формирование подходов к ценообразованию как в части оценивания рисков, так и предоставляемых услуг по обеспечению выполнения программ. Разумеется, представленная в отчете система моделей не является исчерпывающей. Однако, положенный в ее основу подход позволяет организовать наращивание с перспективой развития в автоматизированную экспертную систему поддержки управленческих решений в части страхования программ. |
Последнее изменение этой страницы: 2020-02-17; Просмотров: 174; Нарушение авторского права страницы