Резолюция в логике высказываний

⇐ ПредыдущаяСтр 30 из 32Следующая ⇒

Пусть А, В, С... - атомарные формулы логики высказываний. Формулу вида (AÚ BÚ...Ú D), где А, В, …, D - атомарные формулы, назовем дизъюнктом. Говорят, что два дизъюнкта С₁ и С₂ содержат контрарную пару литер X и , если они имеют следующее представление:

C₁ = RÚ...Ú X,

C₂ = QÚ...Ú .

Пусть, например С₁ = А Ú X и С₂ = В Ú .

Тогда дизъюнкт (АÚ В) является резолюцией дизъюнктов С₁ и С₂.

Лемма. Пусть С₁ и С₂ - два дизъюнкта и I - атомарная формула. Если IÎ C₁ и , то дизъюнкт (С₁\{I}) является логическим следствием дизъюнктов С₁ и С₂.

Доказательство. Пусть С_R - резольвента дизъюнктов С₁ и С₂.

Лемма утверждает, что C₁, C₂ ^|^¾ C_R, что равносильно тождественной истинности формулы C₁Ù C₂ ® C_R.

Последняя ложна, если С₁ Ù С₂ истинно и С_R ложно.

Пусть С₁ = С_R Ú I и C₂ = С_R Ú .

Имеем C₁ Ù C₂ = (C_R Ú I) Ù (C_R Ú ) = C_R.

Следовательно, в силу преобразований логики высказываний С₁ Ù C₂ эквивалентна С_R, а это значит что С₁Ù C₂®C_R тождественно истинная формула.

На основании метода резолюций устанавливается невыполнимость некоторого множества дизъюнктов. Пусть требуется доказать, что формула j выводима из формул e₁, e₂, ..., e_n, т.е. установить, что формула

e₁ Ù e₂ Ù...Ù e_n ® j (7.2)

тождественно истинна.

Это эквивалентно доказательству того, что формула

e₁ Ù e₂ Ù...Ù e_n Ù (7.3)

является тождественно ложной.

Обозначим через - логическую константу " ложь" (пустой дизъюнкт). Считается, что множество формул f₁, f₂, ..., f_t противоречиво (невыполнимо), если

f₁ Ù f₂ Ù...Ù f_t ® (7.4)

является тождественно истинной. Таким образом, если доказывается формула (7.3), то тем самым устанавливается невыполнимость множества формул f₁, f₂, ..., f_t.

Из всех этих рассуждений логически следует, что невыполнимость (7.3) эквивалентна выводимости из множества формул

e₁, e₂, ..., e_n,

пустого дизъюнкта. Очевидно, что пустой дизъюнкт () является резольвентой дизъюнктов С₁ = I и С₂ = , т.е. I, ^|^¾ .

В качестве примера установим невыполнимость множества дизъюнктов:

C₁ = p Ú q;

C₂ = p Ú r;

C₃ = Ú ;

C₄ = .

1. Резольвентой С₂ и С₄ является С₅ = r.

2. Резольвентой С₅ и С₃ является дизъюнкт С₆ =

3. Резольвентой С₆ и С₁ является дизъюнкт С₇ = p.

4. Резольвентой С₄ и С₇ является пустой дизъюнкт .

Существует несколько стратегий резолюционного вывода. Проблема выбора эффективной стратегии связана с уменьшением длины вывода или, в конечном итоге, сокращением числа лишних порожденных резольвент, которые не влияют на выводимость пустого дизъюнкта. Рассмотрим две основные стратегии порождения резольвент: линейную резолюцию и семантическую резолюцию.

Линейная резолюция в L

Определение. Для данного множества S дизъюнктов и дизъюнкта С₀ из S линейный вывод дизъюнкта С_n из S с верхним дизъюнктом С₀ - это вывод, изображенный на рис. 1, где

1) для i = 0, 1, ..., n-1 дизъюнкт C_i₊₁ есть резольвента дизъюнкта С_i и В_i; дизъюнкты C_i называется центральными В_i - боковыми.

2) В_i либо принадлежит S, либо есть С_j для некоторого j < i. Показано, что линейная резолюция является полной, т.е. для любого противоречивого множества дизъюнктов всегда выводится пустой дизъюнкт.

Дополнительное усиление рассмотренной стратегии предложено Лавлендом, Ковальским и Кюнером. Ими установлены условия, при которых центральный дизъюнкт позднее может участвовать в роли бокового дизъюнкта. Это свойство позволяет сократить число лишних дизъюнктов, поскольку становится ясно, будет или нет тот или иной центральный дизъюнкт использован для порождения пустого дизъюнкта. Прежде всего, множество литер произвольным образом упорядочивается, т.е. считается известным, какую литеру поставить левее в записи дизъюнкта, а какую правее. Например, пусть P > Q > R > тогда считаем, что дизъюнкт PÚ QÚ записан верно, а PÚ Ú Q - нет.

При порождении резольвент отсекаемая литера включается в представление резольвенты, но при этом указывается в рамке. Например, если

C₁ = P Ú Q

C₂ = Ú R,

то резольвента С₁ и С₂ имеет вид

P Ú Ú R.

Литеры в рамке служат для учета отрезанных литер: они не участвуют в дальнейшем порождении резольвент.

Рассмотрим дизъюнкт специального вида, в котором последняя литера не обрамлена и для этой последней литеры имеется контрарная обрамленная литера, например, Ú Ú .

Дизъюнкт такого типа называется редуцируемым. Если С - редуцируемый дизъюнкт, то его можно сократить за счет отбрасывания последней литеры, а также всех обрамленных литер, за которыми не следует необрамленной литеры. Для редуцируемого дизъюнкта Ú Ú это сразу дает .

Следующая лемма формализует введенные определения.

Лемма. Если в некотором выводе С является редуцируемым упорядоченным дизъюнктом, то существует центральный упорядоченный дизъюнкт C_j (j< 1), такой, что редукция С_i+1 дизъюнкта C_i является резольвентой С_i и С_j.

Доказательство. Если С_k и С_k+1, два соседних упорядоченных дизъюнкта на рис.7.1, то все литеры дизъюнкта С_k содержатся в С_k+1 (обрамленные литеры учитываются). Действительно, С_k+1 представляется как

Ú (C_k\{I}) Ú (B_k\ ),

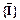где I - отсекаемая литера.

Пусть теперь С_i редуцируемый упорядоченный дизъюнкт, т.к. его последняя необрамленная литера, скажем, I контрарна некоторой обрамленной литере, то дизъюнкт С_i содержит некоторый центральный дизъюнкт P Ú , где Р - некоторая дизъюнкция литер. Но тогда резольвентой С_i и P Ú является С_i Ú P = C_i поскольку Р содержится в С.

С учетом доказанной леммы упорядоченный вывод (называемый OL - выводом ) определяется следующим образом:

1) Каждый дизъюнкт В_i либо принадлежит S, либо является ранее порожденным центральным дизъюнктом.

2) Если С_i редуцируемый упорядоченный дизъюнкт, то С_i+1 является результатом редукции С_i. В противном случае С_i+1 есть резольвента С_i и В_i, причем В_i принадлежит исходному множеству дизъюнктов и отсекаемая литера в С_i последняя.

3) В вывод не входят тавтологии.

Пример. Построим OL - вывод пустого дизъюнкта из множества дизъюнктов:

C₁ = P Ú Q,

C₂ = R Ú ,

C₃ = R Ú

C₄ = Ú

C₅ = Ú ;

P > Q > R >

1. Находим резольвенту дизъюнктов С₁ и С₂, для которых отсекаемая литера последняя

C₆ = P Ú Ú R.

2. Находим резольвенту дизъюнктов С₆ и С₄:

С₇ = P Ú Ú Ú .

3. Поскольку дизъюнкт С₇ редуцируем, то сразу находим

С₈ = Р

как результат редукции С₇.

4. Находим резольвенту дизъюнктов С₈ и С₃:

С₉ = Ú R.

5. Находим резольвенту С₉ и С₅:

C₁₀ = Ú Ú .

C₁₀ является редуцируемым дизъюнктом. Следовательно, его редукция сразу дает

C₁₁ = .

3.5.2.2 Метод линейного вывода в L Лавленда, Ковальского и Кюнера

Рассмотрим пример линейного вывода. Пусть дано

Введем дополнительные определения:

1. Входная резолюция – это применение правила резолюции, в котором одна из посылок – входной дизъюнкт (входная резолюция – это частный случай линейной резолюции).

2. Входным дизъюнктом является каждый член исходного множества S дизъюнктов.

3. Входной вывод – это вывод, в котором любое применение резолюции является входной резолюцией.

4. Входное опровержение – это входной вывод дизъюнкта ÿ из S.

5. Упорядоченный дизъюнкт – это последовательность различных литер. Это означает, что мы должны установить порядок всех литер в дизъюнкте. Примем соглашение, что литера L₂ меньше, чем литера L₁, в дизъюнкте С в точности тогда, когда L₂ следует за L₁ в последовательности, указанной в задании этого дизъюнкта. Таким образом, последняя литера всегда будет считаться наибольшей в дизъюнкте.

Уточним, что же предложили Лавленд, Ковальский и Кюнер.

Для этого рассмотрим пример. Здесь дизъюнкт p не является входным дизъюнктом. При этом легко видеть, что входное опровержение для исходного множества S отсутствует. Поэтому неизбежно использование одного из центральных дизъюнктов в качестве бокового. Однако, тогда возникает необходимость поиска необходимого и достаточного условия, при котором боковой дизъюнкт должен быть одним из ранее порожденных центральных дизъюнктов.

Так вот, информация об отрезаемых литерах, записанная надлежащим образом, а также использование упорядоченного дизъюнкта дают возможность определить это условие. Уточним один важный момент - о записи отрезаемых литер .

Пусть С₁ и С₂ следующие упорядоченные дизъюнкты:

Результатом резолюции этой пары будет упорядоченный дизъюнкт – (p Ú r). При этом литеры q и - контрарны, примем соглашение, что результат их дизъюнкции удалять не будем, а запишем его в виде одной левой литеры, обрамленной ее в рамку. Обрамленная литера – это отрезаемая литера, которая учитывается в дальнейших резолюциях следующим образом:

1. Обрамленную литеру должны выбрасывать только тогда, когда за ней не следует никакая необрамленная литера.

2. Если в упорядоченном дизъюнкте имеется более одного вхождение одной и той же необрамленной литеры, то всегда сохраняем самое левое вхождение, остальные совпадающие отбрасываем. Этот процесс называется отождествлением влево.

Перерисуем предыдущий пример

Здесь дизъюнкт p Ú q Ú - редуцируемый дизъюнкт, который сразу дает пустой дизъюнкт.

Это и есть необходимо и достаточное условие использования централизованного дизъюнкта в качестве бокового. В нашем случае это дизъюнкт р.

Применяя резолюцию дизъюнктов

Все литеры в результате обрамлена, т.е. за ними не следует необрамленная литера, поэтому мы их удаляем все, в результате получаем пустой дизъюнкт, т.е линейное опровержение. Порождаемые дизъюнкты типа называются редуцируемыми, их появление означает, что некоторый централизованный дизъюнкт нужно использовать в качестве бокового.

Пример:

Эффективная реализация

Условимся обозначать боковой дизъюнкт B_i сбоку от ребра C_i, тогда линейный вывод можно представить в виде дерева. Рассмотрим его на примере

Выберем в качестве C₀= p Ú q, тогда пригодные на первом шаге в качестве бокового – дизъюнкты и т.д.

Процесс закончен, так как порожден. Самая левая ветвь соответствует OL – опровержению.

Метод поиска в глубину

Определение:

cc) глубина дизъюнкта С₀ в OL - выводе с верхним укороченным дизъюнктом С₀ равна 0;

dd)если глубина некоторого укороченного дизъюнкта с равна k и R – есть укороченного результата дизъюнкции С с некоторым боковым дизъюнктом, то глубина дизъюнкта R равна k+1;

ee) длина доказательства (опровержения) с верхним дизъюнктом С₀ – это глубина пустого дизъюнкта.

Пусть d^* – заранее заданное пороговое число.

Описание метода:

1. Положить CLIST = (C₀)

2. Если CLIST пуст, закончим, не найдя доказательства, иначе на следующий шаг.

3. Пусть С – первый упорядоченный дизъюнкт в списке CLIST. Выбросим С из CLIST. Если глубина С > d^*, то на шаг 2, иначе на шаг 4.

4. Найдем все укор. дизъюнкты в S, которые могут быть боковыми дизъюнктами для С. Если таких боковых дизъюнктов нет, то на шаг 2. В противном случае построим результаты R₁, …, R_m дизъюнкта С с его боковыми дизъюнктами. Пусть R_i^* есть редукция дизъюнкта R_i, если R_i редуцируем. В противном случае положим R_i^*=R_i.

5. Если какой-либо из дизъюнктов R_q^* (1£ q£ m) пуст, то закончим, получив доказательство, иначе на следующий шаг.

6. Поместим R₁^*, …, R_m^* (в произвольном порядке) в начало списка CLIST и перейдем к шагу 2.

В методе поиска в глубину узел разворачивается полностью, если он вообще выбирается для развертывания, т.е. порождаются все возможные узлы-наследники.

Смэйгл и Нильсон модифицировали этот метод.

В модифицированном методе поиска в глубину в CLIST помещаются пары (С, В). В шестом шаге, если нет пары для R_i*, то эту резольвенту отбрасываем.

Эвристики поиска в дереве

Использование эвристики может привести к тому, что доказательство не будет найдено, хотя оно и существует. Однако она может значительно ускорить работу модифицированного метода поиска в глубину. В области доказательства имеется много эвристик. Обсудим некоторые из них:

А. Стратегия отбрасывания.

Говорят, что упорядоченный дизъюнкт С₁ поглощает другой упорядоченный дизъюнкт С₂, если дизъюнкт, состоящий из необрамленных литер в С₁, поглощает дизъюнкт, состоящий из необрамленных литер в С₂.

Упорядоченный дизъюнкт называется тавтологией, если он содержит контрарную пару необрамленных литер.

В модифицированном методе поиска в глубину в конце шага 4 нужно проверить, является ли R_i^*(i=1, …, m) тавтологией. Если R_i^* – тавтология, то отбрасываем его. Кроме того, следует отбросить R_i^*, если в CLIST имеется пара (С, В) такая, что R_i^* поглощается дизъюнктом С.

В. Стратегия предпочтения кратчайших дизъюнктов.

Эта стратегия вводит в модифицированный метод поиска в глубину упорядочение пар (С, В) в CLIST, чтобы лучшие пары стояли первыми. Оценивать пары рекомендуется по длине получаемого результата Length(R). Чем короче длина, тем лучше пара (С, В).

В действительности не надо вычислять R, чтобы найти ее длину, достаточно оценки: Length (R) £ Length (C) + Length (B) – 2. Смэйгл рекомендует упорядочивать пары (С, В) в списке CLIST по возрастанию.

С. Использование эвристических оценочных функций

Определим h^*(C, B) для пары (С, В), как число применений правила резолюции в минимальном доказательстве с верхним укор. дизъюнктом С и первым боковым дизъюнктом В.

Однако h^*(C, B) заранее неизвестна, поэтому введем оценку h(C, B) величины h^*(C, B). Предположим, что h(C, B) можно выразить в виде: h(C, B) = w₀+w₁f₁(C, B)+…+w_nf_n(C, B) (1), где f_i (i=1, …, n) – вещественная функция от С и В, а w_i – вес, сопоставленный величине f_i. (f_i называют характеристикой пары (С, В)).

Возможны следующие характеристики пар:

1. Число необрамленных литер в C.

2. Число обрамленных литер в С.

3. Число боковых дизъюнктов для С.

4. Число констант в последней литере из С.

5. Число функциональных символов в последней литере из С.

6. Число обрамленных литер в С, поглощающих последнюю литеру из В.

7. Число различных переменных в С и В.

8. length (C) + length (B) – 2

9. Число констант в С / (1+число переменных в С)

10. Число констант в С / (1+число различных переменных в С)

11. Глубина С.

12. Число необрамленных литер, входящих как в С, так и в В.

13. Число литер в В, имеющих обрамленное дополнение в С.

14. Число различных предикатных символов в С и В.

Функция h(C, B) может быть линейной или нелинейной от f₁(C, B), …, f_n(C, B), будем называть ее эвристической оценочной функцией, или просто оценочной функцией. Будем помещать пары (С, В) в CLIST по возрастанию значений h(C, B). Рассмотрим один из способов определения подходящих величин w₀, …, w_n.Способ определения значений множества w.

Допустим, что мы знаем величины h^*(C₁, B₁), …, h(C_q, B_q), тогда определение w₀, …, w_n таких, что минимально выражение (2) – оценка по наименьшим квадратам.

Определим матрицы H, F и W следующим образом:

Тогда W=(F’F)^–1F’H (3), где F’ – транспонированная матрица F, (F’F)^–1 – обратная матрица к (F’F).

Рассмотрим пример. Занумеруем все дизъюнкты дерева. Используем следующие характеристики.

f₁(C, B) = length (C) + length (B) – 2

f₂(C, B) = число обрамленных литер в С

f₃(C, B) = число необрамленных литер, входящих как в С, так и в В

f₄(C, B) = число литер в В, имеющих обрамленное дополнение в С

f₅(C, B) = число обрамленных литер в С, поглощающих последнюю литеру из В

Вычисляя характеристики для любой пары дерева, получим:

i	пара	f₁(C_i, B_i)	f₂(C_i, B_i)	f₃(C_i, B_i)	f₄(C_i, B_i)	f₅(C_i, B_i)	h(C_i, B_i)*
	(1, 2)
	(1, 3)
	(4, 6)
	(4, 7)
	(5, 8)
	(5, 9)
	(10, 14)
	(10, 15)
	(11, 16)
	(11, 17)
	(12, 18)
	(12, 19)
	(13, 20)
	(13, 21)

Вычисляя по (3) W, получим:

w₀=0, 3	w₂=0, 76	w₄=–1, 44
w₁=1, 68	w₃=–0, 24	w₅=0, 6

Тогда линейная оценочная функция примет вид:

h(C, B)=0, 30+1, 68f₁(C, B)+0, 76 f₂(C, B)–0, 24 f₃(C, B)–1, 44 f₄(C, B)+0, 6 f₅(C, B)

Если упорядочить пары в CLIST непосредственно перед 3 шагом модифицированного метода поиска в глубину, то получим 144 ветки дерева.

Конечно, чтобы оценочная функция была хорошей,

Но нас должен волновать вопрос и о том, необходимо рассмотреть как можно больше примеров.является ли выбранное множество характеристик хорошим?

Конечно, если оценочная функция обобщается на новые примеры, то можно считать это множество хорошим, в противном случае его надо менять.

Семантическая резолюция

Обратимся теперь к стратегии семантической резолюции, предложенной Слэйглом. Стратегия на основе семантической резолюции также использует упорядочение литер, как и OL -резолюция. Кроме того, эта стратегия основывается на разделении всего множества исходных и порождаемых дизъюнктов на два непересекающихся класса, назовем их Т и F. Такое разбиение возможно, если задать некоторую интерпретацию I для формул исходного множества. В интерпретации I часть дизъюнктов окажется истинной, а часть ложной. Множество истинных дизъюнктов в интерпретации I - это по определению множество Т; множество ложных дизъюнктов в интерпретации I - это по определению есть множество F.

При построении вывода требуется выполнение двух условий:

1) резольвента строится для дизъюнктов С₁ и С₂ таких, что С₁ Î T, а C₂ Î F

2) отсекаемая литера в дизъюнкте С₂ должна быть самой правой литерой.

Пусть E₁, E₂, ..., E_q некоторое множество дизъюнктов, принадлежащих F, а N - дизъюнкт из Т.

Тогда множество { E₁, E₂, ..., E_q, N } называется клашем, если выполняется следующее условие:

(i) R₁ = N;

(ii) i < 1, R_i₊₁ есть резольвента R_i_-1 и E_i_-1; отсекаемая литера - старшая в E_i (самая правая);

(iii) R_q₊₁ Î F.

R_q₊₁ называется резольвентой данного клаша.

Пример. Пусть

C₁ = R Ú Ú ,

C₂ = P Ú R,

C₃ = Q Ú R,

C₄ = ,

P > Q > R >

Пусть в интерпретации I R - ложен, Р - ложен, Q - ложен. Тогда клашами являются множества

K₁ = {С₃, C₄},

K₂ = {C₂, C₄}.

Вывод на основе семантической резолюции строится так, что каждый дизъюнкт либо принадлежит исходному множеству дизъюнктов, либо является резольвентой некоторого клаша.

Так резольвентой С₅ клаша К₁ является Q; резольвентой С₆ клаша К₂ является Р.

Резольвентой С₅ и С₁ является дизъюнкт C₇ = R Ú .

Резольвентой С₇ и С₆ является дизъюнкт С₈ = R.

Резольвентой дизъюнктов С₈ и С₄ является .

Резолюция в PL

Применению OL-вывода в PL предшествует подготовительный этап, предложенный Девисом и Патнемом. Он включает в себя 3 стадии:

1) преобразование формулы в ПНФ;

2) преобразование матрицы в КНФ;

3) преобразование формулы в ССФ.

С реализацией второй стадии вы хорошо знакомы, поэтому рассмотрим 1-ю и 3-ю стадии.

В L имеются две нормальные формы: ДНФ и КНФ, в PL роль нормальной формы играет ПНФ – предваренная нормальная форма.

Определение: Говорят, что формула F в PL находится в ПНФ тогда и только тогда, когда формула F имеет вид: (Q₁x₁)…(Q_nx_n)(M), где (Q_ix_i) (i=1, …, n) есть либо (" x_i), либо ($x_i) и М есть формула, не содержащая кванторов.

(Q₁x₁)…(Q_nx_n) называется префиксом формулы F, М – матрицей формулы F.

Для преобразования формулы F в ПНФ используются законы эквивалентных преобразований, называемых законами принесения кванторов через Ù и Ú:

(1а) (Qx)F(x)Ú G=(Qx)(F(x)Ú G)

(1б) (Qx)F(x)Ù G=(Qx)(F(x)Ù G)

(2а) Ø ((" x)F(x))=($x)(Ø F(x))

(2б) Ø (($x)F(x))=(" x)(Ø F(x))

(3а) (" x)F(x)Ù (" x)M(x)=(" x)( F(x)Ù M(x))

(3б) ($x)F(x)Ù ($x)M(x)=($ x)( F(x)Ù M(x))

Однако " и $ нельзя проносить через Ú и Ù соответственно. В подобных случаях нужно поступать специальным образом. Т.к. каждая связанная переменная в формуле может рассматриваться лишь как место для подстановки какой угодно переменной, то каждую связанную переменную х можно переименовать в z и формула (" x)M(x) перейдет в (" z)M(z), т.е. (" x)M(x)= (" z)M(z). Предположим, что мы выбираем переменную z, которая не встречается в F(x). Тогда (" x)F(x)Ú (" x)M(x)= (" x)F(x)Ú (" z)M(z) путем замены всех х, входящих в (" x)M(x) на z, тогда согласно (1а):

(4а) (" x)F(x)Ú (" x)M(x)= (" x)(" z)(F(x)Ú M(z))

(4б) ($x)F(x)Ú ($x)M(x)= ($x)($z)(F(x)Ú M(z)).

Преобразование формул в ПНФ:

1) используем законы, чтобы исключить логические связки ~ и É

(5) F~G=(FÉ G)Ù (GÉ F)

(6) FÉ G=Ø FÚ G

2) используем законы, чтобы пронести знак отрицания внутрь формулы

(7) Ø (Ø F)=F

(8) Ø (FÚ G)=Ø FÙ Ø G

(9) Ø (FÙ G)=Ø FÚ Ø G

(10) Ø ((" x)F(x))=($x)(Ø F(x))

(11) Ø (($x)F(x))=(" x)(Ø F(x))

3) переименовываем связанные переменные, если это необходимо

4) используем законы (1а–4б), чтобы вынести кванторы в самое начало формулы для получения формулы, находящейся в ПНФ.

Пример 1: приведем формулу (" x)P(x)É ($x)Q(x).

(" x)P(x)É ($x)Q(x)=

=Ø ((" x)P(x))Ú ($x)Q(x)= по (6)

=($x)(Ø P(x))Ú ($x)Q(x)= по (2а)

=($x)(Ø P(x)Ú Q(x)) по (3б)

где ($x) – префикс, а (Ø P(x)Ú Q(x)) – матрица.

Пример 2: получить ПНФ для формулы:

(" x)(" y)(($z)P(x, z)Ù P(y, z))É ($u)Q(x, y, u))=

= (" x)(" y)(Ø (($z)P(x, z)Ù P(y, z)))Ú ($u)Q(x, y, u))= по (6)

= (" x)(" y)(" z)(Ø P(x, z)Ù Ø P(y, z))Ú ($u)Q(x, y, u))= по (2б) и (9)

= (" x)(" y)(" z)($u)(Ø P(x, z)Ù Ø P(y, z))Ú Q(x, y, u)) по (1а)

где (" x)(" y)(" z)($u) – префикс, а (Ø P(x, z)Ù Ø P(y, z))Ú Q(x, y, u)) – матрица.

Рассмотрим вопрос преобразования формулы F в скулемовскую стандартную форму (ССФ).

Для этого мы должны, сохраняя противоречивость формулы, элиминировать в ней кванторы существования путем использования скулемовских функций.

Условимся, что формула F находится в ПНФ:

(Q₁x₁)…(Q_nx_n)M, где М в свою очередь находится в КНФ, тогда:

1) выберем самый левый квантор существования Q_r в префиксе (Q₁x₁)…(Q_nx_n) (1£ r£ n);

2) если никакой " не стоит в префиксе левее Q_r, то выберем новую константу С, отличную от других констант, входящих в М, заменим все х_r, встречающиеся в М, на С и вычеркнем (Q_rx_r) из префикса;

3) Если Q_s₁, …, Q_sm – список всех ", стоящих левее Q_r, (1£ S₁< S₂< …< S_m< r), то выберем новый m-местный функциональный символ f, отличный от других функциональных символов, заменим все x_r в M на f(x_s₁, …, x_sm) и вычеркнем (Q_r, x_r) из префикса;

4) Весь этот процесс применим для всех $ в префиксе, двигаясь слева направо (следует отметить, что порядок выбора $ из префикса несущественен).

Последняя из полученных формул и есть ССФ формулы F (или просто стандартная форма формулы F). Константы и функции, используемые для замены переменных $, называются скулемовскими функциями.

Пример 1: получить стандартную форму формулы ($x)(" y)(" z)($u)(" v)($w) P(x, y, z, u, v, w).

В этой формуле левее ($x) нет ни одного ", значит заменяем х на а.

($u) находится (" y)(" z), значит заменяем u на f(y, z)

($w) находится (" y)(" z)(" v), значит заменяем w на g(y, z, v).

Тогда (" y)(" z)(" v)P(a, y, z, f(y, z), v, g(y, z, v)) – стандартная форма.

При использовании процедур опровержения не происходит потери общности, поэтому при доказательстве кванторы общности можно опустить.

Рассмотрим теперь непосредственно метод резолюций, применяемый в PL при построении OL-вывода.

Как и в L здесь существенным является нахождение в дизъюнкте литеры, которая контрарна литере в другом дизъюнкте. Рассмотрим дизъюнкты: С₁: P(x)Ú Q(x) и C₂: Ø P(f(x))Ú R(x).

С первого взгляда в С₁ нет литеры, контрарной какой-либо литере в С₂, однако если подставить f(0) вместо x в С₁ и a вместо x в C₂, то получим: С₁’: P(f(a))Ú Q(f(a)) и C₂’: Ø P(f(a))Ú R(a).

C₁’ и C₂’ называются основными примерами С₁ и С₂ соответственно, а P(f(a)) и Ø P(f(a)) контрарны друг другу. Следовательно, из C₁’ и C₂’ можно получить резольвенту:

C₃’: Q(f(a))Ú R(a).

В общем случае, подставив f(x) вместо x в C₁, получим: C₁^*: P(f(x))Ú Q(f(x)). Снова С₁^* есть пример С₁. Литера P(f(x)) из С₁^* контрарна литере Ø P(f(x)), тогда резольвента С₁^* и С₂:

С₃: Q(f(x))Ú R(x).

При этом С₃’ является примером С₃. Кроме того, дизъюнкт С₃ является наибольшим общим дизъюнктом в том смысле, что все другие дизъюнкты, порожденные подобным образом, есть приме

С₃ будем называть резольвентой С₁ и С₂. Таким образом, получение резольвенты из двух дизъюнктов в PL связано с подстановкой.

Определение: Подстановка – это конечное множество вида {t₁/v₁, …, t_n/v_n}, где каждая v_i – переменная, а t_i – терм, отличный от v_i, при этом все v_i различны. Если t₁, …, t_n – основные термы, то подстановка называется основной. Подстановка, которая не содержит элементов, называется пустой и обозначается e. Будем использовать греческие буквы для обозначения подстановки.

Определение: Пусть q ={t₁/v₁, …, t_n/v_n} – подстановка и Е – выражение. Тогда Еq – выражение, полученное из Е заменой одновременно всех вхождений переменной v_i (1£ i£ n) в Е на t_i. Еq называют примером Е.

Определение: Пусть q ={t₁/x₁, …, t_n/x_n} и l={u₁/y₁, …, u_m/y_m} – две подстановки. Тогда композиция q·l есть подстановка, которая получается из множества {t₁/x₁, …, t_n/x_n, u₁/y₁, …, u_m/y_m} вычеркиванием всех элементов t_jl/x_j, для которых t_jl = x_j, и всех элементов u_i/y_i, таких что y_iÎ {x₁, …, x_n}.

Пример: q ={t₁/x₁, t₂/x₂}={f(y)/x, z/y}

l ={u₁/y₁, u₂/y₂, u₃/y₃}={a/x, b/y, y/z}, тогда

q·l={t₁/x₁, t₂/x₂, u₁/y₁, u₂/y₂, u₃/y₃}={ f(y)/x, z/y, a/x, b/y, y/z}

Так как t₂l=x₂, а именно z/y, то этот элемент вычеркивается из множества y₁ и y₂Î {x₁, x₂, x₃}, т.е. a/x и b/y должны быть тоже вычеркнуты. Таким образом, получаем: q·l={f(b)/x, y/z}.

Композиция подстановок ассоциативна, а пустая подстановка e есть одновременно и левое и правое тождество, т.е. (q·l)·m=q·(l·m) и e·q=q·e для всех m, q, l.

⇐ Предыдущая 23 24 25 26 27 28 293031 32 Следующая ⇒