Коническо-цилиндрические редукторы

 

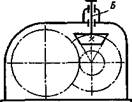
В двухступенчатых коническо-цилиндрических редукторах (рис. 2.11 —2.13) коническая пара может иметь прямые, косые или криволинейные зубья. Цилиндрическая пара также может быть либо прямозубой, либо косозубой.

Наиболее употребительный диапазон передаточных чисел для таких редукторов u = 8 ¸ 15. Наибольшие значения при прямозубых конических колесах u_max = 22; при конических колесах с круговыми зубьями u_max = 34.

 

 

Рис. 2.11. Двухступенчатый горизонтальный коническо-цилиндрический редуктор: а — кинематическая схема; б – обший вид редуктора с литым корпу­сом; в — общий вид редуктора со сварным корпусом

 

 

Рис. 2.12. Двухступенчатый коническо-цилиндрический редуктор с вертикальным тихоходным валом: а – кинематическая схема; б – общий вид

		Рис. 2.13. Кинематическая схема двухступенчатого коническо-цилиндрического редуктора с вертикальным быстроходным валом

 

 

Червячные редукторы

 

Червячные редукторы применяют для передачи движения между валами, оси которых перекрещиваются.

По относительному положению червяка и червячного колеса различают три основные схемы червячных редукторов: с нижним, верхним и боковым расположением червяка (рис. 2.14 — 2.16).

Искусственный обдув ребристых корпусов обеспечивает более благоприятный тепловой режим работы редуктора (рис. 2.14, в и г).

Выход вала колеса редуктора с боковым расположением червяка в зависимости от назначения и компоновки привода может быть сделан вверх (рис. 2.16, а) или вниз (рис. 2.16, б и в).

При нижнем расположении червяка условия смазывания зацепления лучше, при верхнем хуже, но меньше вероятность попадания в зацепление металлических частиц — продуктов износа.

Выбор схемы редуктора обычно обусловлен удобством компоновки привода в целом: при окружных скоростях чер­вяка до 4 —6 м/с предпочтительно нижнее расположение червяка; при больших скоростях возрастают потери на перемешивание масла, и в этом случае следует располагать червяк над колесом. В редукторах с верхним расположением червяка при включении движение

Рис. 2.14. Червячный редуктор с нижним расположением червяка: а — кинематическая схема; 6 — об­щий вид редуктора с разъемным корпусом; в — общий вид редуктора с ребристым разъемным корпусом и искусственным обдувом; г — то же, со снятой крышкой; д — общий вид редуктора с неразъемным корпу­сом

 

 

 

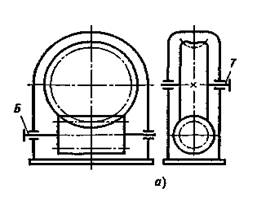
Рис. 2.15. Червячный редуктор с верхним расположением червяка:

а – кинематическая схема: б — общий вид редуктора с разьемным корпусом;

в — общий вид редуктора с неразъемным корпусом

 

обычно начинается при недостаточной смазке (за время остановки при редких включениях масло успевает стечь с зубьев колеса).

Передаточные числа червячных редукторов обычно ко­леблются в пределах и = 8 ¸ 80 (см. ГОСТ 2144-76).

Так как КПД червячных редукторов невысок, то для передачи больших

мощностей и в установках, работающих непрерывно, проектировать их нецелесообразно. Практически червячные редукторы применяют для передачи мощности, как правило, до 45 кВт и в виде исключения до 150 кВт.

Рис. 2.16. Червячный редуктор с вертикальным валом червячного колеса:

а - кинематическая схема; б - общий вид редуктора с разъемным корпусом;

в -общий вид редуктора с неразъемным корпусом

Зубчато-червячные, червячно-зубчатые

И двухступенчатые червячные редукторы

 

Схемы и общий вид зубчато-червячных и двухступенчатых червячных редукторов показаны на рис. 2.17 и 2.18. Передаточные числа зубчато-червяч-

 

Рис. 2.17. Двухступенчатый зубчато-червячный редуктор:

а – кинематическая схема; б – общий вид

 

 

Рис. 2.18. Двухступенчатый червячный редуктор:

а — кинематическая схема; б и в – варианты общею вида

ных редукторов u £ 150, а в от­дельных случаях и выше (для учебного проектирования реко­мендуется ограничиться и = 35 ¸ 80).

Двухступенчатые червячные редукторы изготовляют с пере­даточными числами и = 120 ¸ 2500 (при учебном проектиро­вании рекомендуется ограничиться и = 120 ¸ 400).

Планетарные и волновые редукторы

 

На рис. 2.19, а показана простая — с одной степенью сво­боды — планетарная передача, состоящая из солнечного коле­са 1, сателлитов 2 и корончатого колеса 3, неподвижно закрепленного в корпусе. Сателлиты совершают сложное

 

Рис. 2.19. Одноступенчатый планетарный редуктор: а - кинематическая схема; б – общий вид

 

движение: они обкатываются вокруг сол­нечного колеса и вращаются внутри неподвижного коронча­того колеса (некоторая аналогия с движением планет дала назва­ние этим передачам). Оси сател­литов установлены в водиле 4, геометрическая ось которого совпадает с геометрическими осями центральных колес — сол­нечного и корончатого. Чаще других встречаются передачи с числом сателлитов n_с = 3.

Рис. 2.20.Кинематическая схема двухступенчатого планетарного редуктора

Планетарные передачи ком­пактнее обычных зубчатых, так как при п_с сателлитах вращаю­щий момент передается не одним, а несколькими потоками;

в расчетах на прочность обычно принимают приведен-

ное число сателлитов n_c = n_с — 0, 7.

Для выравнивания нагрузки по потокам при нескольких сателлитах одно из центральных колес устанавливают без опор, т. е. выполняют плавающим в радиальном направлении. На рис. 2.19, б показан редуктор с плавающим (самоустанав­ливающимся) солнечным колесом. Для соединения плавающего солнечного колеса с валом применена зубчатая муфта с двумя зубчатыми сочленениями.

При последовательном соединении нескольких простых планетарных передач можно получить редуктор с большим пере­даточным отношением (рис. 2.20).

Волновые передачи можно рассматривать как разновид­ность планетарных передач, имеющих гибкое промежуточное колесо, деформируемое при передаче вращающего момента.

На рис. 2.21, а показана кинематическая схема волновой передачи: входной вал 1 приводит во вращение генератор волн 2, который представляет собой водило с двумя ролика­ми; гибкое колесо 3 выполнено в виде тонкостенного стакана, на утолщенной части которого нарезаны зубья, входящие в зацепление с внутренними зубьями неподвижного жесткого колеса 4; выходной вал 5 соединен с основанием тонкостен­ного стакана.

Генератор деформирует гибкое зубчатое колесо в радиаль­ном направлении, придавая ему форму эллипса, и вводит в зацепление зубья деталей 3 и 4 на полную рабочую высоту.

При вращении генератора зацепление зубьев перемещается подобно бегущей волне, что и дало название этим переда­чам.

Широкое распространение получили кулачковые генераторы волн (рис. 2.21, б). На профилированный кулачок А насажено внутреннее кольцо гибкого подшипника Б. Наружное кольцо гибкого подшипника сопряжено с внутренней поверхностью гибкого колеса В, обеспечивая ему заданную форму дефор­мации. Кольца гибкого подшипника имеют малую толщину и поэтому сравнительно легко деформируются. Ниже приведены для сравнения размеры двух подшипников с одним и тем же внутренним диаметром: гибкого и обычного шарикового ради­ального легкой серии:

 

 

Модули зубчатых колес 3 и 4 (см. рис. 2.21, а) одинаковы, но числа зубьев

	z3 u = ____________. z4 – z3

разные: z₃ < z₄. Передаточное число волновой передачи равно

 

 

 

Рис. 2.21. Волновой зубчатый одноступенчатый редуктор:

а — кинематическая схема; б — генератор волн: в — продольный разрез

 

При оптимальных значениях (z₄ - z₃) = 2 или 1 диапазон передаточных отношений в односту­пенчатых волновых редукторах составляет от 80 до 300 (и более). Волновые передачи обладают высокой нагрузочной способностью благодаря многопарности зацепления: одновременно в зацеплении может находиться до 25-30% пар зубьев.

На рис. 2.21, в показан волновой редуктор с кулачковым генератором волн 2 и гибким тонкостенным колесом 3 сварной конструкции. На ведущем валу 1 находится кулачок, на котором установлен гибкий подшипник, сопряженный с гибким колесом, зубья которого в двух зонах входят в зацепление с зубьями жесткого колеса 4. Кулачок генератора волн находится на валу с радиальным зазором; передача движения осуществляется зубчатой муфтой, которая обеспечивает самоустановку генера­тора при работе редуктора. С гибкого колеса вращающий мо­мент передается шлицами ведомому валу 5.

Мотор-редукторы

 

Мотор-редуктор — это агрегат, совмещающий в одном кор­пусе электродвигатель и редуктор. Последнее обстоятельство позволяет добиваться большой точности расположения вала редуктора относительно вала электродвигателя и уменьшает число деталей привода.

Чаще встречаются мотор-редукторы с зубчатыми переда­чами обыкновенными и планетарными.

 

Рис. 2.22. Мотор-редукторы: а – горизонтальный; б – вертикальный

 

Рис. 2.23. Мотор-редуктор с одноступенчатой зубчатой цилиндрической передачей

 

 

На рис. 2.22 показаны общие виды мотор-редукторов. На рис. 2.23 изображен в разрезе горизонтальный мотор-редуктор с одноступенчатой зубчатой цилиндрической передачей. Пока­занный на рис. 2.22, б вертикальный мотор-редуктор имеет две ступени: первую — зубчатую цилиндрическую обыкновенную и вторую — планетарную.

 

 

ГЛАВА III

ЗУБЧАТЫЕ ПЕРЕДАЧИ

ОБЩИЕ СВЕДЕНИЯ

 

Различают два вида зубчатых передач - закрытые и откры­тые. Эти передачи обычно разрабатывают в курсовых проектах учащиеся техникумов.

Закрытые, заключенные в отдельный корпус (например, редукторного типа) или встроенные в машину. Проектировочный расчет их выполняют на выносливость по контактным напря­жениям во избежание усталостного выкрашивания рабочих поверхностей зубьев. Определив на основе этого расчета размеры колес и параметры зацепления, выполняют затем про­верочный расчет на выносливость зубьев по напряжениям изгиба для предотвращения усталостного разрушения зубьев; обычно напряжения изгиба в зубьях, рассчитанных на контакт­ную прочность, оказываются ниже допускаемых. Однако при выборе слишком большого суммарного числа зубьев колес (более 200) или применении термохимической обработки поверх­ностей зубьев до высокой твердости (HRC> 45) может возник­нуть опасность излома зубьев. Для предотвращения этого раз­меры зубьев следует определять из расчета их на выносливость по напряжениям изгиба.

Открытые зубчатые передачи рассчитывают на выносливость по напряжениям изгиба с учетом износа зубьев в процессе эксплуатации. В этом случае нет необходимости проверять выносливость поверхностей зубьев по контактным напряжениям, так как абразивный износ поверхностей зубьев предотвращает выкрашивание их от переменных контакт­ных напряжений.

Зубчатые передачи, работающие с большими кратковремен­ными (пиковыми) перегрузками, необходимо проверять на от­сутствие опасности хрупкого разрушения или пластических деформаций рабочих поверхностей зубьев от контактных напряжений, а также на отсутствие хрупкого излома или пласти­ческих деформаций при изгибе. Это относится равно как к закры­тым, так и открытым передачам.

 

 

Рис. 3.1. Контактные напряжения в зоне соприкосновения цилиндров вдоль образующей

Кратковременное действие пиковых нагрузок не оказывает влияния на поверхностную и общую усталостную прочность зубьев. Поэтому определение напряжений, вызываемых такими нагрузками, следует рассматривать как проверку зубьев на по­верхностную и общую статическую прочность. Расчетные формулы имеют тот же вид, что и формулы для расчетов на усталостную прочность, но значения допускаемых напряжений, принимаемых в этих расчетах, различны.

Расчет закрытых зубчатых передач на выносливость рабо­чих поверхностей зубьев по контактным напряжениям основан на формуле Герца. Эта формула служит для определения макси­мального нормального напряжения в точках средней линии контактной полоски в зоне соприкосновения двух круговых цилиндров с параллельными образующими (рис. 3.1). При выводе формулы были приняты допущения: материал цилиндров идеально упругий, в точках контакта он находится в условиях объемного напряженного состояния — трехосного сжатия; наибольшее (по модулю) напряжение сжатия — главное напря­жение s₃ — принято обозначать s_mах; при эллиптическом за­коне распределения давления по ширине площадки контакта

 

(3.1)

где q – нагрузка на едницу длины контактной линии; с – ширина контактной площадки, определяемая из выражения

 

 

Подставив это значение в формулу (3.1.), получим

 

(3.2)

1 1 1 1

Здесь ^______ - приведенная кривизна цилиндров, ^______ = ^______ + ^______, где r₁ и

r_пр r_пр r₁ r₂

r₁ r₂

r₂ – радисы цилиндров; отсюда - r_пр = ^_________ ; v – коэффициент Пуассона, при-

r₁ + r₂

нятый равным 0, 3; Е – модуль упругости материала цилиндров; если цилиндры изготовлены из разных материалов, то определяют приведенный модуль упругости

 

§ 3.2. РАСЧЕТ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС НА КОНТАКТНУЮ ВЫНОСЛИВОСТЬ

 

Для расчета передач с цилиндрическими зубчатыми коле­сами (рис. 3.2) на выносливость рабочих поверхностей зубьев по контактным напряжениям пользу­ются формулой (3.2); максималь­ное нормальное напряжение s_тax принято обозначать s_н; индекс H (лат.) соответствует первой букве фамилии знаменитого физика Hertz'a; нагрузка на единицу дли­ны контактной линии зубьев

 

где нормальная сила в зацеплении;

Рис. 3.2. Геометрия зубчатого эвольвентного зацепления

Ft

- окружная сила; a_w – угол зацепления; по ГОСТ 13755-81 он принят равным 20^о*; b - угол наклона зуба по отношению к образующей делитель-ного цилиндра; К_н — коэффициент, учитывающий ди-

намиче­скую нагрузку и неравномерность распределения

нагрузки между зубьями и по ширине венца; b — шири-

на венца; k_e - коэф­фициент степени перекрытия.

Приведенный радиус цилиндров r_пр следует заменить величи­ной приведенного радиуса эвольвентных профилей зубьев в полюсе зацепления; так как

 

то

 

Подстановка приведенных значений величин в формулу (3.2) дает возможность выразить зависимость s_н от параметров зубчатой передачи в виде

 

(3.3)

 

Дальнейшие расчеты даны в соответствии с рекоменда­циями ГОСТ 21354-75. Допущенные в отдельных случаях незначительные отступления, практически не влияющие на величину конечного результата, имеют целью некоторое упро­щение расчета.

* В дальнейшем будем считать a_w » a, где a - делительный угол профиля или угол профиля исходного контура

 

Для практических расчетов по ГОСТ 21354-75 введены сле­дующие условные обозначения:

— коэффициент, учитывающий механиче­ские свойства материала сопряженных зубчатых колес; его раз­мерность соответствует размерности Ö E;

– безразмерный коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления;

— безразмерный коэффициент, учитывающий сум­марную длину

контактных линий; для прямозубых колес k_e = ^__________; для косозубых и шев-

4 - e_a

ронных k_e = e_a, где e_a - степень перекрытия.

С этими обозначениями формула (3.3) примет вид

 

(3.4)

 

Все величины, входящие в эту формулу, должны быть выра­жены в соответствующих единицах. В ГОСТ 21354-75 допу­щено отклонение от этого правила: момент выражен в Н × м, a d и b в мм, напряжение и модуль упругости в МПа (числен­но соответствует МН/м²).

В дальнейшем, следуя правилу теории размерностей, будем выражать момент в Н × мм, d и b в мм, s_н и Е в МПа (что численно соответствует Н/мм²).

Для стали принимают: Е = 2, 15 × 10⁵ МПа; коэффициент Пуассона v = 0, 3. При этих значениях коэффициент

 

 

Численные значения коэффициента Z_H:

для прямозубых колес при a = 20°, b = 0 Z_H = 1, 76;

для косозубых колес при a = 20°, b = 8¸ 15° Z_H = 1, 74¸ 1, 71;

для шевронных колес Z_H = 1, 57.

Средние значения коэффициента Z_e:

для прямозубых передач при a = 20° Z_e = 0, 9;

для косозубых передач Z_e = 0, 8.

После подстановки указанных значений коэффициентов в формулу (3.4) и замены в ней d₂ через межосевое расстояние a_w

 

получим формулы для проверочного расчета:

прямозубых передач

(3.5)

 

косозубых передач

 

(3.6)

 

Выражая в этих формулах величину b через a_w с помощью коэффициента

 

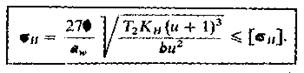
ширины зубчатого венца получим формулу для проектировочного расчета a_w, мм

 

(3.7)

 

Дляпрямозубых передач К_а = 49, 5; для косозубых и шев­ронных передач К_а = 43, 0.

Коэффициент К_H = К_Нa, К_НbК_Hv, где К_Ha — коэффициент, учи­тывающий неравномерность распределения нагрузки между зубьями; для прямозубых колес принимают K_Ha = 1, 0; для косозубых колес в зависимости от окружной скорости v: при v =10¸ 20 м/с и 7-й степени точности К_Нa — 1, 0¸ 1, 1, при v до 10 м/с и 8-й степени точности K_Ha = 1, 05¸ 1, 15; К_Нb — коэф­фициент, учитывающий неравномерность распределения нагруз­ки по ширине венца. При проектировании закрытых зубчатых передач редукторного типа принимают значения K_Hb по табл. 3.1.

3.1. Ориентировочные значения коэффициента K_Hb для зубчатых передач редукторов, работающих при переменной нагрузке

 

Расположение зубчатых колес относительно опор	Твердость НВ поверхностей зубьев
£ 350	> 350
Симметричное Несимметричное Консольное	1, 00-1, 15 1, 10-1.25 1, 20-1, 35	1, 05-1, 25 1, 15-1, 35 1, 25-1, 45
Меньшие значения принимают для передач с отношением ybd = b/d1 = 0, 4: при увеличении ybd до 0, 6 для консольно расположенных колес и ybd до 0, 8 при несимметричном расположении их следует прини­мать большие из указанных в таблице значений KHb. При постоянной нагрузке KHb = 1. Определение ybd см. формулу (3.8).

Динамический коэффициент K_Hvопределяют в зависимости от окружной скорости v колес и степени точности их изготов­ления.

Для прямозубых колес при v до 5 м/с следует назначать 8-ю степень точности по ГОСТ 1643-81; при этом K_Hv = 1, 05¸ 1, 10.

Для косозубых колес при v до 10 м/с назначают также 8-ю степень точности и принимают K_Hv= 1, 0¸ 1, 05. При v свыше 10 до 20 м/с и 7-й степени точности К_Hv. = 1, 05¸ 1, 1. Меньшие из указанных значений относятся к колесам с твердостью поверх­ностей зубьев НВ £ 350, большие - при твердости НВ > 350.

Коэффициенты К_Ha и K_Hvмогут быть определены только тогда, когда известны размеры передачи (надо знать скорость v). Поэтому при проектировочных расчетах по формуле (3.7) пред­варительно используют один коэффициент K_Hb, учитывающий неравномерность распределения нагрузки по ширине венца (см. табл. 3.1 ).

При проектировании редукторов обычно задаются величиной y_ba = b / a; для прямозубых передач принимают y_ba = 0, 125¸ 0, 25; для косозубых y_ba = 0, 25¸ 0, 40; для шевронных y_ba = 0, 5¸ 1, 0. Чтобы вычислить y_bd по выбранному

 

значению y_ba следует воспользоваться равенством; тогда

 

(3.8)

 

Допускаемое контактное напряжение определяют при проек­тировочном расчете по формуле

 

(3.9)

 

Здесь s_{H lim b}, — предел контактной выносливости при базовом числе циклов (значения s_{H lim b}, указаны в табл. 3.2); К_HL — коэффи­циент долговечности; если число циклов нагружения каждого зуба колеса больше базового, то принимают K_HL = 1. Именно такой случай типичен для курсовых проектов, выполняемых в техникумах.

В других условиях, когда эквивалентное число циклов перемены напряжений N_HE меньше базового N_HO, то

 

 

Если при расчете колес из нормализованной или улучшен­ной стали К_HL получается больше 2, 6, то принимают К_HL = 2, 6; для колес из закаленной стали К_HL £ 1, 8; [S_H] - коэффициент безопасности; для колес из нормализованной и улучшенной стали, а также при объемной закалке принимают [S_H] = 1, 1¸ 1, 2; при поверхностном упрочнении зубьев [S_H ] = 1, 2¸ 1, 3.

Данные для выбора материалов шестерни и колеса приве­дены в табл. 3.3. Рекомендуется назначать для шестерни и колеса сталь одной и той же марки, но обеспечивать соответст­вующей термической обработкой твердость поверхности зубьев шестерни на 20—30 единиц Бринелля выше, чем колеса.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Популярное:

1. Газовые редукторы-испарители
2. Одноступенчатые конические редукторы