КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ

Галкин А.Ф.

Г16 Лекции по физике: В 4 ч. Ч. 1. Механика / Владим. гос. ун-т. Владимир, 2004. 68 с.

ISBN 5-89368-473-7

Содержат шесть лекций, посвященных раскрытию физического смысла основных законов и понятий физики, а также примеры и вопросы для самоконтроля.

Предназначены для студентов технических специальностей всех форм обучения вузов, а также преподавателей.

Ил. 42. Библиогр.: 8 назв.

УДК 53(07)

ISBN 5-89368-473-7 Ó Владимирский государственный

университет, 2004

Введение

" Физика – наука, изучающая общие свойства и законы движения вещества и поля" (А.Ф. Иоффе – советский физик). Это фундаментальная база для теоретической подготовки инженера, без которой его успешная работа невозможна. Предложенное издание облегчает студенту слушание лекций и самостоятельную работу, при этом преследовалась цель изложения материала с достаточной полнотой и ясностью при весьма ограниченном объеме. Предполагается издание четырех частей лекций: механика, молекулярная физика и термодинамика; электричество и магнетизм; колебания, волны и оптика. Предлагаемая вниманию читателя первая часть посвящена механике – разделу физики, в котором изучается движение тел в пространстве и времени. Динамические законы и законы сохранения импульса, момента импульса и энергии представляют собой основные законы механики, они же составляют основное содержание лекций по механике.

Предлагаемые лекции по курсу общей физики должны помочь студентам технических специальностей ВлГУ в изучении курса. Максимальное внимание уделено раскрытию физического смысла основных законов и понятий физики. Стиль изложения соответствует этой цели: логичность, доступность и разумная строгость выкладок и доказательств, учитывающих уровень знаний студентов первого курса. Наиболее важные определения и понятия подчёркнуты, а главные формулы заключены в рамки, что облегчает студентам работу при изучении материала. Лекции сопровождаются примерами и вопросами для самоконтроля. Совершенно необходимо параллельно с изучением теоретического материала решать задачи, например, из пособия [7]. Краткость, ограниченный объём лекций позволяет студентам в условиях дефицита времени, например при подготовке к экзаменам, успеть усвоить основные законы и понятия физики. Лекции также могут быть полезны и преподавателям.

ВНИМАНИЕ! ПОСОБИЕ ОБЛЕГЧАЕТ РАБОТУ СТУДЕНТУ, НО НЕ ЗАМЕНЯЕТ САМИ ЛЕКЦИИ!

Лекция № 1

Вопросы для самоконтроля

1. Дайте определения скалярного и векторного произведения векторов.

2. Что такое радиус-вектор?

3. Какое движение называется поступательным?

4. В чём заключается принцип Галилея? Что устанавливают преобразования Галилея?

5. Что такое скорость? Как найти модуль скорости?

6. Какова ориентация векторов тангенциального и нормального ускорений? Запишите соответствующие выражения для них.

Лекция № 2

Центробежная сила инерции

Пусть на некотором диске имеется радиальная направляющая, на которую наденем шарик, привязанный к оси диска пружиной (рис. 2.3). При раскручивании диска шарик растягивает пружину до тех пор, пока упругая сила не станет равной .

Рис. 2.3

где центростремительное ускорение;

угловая скорость.

Относительно системы (диск) шарик покоится. Это можно формально объяснить тем, что в системе кроме силы на шарик действует сила инерции , направленная вдоль радиуса от оси вращения диска:

где единичный вектор, направленный к центру диска.

Эта сила называется центробежной силой инерции. Она возникает во вращающихся (неинерциальных) системах отсчёта независимо от того, покоится тело в этой системе или движется относительно неё со скоростью .

Сила Кориолиса

Густав Кориолис (1792 – 1873) – французский учёный в области механики.

При движении тела ( ) в неинерциальной вращающейся системе отсчёта кроме центробежной силы возникает еще одна сила инерции, называемая силой Кориолиса.

Возьмём горизонтально расположенный диск, вращающийся относительно инерциальной системы отсчёта с постоянной угловой скоростью (её определение будет в лекции № 3) (рис. 2.4). Допустим, что по окружности радиусом R равномерно движется привязанная нитью к оси диска материальная точка (частица) со скоростью относительно диска. Её скорость относительно Земли имеет модуль .

Центростремительное ускорение:

Сила натяжения нити:

где ускорение частицы относительно диска. Перенося в левую часть, а в правую, получим:

или

(Формально это выглядит как 2-й закон Ньютона).

Здесь центробежная сила инерции;

сила Кориолиса, которую можно представить в виде векторного произведения:

Многие течения в мировом океане, а также ветры-пассаты обязаны своим происхождением силе Кориолиса. Силы Кориолиса необходимо учитывать при движении ракет и т.д.

5. Центр инерции. Определение.Центром инерции (центром масс) системы материальных точек (частиц) называется точка С, положение которой задаётся радиус-вектором , определённым следующим образом:

где масса й частицы; радиус-вектор, определяющий положение этой частицы; масса системы.

Замечание: в однородном поле сил тяжести центр инерции совпадает с центром тяжести системы.

Вопросы для самоконтроля

1. Сформулируйте 1-й закон Ньютона. Что он устанавливает?

2. Сформулируйте 2-й закон Ньютона. Приведите пример использования этого закона как уравнения движения.

3. Сформулируйте 3-й закон Ньютона. Всегда ли он справедлив?

4. Когда возникает необходимость рассматривать силы инерции? Являются ли эти силы реальными?

5. Когда возникает центробежная сила инерции? Как ее рассчитывают?

6. При каких условиях возникает сила Кориолиса? Чему она равна?

7. Дайте определение центра инерции (центра масс).

8. Сформулируйте и докажите теорему о движении центра инерции (масс).

Лекция № 3

Свободные оси

Определение. Ось вращения тела, положение которой в пространстве остаётся неизменным без действия на неё внешних сил, называется свободной.

Можно доказать, что в любом теле существует три взаимно перпендикулярных оси, проходящие через центр масс тела, которые могут служить свободными осями. Они называются главными осями инерции тела. Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней. Вращение вокруг главных осей с наибольшим и наименьшим (экстремальными) моментами инерции оказывается устойчивым, а вращение вокруг оси со средним моментом – неустойчивым. Этот факт является достаточно важным при проектировании конструкций с вращающимися частями.

4. Момент силы. Пусть О – какая-либо точка, относительно которой рассматривается момент вектора силы. Обозначим радиус-вектор, проведённый из этой точки к точке приложения силы (Рис. 3.8).

Рис. 3.8

Определение. Моментом силы относительно точки О называется векторное произведение радиуса-вектора на силу :

Раскрывая векторное произведение, получим где плечо силы (длина перпендикуляра, опущенного из точки О на линию действия силы).

В соответствии с определением векторного произведения вектор направлен перпендикулярно плоскости, в которой лежат векторы и в соответствии с правилом правого винта (буравчика).

Определение. Момент силы относительно оси , проходящей через точку О, есть проекция на эту ось вектора момента силы относительно точки, лежащей на этой же оси.

как проекция на ось является скалярной величиной.

Момент импульса

Пусть материальная точка массой движется со скоростью относительно точки О, а радиус-вектор этой материальной точки, проведённый из точки О (рис. 3.9).

Определение. Моментом импульса материальной точки относительно точки О называется векторное произведение радиуса-вектора на вектор импульса :

Направление перпендикулярно плоскости, в которой лежат векторы и , в соответствии с правилом правого винта, например момент импульса электрона, двигающегося по круговой орбите в боровской модели атома.

Свяжем момент импульса с моментом инерции и угловой скоростью. Пусть радиус-вектор некоторой частицы массой лежит в плоскости рис. 3.10, скорость перпендикулярна ей («от нас»), частица движется по окружности радиусом .

Модуль момента импульса . Линейную скорость можно связать с угловой относительно оси как , тогда . Проекция вектора на ось вращения равна

. Как видно из рис. 3.10, , т.е.

Для системы материальных точек (твёрдого тела) выражение связи , и формально такое, как и для материальной точки:

Но под здесь подразумевается сумма моментов инерции материальных точек системы:

Можно показать (см., например, в [1]), что для однородного тела, симметричного относительно оси вращения, суммарный момент импульса тела . Он направлен вдоль оси вращения в ту же сторону, что и , т.е.

(Для несимметричного тела в общем случае не совпадает по направлению с вектором ).

5. Уравнение моментов. В дальнейших преобразованиях условимся для упрощения записи индекс 0 у , и других величин не писать, но подразумевать, что он есть.

Продифференцируем выражение для момента импульса материальной точки: . .

Учтём, что , а .

Рассмотрим первое слагаемое (см. в лекции № 1 «Векторное произведение»).

= (так как угол между и равен нулю).

Второе слагаемое в выражении для

(по определению момента силы).

В результате получаем:

Уравнение моментов (оно связывает момент импульса с моментом силы).

Производная по времени момента импульса материальной точки относительно точки О равна моменту действующей силы относительно точки О.

Вопросы для самоконтроля

1. Какое движение называется вращательным?

2. Как определяют угловую скорость и угловое ускорение?

3. Что является мерой инертности при вращательном движении?

4. Дайте определение момента инерции материальной точки и момента инерции твёрдого тела.

5. Как вычисляют моменты инерции для сплошного цилиндра и тонкого стержня?

6. Сформулируйте теорему Штейнера.

7. Что называется свободной осью? Какие оси называют главными осями инерции?

8. Дайте определения момента силы и момента импульса материальной точки относительно некоторой точки.

9. Как связан момент импульса с моментом инерции и угловой скоростью?

10. Выведите уравнение моментов.

11. Запишите уравнение динамики вращательного движения относительно оси .

12. Что называется гироскопом?

13. Что такое прецессия? От чего зависит скорость прецессии?

14. Что называется гироскопическим эффектом?

Лекция № 4

ЗАКОНЫ СОХРАНЕНИЯ

План

1. Закон сохранения импульса. Однородность пространства.

2. Закон сохранения момента импульса. Изотропия пространства.

3. Работа, мощность. Энергия кинетическая и потенциальная. Понятие силового поля. Консервативные силы.

4. Связь между потенциальной энергией и силой.

5. Закон сохранения механической энергии. Однородность времени.

6. Значение законов сохранения в механике.

1. Закон сохранения импульса. Рассмотрим произвольную систему взаимодействующих частиц. Введём понятие импульса системы как

где импульс i-й частицы.

Продифференцируем по времени:

По 2-му закону Ньютона , где сила, действующая на i-ю частицу со стороны других частиц системы (внутренние силы); сила, действующая на эту же частицу со стороны других тел, не входящих в рассматриваемую систему (внешние силы). Подставим в , получим

Сумма всех внутренних сил по 3-му закону Ньютона (силы взаимодействия между частицами системы попарно одинаковы по модулю и противоположны по направлению).

, т.е. производная импульса системы по времени равна векторной сумме внешних сил, действующих на систему.

Система материальных точек называетсяизолированой, если отсутствуют внешние силы (либо их действие скомпенсировано).

Если , то .

Закон сохранения импульса

Импульс изолированной системы не изменяется при любых процессах, протекающих внутри системы.

Закон сохранения импульса связан с однородностью пространства: параллельный перенос замкнутой системы с одного места пространства в другое, поставив при этом все тела в те же условия (без изменения расположения и скоростей), в каких они находились в прежнем положении, не отразится на ходе всех последующих явлений.

Необходимо отметить, что на Земле нет идеальных изолированных систем, так как на любую пару взаимодействующих тел действуют внешние силы (например силы тяжести на пару взаимодействующих тел пушка-снаряд) и закон сохранения импульса выполняется в проекции на горизонтальную ось, так как проекция сил тяжести на эту ось равна нулю. Другой случай, когда внутренние силы много больше внешних (например при взрыве гранаты), и последними можно пренебречь.

Подумайте, как с помощью закона сохранения импульса объяснить принцип реактивного движения.

2. Закон сохранения момента импульса. Пусть имеется произвольная система частиц. Введём момент импульса данной системы (момент импульса – величина аддитивная), где момент импульса i-й частицы. Продифференцируем это выражение:

Для i-й частицы из уравнения моментов:

где момент внутренних сил;

момент внешних сил.

Подставляя , получаем:

где и суммарные моменты соответственно внутренних и внешних сил.

По 3-му закону Ньютона внутренние силы попарно одинаковы по модулю, противоположны по направлению и лежат на данной прямой, т.е. имеют одинаковое плечо. Поэтому моменты сил каждой пары внутренних сил равны по модулю и противоположны по направлению, т.е. уравновешивают друг друга, и, значит, суммарный момент всех внутренних сил равен нулю, т.е. , соответственно:

Для изолированной системы

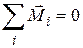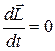Закон сохранения момента импульса: момент импульса замкнутой системы частиц остаётся постоянным.

Если система движется в поле силы тяжести Земли, то легко показать, что относительно любой вертикальной оси момент силы тяжести равен нулю и закон сохранения момента импульса выполняется в проекции на вертикальную ось, т.е. ( вертикальная ось), и соответственно:

(Например, фигурист на льду, резко прижав руки к туловищу, увеличивает свою угловую скорость вращения).

Закон сохранения момента импульса связан с изотропностью пространства: поворот замкнутой системы в пространстве на любой угол не отражается на ходе всех последующих явлений.

3. Работа, мощность. Энергия кинетическая и потенциальная. Пусть частица под действием силы совершает перемещение по некоторой траектории 1 – 2. В общем случае сила в процессе движения может меняться как по модулю, так и по направлению. Рассмотрим элементарное перемещение , в пределах которого силу можно считать постоянной (рис. 4.1).

Элементарной работой силы на перемещении называется скалярное произведение:

, где элементарный путь,

а проекция вектора на вектор .

Интегрируя по всем элементарным участкам пути от точки 1 до точки 2, получим работу силы при перемещении частицы от точки 1 до точки 2.

Работа, совершаемая в единицу времени, называется мощностью.

Полученное скалярное произведение силы на скорость точки приложения силы называется мгновенной мощностью.

(Работа на конечном перемещении, отнесённая к соответствующему времени перемещения, называется средней мощностью на данном участке:

Свяжем работу с кинетической энергией. Как было показано:

По 2-му закону Ньютона в проекции на направление движения . Из связи пути со скоростью , тогда

или

Таким образом, работа, совершаемая силой при движении, равна изменению (приращению) величины , которая называется кинетической энергией:

Интегрируя, получим:

(в дифференциальной форме ), т.е. изменение кинетической энергии на некотором перемещении равно алгебраической сумме работ всех сил, действующих на частицу на том же перемещении.

Кинетическую энергию иногда называют энергией движения.

Прежде чем перейти к понятию потенциальной энергии, дадим определения:

1. Силовым полем называется область пространства, в каждой точке которого на помещённую туда частицу действует сила.

2. Стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от формы пути, а зависит только от положения этих точек, называют потенциальным, а сами силы – консервативными.

Примем какую-либо точку пространства за начало отсчёта и будем рассматривать работу, совершаемую при переносе частицы из произвольной точки в точку О (рис. 4.2). Так как работа сил потенциального поля не зависит от формы пути, то остаётся зависимость её только от положения точки относительно точки О, т.е. будет некоторой функцией радиуса-вектора точки . Обозначим эту функцию .

Функцию называют потенциальной энергией частицы в данном поле. Различают собственную потенциальную энергию системы, зависящую при данном характере взаимодействия только от относительного расположения частиц системы, т.е. от её конфигурации, а также внешнюю потенциальную энергию, характеризующую взаимодействие данной системы с другими телами.

Найдём работу сил потенциального поля при перемещении частиц из точки 1 в точку 2. Так как эта работа не зависит от пути, выберем путь, проходящий через точку О (рис. 4.3).

Согласно равенству

Работа сил поля на пути 1 – 2 равна убыли потенциальной энергии частицы в данном поле. Для элементарного перемещения

4. Связь между потенциальной энергией и силой. Работа сил поля на элементарном перемещении:

С другой стороны, , отсюда , , т.е. проекция силы поля – вектора в данной точке на направление перемещения равна с обратным знаком производной потенциальной энергии по данному направлению. Например, для направления вдоль оси Х: .

При перемещении в произвольном направлении в проекции на оси координат ; ; ; т.е. проекции вектора на оси координат равны взятым с обратным знаком частным производным потенциальной энергии по Вектор , как и любой вектор, можно представить через его компоненты: . Подставим вместо соответствующие производные потенциальной энергии, получим:

Выражение в скобках есть градиент потенциальной энергии:

По определению градиент скалярной функции есть вектор, направленный в сторону быстрейшего возрастания этой функции и численно равный производной по направлению.

В результате получим:

(или , градиент обозначен – «набла»), т.е. сила поля равна со знаком минус градиенту потенциальной энергии частицы в данной точке поля (Иллюстрация этого положения на рис. 4.4 для произвольной точки А в потенциальном поле).

5. Закон сохранения механической энергии. Рассмотрим замкнутую систему тел, в которой действующие силы консервативны. Для любых сил , а для консервативных сил . Из этих двух равенств следует, что

полная механическая энергия системы.

Закон сохранения механической энергии: полная механическая энергия замкнутой системы частиц, на которую действуют только консервативные силы, остаётся постоянной в процессе движения системы.

В основе закона сохранения энергии лежит однородность времени, которая означает, что если в два любых момента времени все тела замкнутой системы поставить в совершенно одинаковые условия, то, начиная с этих моментов, все явления в ней будут протекать совершенно одинаково.

6. Значение законов сохранения в механике. Важная роль законов сохранения обусловлена рядом причин:

1. Законы сохранения не зависят ни от траектории частиц, ни от характера действующих сил. Поэтому они позволяют получить ряд весьма общих и существенных заключений о свойствах различных механических процессов, не вникая в их детальное рассмотрение, с помощью уравнений движения. Если, например, выясняется, что какой-то процесс противоречит законам сохранения, то сразу можно утверждать: этот процесс невозможен, и бессмысленно пытаться его осуществить.

2. Тот факт, что законы сохранения не зависят от характера действия сил, позволяет использовать их даже тогда, когда силы вообще не известны. В этих случаях законы сохранения являются единственным и незаменимым инструментом исследования.

3. Привлечение законов сохранения очень часто позволяет получить решение наиболее простым и изящным путём, избавляет от громоздких и утомительных расчётов.

Вопросы для самоконтроля

1. В чём состоит закон сохранения импульса? Следствием каких законов является закон сохранения импульса?

2. Сформулируйте и выведите закон сохранения момента импульса.

3. Что называется механической работой? Напишите формулу для расчёта работы постоянной и переменной силы.

4. При каком значении угла между направлением силы и перемещением работа равна нулю? Имеет наибольшее значение?

5. Что называется мгновенной мощностью? Средней мощностью?

6. Как связаны изменение кинетической энергии и работа сил, действующих на материальную точку?

7. Какое поле называется потенциальным? Какие силы называются консервативными?

8. Что называется потенциальной энергией?

9. Как связана потенциальная энергия частицы с силой поля, действующего на частицу, в данной точке? Дайте определение градиента скалярной функции координат. Как направлен градиент?

10. Сформулируйте закон сохранения механической энергии для замкнутой системы.

Лекция № 5

Уравнение Бернулли

Рассмотрим стационарное течение идеальной несжимаемой жидкости. Выделим трубку тока, а в ней объём жидкости, ограниченной стенками узкой трубки тока и перпендикулярными к линии тока сечениями и . За некоторое время этот объём сместится вдоль трубки тока, причём граница объёма получит перемещение , а граница перемещение (рис. 5.5).

Работа, совершаемая при этом силами давления, равна приращению полной механической энергии: , заключённой в рассматриваемом объёме жидкости (на рис. 5.5 между сечениями 1 и 2).

где вследствие несжимаемости жидкости; , а (на рисунке эти объёмы заштрихованы).

Полная энергия рассматриваемого объёма жидкости слагается из кинетической энергии и потенциальной энергии в поле сил земного тяготения. Возьмём сечения S трубки тока и перемещения настолько малыми, чтобы всем точкам каждого из заштрихованных объёмов можно было приписать одни и те же значения скорости , давления и высоты h. Приращение полной энергии (это разность полных энергий заштрихованных объёмов):

так как , то

Приравняв А и DЕ, сократив на и перенеся члены с одинаковыми индексами в одну сторону, получим:

Заметим, что уравнение вполне строго лишь при , т.е. для одной и той же линии тока. Так как и были выбраны произвольно, то можно утверждать, что для любой линии тока в стационарно текущей идеальной и несжимаемой жидкости выполняется условие (уравнение Бернулли):

Уравнение выражает для движущейся жидкости закон сохранения механической энергии.

Для горизонтальной линии тока:

Если скорость течения вдоль линии тока возрастает, то давление падает, и наоборот. Уравнение используется, например, в аэродинамических измерениях скорости потока газа. Обычно измеряют полное давление и статическое давление P в исследуемой точке потока, а значение скорости определяют как .

4. Течение вязкой жидкости. Формула Пуазейля. Для практических применений представляет особый интерес течение в круглой трубе (нефте- и газопроводы). Измерения показывают, что при медленном течении скорость частиц жидкости изменяется от нуля в непосредственной близости к стенкам трубы до максимума на оси трубы.

Найдём закон изменения

12 3 4 5 6 7 Следующая ⇒