Относительно неподвижной оси

В проекции на ось предыдущее уравнение запишется:

а так как , то , если , то . Так как проекция углового ускорения на ось , то получим уравнение динамики вращательного движения относительно оси Z и сравним с уравнением динамики для поступательного движения (2-й закон Ньютона).

Соответствие очевидно:

Поступательное движение			Вращательное движение

Замечание: если вокруг оси вращается однородное симметричное тело, то , и тогда очевидно:

(Угловое ускорение совпадает по направлению с вектором момента силы).

6. Гироскопы (от греч. круг, смотрю, наблюдаю).

Гироскопом называется массивное симметричное тело, вращающееся с большой угловой скоростью вокруг своей оси симметрии.

Рассмотрим поведение гироскопа на примере волчка (рис. 3.11). Опыт показывает, что если ось вращающегося волчка наклонена к вертикали, то волчок не падает, а совершает так называемое прецессионное движение (прецессию) – т.е. его ось описывает конус вокруг вертикали с некоторой угловой скоростью , причём чем больше скорость вращения волчка, тем меньше угловая скорость прецессии ( ).

Из уравнения моментов следует:

Приращение совпадает по направлению с моментом внешних сил, относительно точки О. Момент силы тяжести , как видно из рис. 3.11, перпендикулярен моменту импульса, т.е. , следовательно, приращение момента импульса . В результате вектор (и ось волчка) будут поворачиваться вместе с вектором вокруг вертикали, описывая круговой конус с углом полураствора .

Найдём связь между , и :

или в векторном виде , сравнивая с , получаем уравнение для угловой скорости прецессии.

Из уравнения видно, что момент силы определяет угловую скорость прецессии, а не ускорение. Это означает, что мгновенное устранение момента приводит к мгновенному исчезновению и прецессии, т.е. прецессия не обладает инерцией.

Гироскопический эффект

Рассмотрим эффект, возникающий при вынужденном вращении оси гироскопа. Пусть ось гироскопа укреплена в -образной подставке, которую мы будем поворачивать вокруг оси (рис. 3.12).

Рис. 3.12

Если момент импульса гироскопа направлен вправо, то при таком повороте за время вектор получит приращение вектор, направленный перпендикулярно . Согласно уравнению это означает, что на гироскоп действует момент силы , совпадающий по направлению с вектором . Момент обусловлен возникновением пары сил , действующих на ось гироскопа со стороны подставки. Ось гироскопа, в свою очередь, в соответствии с 3-им законом Ньютона будет действовать на подставку с силами . Эти силы называются гироскопическими. Они создают гироскопический момент . Появление гироскопических сил называют гироскопическим эффектом.

Замечание: в узком смысле гироскопическим эффектом иногда называют движение волчка не в сторону действия силы, а перпендикулярно к ней.

Примеры возникновения гироскопического эффекта: гироскопическое давление на подшипники у роторов турбин, компрессоров на кораблях, самолётах при поворотах, виражах.

Гироскопы являются основными узлами в гирокомпасах, в которых используется свойство гироскопов с тремя степенями свободы: его ось стремится устойчиво сохранить в мировом пространстве приданное ей первоначальное направление. Если ось направить на какую-либо звезду, то при любых перемещениях прибора и случайных толчках она будет указывать на эту звезду.

Вопросы для самоконтроля

1. Какое движение называется вращательным?

2. Как определяют угловую скорость и угловое ускорение?

3. Что является мерой инертности при вращательном движении?

4. Дайте определение момента инерции материальной точки и момента инерции твёрдого тела.

5. Как вычисляют моменты инерции для сплошного цилиндра и тонкого стержня?

6. Сформулируйте теорему Штейнера.

7. Что называется свободной осью? Какие оси называют главными осями инерции?

8. Дайте определения момента силы и момента импульса материальной точки относительно некоторой точки.

9. Как связан момент импульса с моментом инерции и угловой скоростью?

10. Выведите уравнение моментов.

11. Запишите уравнение динамики вращательного движения относительно оси .

12. Что называется гироскопом?

13. Что такое прецессия? От чего зависит скорость прецессии?

14. Что называется гироскопическим эффектом?

Лекция № 4

ЗАКОНЫ СОХРАНЕНИЯ

План

1. Закон сохранения импульса. Однородность пространства.

2. Закон сохранения момента импульса. Изотропия пространства.

3. Работа, мощность. Энергия кинетическая и потенциальная. Понятие силового поля. Консервативные силы.

4. Связь между потенциальной энергией и силой.

5. Закон сохранения механической энергии. Однородность времени.

6. Значение законов сохранения в механике.

1. Закон сохранения импульса. Рассмотрим произвольную систему взаимодействующих частиц. Введём понятие импульса системы как

где импульс i-й частицы.

Продифференцируем по времени:

По 2-му закону Ньютона , где сила, действующая на i-ю частицу со стороны других частиц системы (внутренние силы); сила, действующая на эту же частицу со стороны других тел, не входящих в рассматриваемую систему (внешние силы). Подставим в , получим

Сумма всех внутренних сил по 3-му закону Ньютона (силы взаимодействия между частицами системы попарно одинаковы по модулю и противоположны по направлению).

, т.е. производная импульса системы по времени равна векторной сумме внешних сил, действующих на систему.

Система материальных точек называетсяизолированой, если отсутствуют внешние силы (либо их действие скомпенсировано).

Если , то .

Закон сохранения импульса

Импульс изолированной системы не изменяется при любых процессах, протекающих внутри системы.

Закон сохранения импульса связан с однородностью пространства: параллельный перенос замкнутой системы с одного места пространства в другое, поставив при этом все тела в те же условия (без изменения расположения и скоростей), в каких они находились в прежнем положении, не отразится на ходе всех последующих явлений.

Необходимо отметить, что на Земле нет идеальных изолированных систем, так как на любую пару взаимодействующих тел действуют внешние силы (например силы тяжести на пару взаимодействующих тел пушка-снаряд) и закон сохранения импульса выполняется в проекции на горизонтальную ось, так как проекция сил тяжести на эту ось равна нулю. Другой случай, когда внутренние силы много больше внешних (например при взрыве гранаты), и последними можно пренебречь.

Подумайте, как с помощью закона сохранения импульса объяснить принцип реактивного движения.

2. Закон сохранения момента импульса. Пусть имеется произвольная система частиц. Введём момент импульса данной системы (момент импульса – величина аддитивная), где момент импульса i-й частицы. Продифференцируем это выражение:

Для i-й частицы из уравнения моментов:

где момент внутренних сил;

момент внешних сил.

Подставляя , получаем:

где и суммарные моменты соответственно внутренних и внешних сил.

По 3-му закону Ньютона внутренние силы попарно одинаковы по модулю, противоположны по направлению и лежат на данной прямой, т.е. имеют одинаковое плечо. Поэтому моменты сил каждой пары внутренних сил равны по модулю и противоположны по направлению, т.е. уравновешивают друг друга, и, значит, суммарный момент всех внутренних сил равен нулю, т.е. , соответственно:

Для изолированной системы

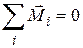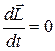Закон сохранения момента импульса: момент импульса замкнутой системы частиц остаётся постоянным.

Если система движется в поле силы тяжести Земли, то легко показать, что относительно любой вертикальной оси момент силы тяжести равен нулю и закон сохранения момента импульса выполняется в проекции на вертикальную ось, т.е. ( вертикальная ось), и соответственно:

(Например, фигурист на льду, резко прижав руки к туловищу, увеличивает свою угловую скорость вращения).

Закон сохранения момента импульса связан с изотропностью пространства: поворот замкнутой системы в пространстве на любой угол не отражается на ходе всех последующих явлений.

3. Работа, мощность. Энергия кинетическая и потенциальная. Пусть частица под действием силы совершает перемещение по некоторой траектории 1 – 2. В общем случае сила в процессе движения может меняться как по модулю, так и по направлению. Рассмотрим элементарное перемещение , в пределах которого силу можно считать постоянной (рис. 4.1).

Элементарной работой силы на перемещении называется скалярное произведение:

, где элементарный путь,

а проекция вектора на вектор .

Интегрируя по всем элементарным участкам пути от точки 1 до точки 2, получим работу силы при перемещении частицы от точки 1 до точки 2.

Работа, совершаемая в единицу времени, называется мощностью.

Полученное скалярное произведение силы на скорость точки приложения силы называется мгновенной мощностью.

(Работа на конечном перемещении, отнесённая к соответствующему времени перемещения, называется средней мощностью на данном участке:

Свяжем работу с кинетической энергией. Как было показано:

По 2-му закону Ньютона в проекции на направление движения . Из связи пути со скоростью , тогда

или

Таким образом, работа, совершаемая силой при движении, равна изменению (приращению) величины , которая называется кинетической энергией:

Интегрируя, получим:

(в дифференциальной форме ), т.е. изменение кинетической энергии на некотором перемещении равно алгебраической сумме работ всех сил, действующих на частицу на том же перемещении.

Кинетическую энергию иногда называют энергией движения.

Прежде чем перейти к понятию потенциальной энергии, дадим определения:

1. Силовым полем называется область пространства, в каждой точке которого на помещённую туда частицу действует сила.

2. Стационарное силовое поле, в котором работа силы поля на пути между двумя любыми точками не зависит от формы пути, а зависит только от положения этих точек, называют потенциальным, а сами силы – консервативными.

Примем какую-либо точку пространства за начало отсчёта и будем рассматривать работу, совершаемую при переносе частицы из произвольной точки в точку О (рис. 4.2). Так как работа сил потенциального поля не зависит от формы пути, то остаётся зависимость её только от положения точки относительно точки О, т.е. будет некоторой функцией радиуса-вектора точки . Обозначим эту функцию .

Функцию называют потенциальной энергией частицы в данном поле. Различают собственную потенциальную энергию системы, зависящую при данном характере взаимодействия только от относительного расположения частиц системы, т.е. от её конфигурации, а также внешнюю потенциальную энергию, характеризующую взаимодействие данной системы с другими телами.

Найдём работу сил потенциального поля при перемещении частиц из точки 1 в точку 2. Так как эта работа не зависит от пути, выберем путь, проходящий через точку О (рис. 4.3).

Согласно равенству

Работа сил поля на пути 1 – 2 равна убыли потенциальной энергии частицы в данном поле. Для элементарного перемещения

4. Связь между потенциальной энергией и силой. Работа сил поля на элементарном перемещении:

С другой стороны, , отсюда , , т.е. проекция силы поля – вектора в данной точке на направление перемещения равна с обратным знаком производной потенциальной энергии по данному направлению. Например, для направления вдоль оси Х: .

При перемещении в произвольном направлении в проекции на оси координат ; ; ; т.е. проекции вектора на оси координат равны взятым с обратным знаком частным производным потенциальной энергии по Вектор , как и любой вектор, можно представить через его компоненты: . Подставим вместо соответствующие производные потенциальной энергии, получим:

Выражение в скобках есть градиент потенциальной энергии:

По определению градиент скалярной функции есть вектор, направленный в сторону быстрейшего возрастания этой функции и численно равный производной по направлению.

В результате получим:

(или , градиент обозначен – «набла»), т.е. сила поля равна со знаком минус градиенту потенциальной энергии частицы в данной точке поля (Иллюстрация этого положения на рис. 4.4 для произвольной точки А в потенциальном поле).

5. Закон сохранения механической энергии. Рассмотрим замкнутую систему тел, в которой действующие силы консервативны. Для любых сил , а для консервативных сил . Из этих двух равенств следует, что

полная механическая энергия системы.

Закон сохранения механической энергии: полная механическая энергия замкнутой системы частиц, на которую действуют только консервативные силы, остаётся постоянной в процессе движения системы.

В основе закона сохранения энергии лежит однородность времени, которая означает, что если в два любых момента времени все тела замкнутой системы поставить в совершенно одинаковые условия, то, начиная с этих моментов, все явления в ней будут протекать совершенно одинаково.

6. Значение законов сохранения в механике. Важная роль законов сохранения обусловлена рядом причин:

1. Законы сохранения не зависят ни от траектории частиц, ни от характера действующих сил. Поэтому они позволяют получить ряд весьма общих и существенных заключений о свойствах различных механических процессов, не вникая в их детальное рассмотрение, с помощью уравнений движения. Если, например, выясняется, что какой-то процесс противоречит законам сохранения, то сразу можно утверждать: этот процесс невозможен, и бессмысленно пытаться его осуществить.

2. Тот факт, что законы сохранения не зависят от характера действия сил, позволяет использовать их даже тогда, когда силы вообще не известны. В этих случаях законы сохранения являются единственным и незаменимым инструментом исследования.

3. Привлечение законов сохранения очень часто позволяет получить решение наиболее простым и изящным путём, избавляет от громоздких и утомительных расчётов.

Вопросы для самоконтроля

1. В чём состоит закон сохранения импульса? Следствием каких законов является закон сохранения импульса?

2. Сформулируйте и выведите закон сохранения момента импульса.

3. Что называется механической работой? Напишите формулу для расчёта работы постоянной и переменной силы.

4. При каком значении угла между направлением силы и перемещением работа равна нулю? Имеет наибольшее значение?

5. Что называется мгновенной мощностью? Средней мощностью?

6. Как связаны изменение кинетической энергии и работа сил, действующих на материальную точку?

7. Какое поле называется потенциальным? Какие силы называются консервативными?

8. Что называется потенциальной энергией?

9. Как связана потенциальная энергия частицы с силой поля, действующего на частицу, в данной точке? Дайте определение градиента скалярной функции координат. Как направлен градиент?

10. Сформулируйте закон сохранения механической энергии для замкнутой системы.

Лекция № 5

⇐ Предыдущая 1 2 3 456 7 Следующая ⇒