ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ

План

1. Первый закон Ньютона и понятие инерциальной системы отсчёта.

2. Второй закон Ньютона как уравнение движения. Понятия массы, силы, импульса.

3. Третий закон Ньютона и пределы его применения.

4. Неинерциальные системы отсчёта. Абсолютные и относительные скорости и ускорения. Силы инерции (центробежная сила и сила Кориолиса).

5. Центр инерции (центр масс). Теорема о движении центра инерции.

1. 1-й закон Ньютона. Материальная точка, не подверженная внешним воздействиям, либо находится в покое, либо движется равномерно и прямолинейно. Такое тело называется свободным, его движение – свободным движением, или движением по инерции.

Классическая механика постулирует, что существует система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно. Такая система называется инерциальной системой отсчёта. Таким образом, 1-й закон Ньютона выражает критерий инерциальности системы отсчёта.

2. 2-й закон Ньютона. Производная импульса материальной точки по времени равна действующей на неё силе.

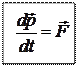
где – импульс (количество движения), векторная величина, равная для материальной точки произведению её массы на скорость и направленная вдоль ;

– масса – мера инертности тел.

Импульс механической системы равен геометрической сумме импульсов всех точек системы.

Сила в механике – мера механического действия на данное материальное тело других тел. Это действие может иметь место как при непосредственном контакте, так и через посредство создаваемых телами полей (электромагнитным, полем тяготения). Сила – величина векторная и в каждый момент времени характеризуется численным значением, направлением в пространстве и точкой приложения. Сложение сил производится по правилу параллелограмма. В современной физике различают 4 вида взаимодействий:

1) гравитационное (обусловлено всемирным тяготением);

2) электромагнитное (осуществляется через электрические и магнитные поля);

3) сильное, или ядерное (обеспечивающее связь частиц в атомном ядре);

4) слабое (ответственное за многие процессы распада элементарных частиц).

Пример использования 2-го закона Ньютона как уравнения движения:

Дано: , , .	Решение: , , , . При , , , , , . При , , , .
Найти:

3. 3-й закон Ньютона. Силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки.

Третий закон, как и 1-й и 2-й, справедливы лишь в инерциальных системах отсчёта. Кроме того, отступление от 3-го закона наблюдается в случае движения тел со скоростями, сравнимыми со скоростью света.

В случае движущихся зарядов необходимо учитывать также взаимодействие с магнитными полями, создаваемыми ими. Пусть два положительных заряда и двигаются со скоростями и (рис. 2.1). На каждый заряд со стороны другого действует как кулоновская , так и лоренцева силы . Направления векторов индукции магнитных полей и , создаваемых частицами и , определяются по правилу правого винта (буравчика).

Рис. 2.1

Магнитные силы Лоренца и не совпадают по направлению. Результирующие силы и не равны друг другу и не направлены противоположно.

4. Неинерциальные системы отсчёта. Силы инерции. Изобразим две системы отсчёта, из которых К является инерциальной, а система движется относительно К с некоторым ускорением и, следовательно, неинерциальная (рис. 2.2).

Рис. 2.2

В случае, когда система движется относительно К поступательно:

где радиус-вектор точки m в системе К; радиус-вектор начала координат ; радиус-вектор точки m в системе . Продифференцируем дважды выражение :

где ускорение частицы m в системе К ;

– ускорение начала системы относительно системы К;

– ускорение частицы в системе .

; умножим обе части этого уравнения на m, получим

, здесь по 2-му закону Ньютона сила, действующая на частицу со стороны других тел , тогда:

То есть относительно системы частица ведёт себя так, как если бы кроме силы на нее действует дополнительная сила . Эта сила называется силой инерции.

Движение относительно выбранной условно неподвижной системы называется абсолютным. Вектор даёт абсолютную скорость, абсолютное ускорение, а и относительные скорость и ускорение.

Центробежная сила инерции

Пусть на некотором диске имеется радиальная направляющая, на которую наденем шарик, привязанный к оси диска пружиной (рис. 2.3). При раскручивании диска шарик растягивает пружину до тех пор, пока упругая сила не станет равной .

Рис. 2.3

где центростремительное ускорение;

угловая скорость.

Относительно системы (диск) шарик покоится. Это можно формально объяснить тем, что в системе кроме силы на шарик действует сила инерции , направленная вдоль радиуса от оси вращения диска:

где единичный вектор, направленный к центру диска.

Эта сила называется центробежной силой инерции. Она возникает во вращающихся (неинерциальных) системах отсчёта независимо от того, покоится тело в этой системе или движется относительно неё со скоростью .

Сила Кориолиса

Густав Кориолис (1792 – 1873) – французский учёный в области механики.

При движении тела ( ) в неинерциальной вращающейся системе отсчёта кроме центробежной силы возникает еще одна сила инерции, называемая силой Кориолиса.

Возьмём горизонтально расположенный диск, вращающийся относительно инерциальной системы отсчёта с постоянной угловой скоростью (её определение будет в лекции № 3) (рис. 2.4). Допустим, что по окружности радиусом R равномерно движется привязанная нитью к оси диска материальная точка (частица) со скоростью относительно диска. Её скорость относительно Земли имеет модуль .

Центростремительное ускорение:

Сила натяжения нити:

где ускорение частицы относительно диска. Перенося в левую часть, а в правую, получим:

или

(Формально это выглядит как 2-й закон Ньютона).

Здесь центробежная сила инерции;

сила Кориолиса, которую можно представить в виде векторного произведения:

Многие течения в мировом океане, а также ветры-пассаты обязаны своим происхождением силе Кориолиса. Силы Кориолиса необходимо учитывать при движении ракет и т.д.

5. Центр инерции. Определение.Центром инерции (центром масс) системы материальных точек (частиц) называется точка С, положение которой задаётся радиус-вектором , определённым следующим образом:

где масса й частицы; радиус-вектор, определяющий положение этой частицы; масса системы.

Замечание: в однородном поле сил тяжести центр инерции совпадает с центром тяжести системы.

⇐ Предыдущая 1 234 5 6 7 Следующая ⇒