Непрерывные дроби и их связь с алгоритмом Евклида
30.Пусть  – любое вещественное число. Обозначим буквой q1наибольшее целое число, не превосходящее
– любое вещественное число. Обозначим буквой q1наибольшее целое число, не превосходящее  .
.
При нецелом  имеем
имеем  ;
;  . Точно так же при нецелых
. Точно так же при нецелых 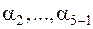 имеем
имеем
 ,
,
...............
 ;
; 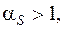
ввиду чего получаем следующее разложение  в непрерывную дробь:
в непрерывную дробь:
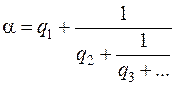
.
. (1)
.
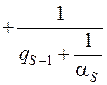
Если  – иррациональное, то и всякое
– иррациональное, то и всякое 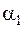 – иррациональное (при рациональном
– иррациональное (при рациональном  ввиду (1) рациональным оказалось бы и
ввиду (1) рациональным оказалось бы и  ) и указанный процесс может быть неограниченно продолжен.
) и указанный процесс может быть неограниченно продолжен.
Если же  – рациональное и, следовательно, может быть представлено рациональной несократимой дробью
– рациональное и, следовательно, может быть представлено рациональной несократимой дробью  с положительным знаменателем, то указанный процесс будет конечен и может быть выполнен с помощью алгоритма Евклида. Действительно, имеем:
с положительным знаменателем, то указанный процесс будет конечен и может быть выполнен с помощью алгоритма Евклида. Действительно, имеем:

 ,
,

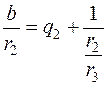
...........................

 ,
,
 ;
;  ,
,
 ;
;  ,
,
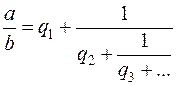
.
.
.

Числа  ..., участвующие в разложении числа
..., участвующие в разложении числа  в непрерывную дробь, называются неполными частными (в случае рационального
в непрерывную дробь, называются неполными частными (в случае рационального  это будут, согласно
это будут, согласно  , неполные частные последовательных делений алгоритма Евклида), дроби же
, неполные частные последовательных делений алгоритма Евклида), дроби же
 ,
,  ,
, 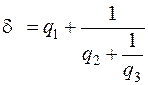 , ...
, ...
называются подходящими дробями.
Простой закон вычисления подходящих дробей получим, заметив, что  получается из
получается из 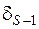 заменой в буквенном выражении для
заменой в буквенном выражении для 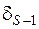 числа
числа  числом
числом  . Действительно, полагая ради единообразия Р0 = 1, Qo = 0, мы можем последовательно представить подходящие дроби в следующем виде (здесь равенство
. Действительно, полагая ради единообразия Р0 = 1, Qo = 0, мы можем последовательно представить подходящие дроби в следующем виде (здесь равенство  пишем, желая обозначить А символом РS, а В –символом QS):
пишем, желая обозначить А символом РS, а В –символом QS):
 ,
,
 ,
,
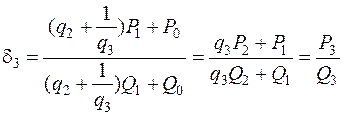
и т.д. и вообще при 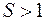
 (2)
(2)
Таким образом, числители и знаменатели подходящих дробей мы можем последовательно вычислять по формулам
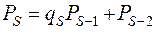
 (3)
(3)
Эти вычисления удобно делать по следующей схеме (два последних столбца пишем лишь в случае, когда 
 – несократимая дробь с положительным знаменателем:
– несократимая дробь с положительным знаменателем:  ):
):
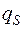
|
| 
| 
| …
|
|
|
| …
| 
| 
|

| 1
| 
| 
| ...
| 
| 
| 
| …
| 
| a
|

| 0
| 1
| 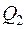
| …
| 
| 
| 
| ...
| 
| b
|
Пример. Разложим в непрерывную дробь несократимую дробь 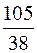 .
.
Здесь имеем
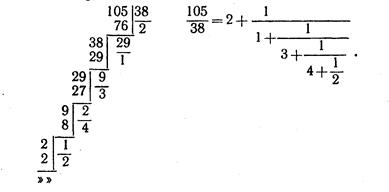
Поэтому указанная выше схема дает
При s > 0 имеем 
При S > 1 имеем 
Действительно, приняв обозначение hs = PsQs–1 – QsPs–1, мы при s = 1 получим h  = q
= q  . 0–1 . 1 = –1, a при s = 1 с помощью равенства (3) найдём hs = –hs–1. Отсюда получим hs–1 = (–1)s. Пользуясь же этим равенством при s > 1, легко найдём
. 0–1 . 1 = –1, a при s = 1 с помощью равенства (3) найдём hs = –hs–1. Отсюда получим hs–1 = (–1)s. Пользуясь же этим равенством при s > 1, легко найдём
 –
– 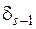 =
=  -
-  =
= 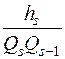 =
=  .
.
Пусть 1 < s, а если  – рациональная несократимая дробь
– рациональная несократимая дробь
 =
=  с положительным знаменателем, то пусть также s < n. Тогда
с положительным знаменателем, то пусть также s < n. Тогда  лежит между
лежит между 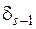 и
и  , причём ближе к
, причём ближе к  , нежели к
, нежели к 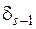 .
.
Действительно, заменив в равенстве (2) число q  числом
числом
q  +
+  , получим
, получим
 =
=  ,
,
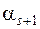 Q
Q  +
+  Q
Q  –
– 
 P
P  – P
– P  = 0,
= 0,
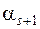 Q
Q  (
(  –
–  ) + Q
) + Q  (
(  –
–  ) = 0,
) = 0,
откуда убеждаемся, что первая из разностей, стоящих в скобках, и по знаку противоположна второй и численно (ввиду Q  > Q
> Q  ) меньше последней. А этим и доказываются наши утверждения.
) меньше последней. А этим и доказываются наши утверждения.
Мультипликативные функции
31.Функция  (а) называется мультипликативной, если она удовлетворяет двум следующим условиям:
(а) называется мультипликативной, если она удовлетворяет двум следующим условиям:
1. Эта функция определена для всех целых положительных а и не равна нулю, по меньшей мере при одном таком а.
2. Для любых положительных взаимно простых a1и а2имеем:
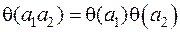
Пример. Нетрудно видеть, что мультипликативной является функция  , где s – любое вещественное или комплексное число.
, где s – любое вещественное или комплексное число.
32. Для всякой мультипликативной функции  (а) имеем
(а) имеем
 (1) = 1. Действительно, пусть
(1) = 1. Действительно, пусть  (а0) не равно нулю. Находим
(а0) не равно нулю. Находим
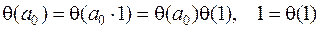
Свойство 31.2мультипликативной функции  (a) распространяется и на случай k > 2 попарно простых чисел а1, аг, а3, ..., ak.Действительно, имеем:
(a) распространяется и на случай k > 2 попарно простых чисел а1, аг, а3, ..., ak.Действительно, имеем:
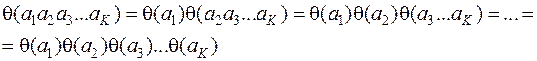
В частности, находим
 . (1)
. (1)
33. Обратно, мы всегда построим некоторую мультипликативную функцию  (a), если, положив
(a), если, положив  (1) = 1 и назначив произвольно значения для
(1) = 1 и назначив произвольно значения для  (Р
(Р 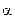 ), отвечающих положительным степеням простых чисел, в общем случае определим эту функцию равенством (1).
), отвечающих положительным степеням простых чисел, в общем случае определим эту функцию равенством (1).
Действительно, если  представлено в виде произведения
представлено в виде произведения  двух взаимно простых чисел а1и а2, то справедливо тождество
двух взаимно простых чисел а1и а2, то справедливо тождество
 ,
,
левая часть которого является произведением чисел  , отвечающих всем сомножителям вида
, отвечающих всем сомножителям вида  числа а, а правая часть является тем же произведением, но разбитым на два взаимно простых произведения, одно из которых
числа а, а правая часть является тем же произведением, но разбитым на два взаимно простых произведения, одно из которых  является произведением чисел
является произведением чисел  , отвечающих всем сомножителям вида
, отвечающих всем сомножителям вида  числа
числа 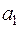 , другое же
, другое же  является произведением чисел
является произведением чисел  , отвечающих всем сомножителям видам
, отвечающих всем сомножителям видам  числа
числа  .
.
Пример.Мультипликативную функцию можно построить, взяв  (1) = 1 и
(1) = 1 и  (рa) = 2, если
(рa) = 2, если  > 0. Тогда при k > 0 будем иметь
> 0. Тогда при k > 0 будем иметь  . В частности, найдем:
. В частности, найдем:
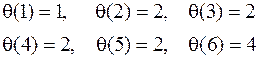
34.Произведение  (а) =
(а) =  1 (а)
1 (а)  2 (а) двух мультипликативных функций
2 (а) двух мультипликативных функций  1(а) и
1(а) и  2 (а) также является мультипликативной функцией.
2 (а) также является мультипликативной функцией.
Действительно, имеем 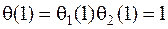
Кроме того, при 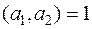 находим
находим
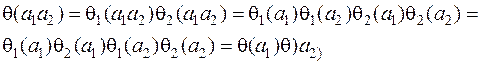
Доказанная теорема обобщается и на случай любого числа К > 2 мультипликативных функций
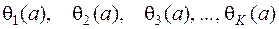
Действительно, пользуясь ею последовательно, убедимся в мультипликативности произведений:

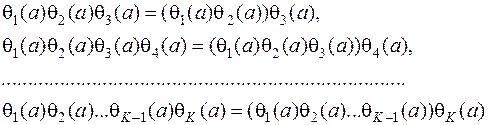
35.Пусть  – мультипликативная функция и а =
– мультипликативная функция и а =  – каноническое разложение числа а.. Тогда, обозначая символом
– каноническое разложение числа а.. Тогда, обозначая символом  сумму, распространенную на все делители d числа a, будем иметь
сумму, распространенную на все делители d числа a, будем иметь
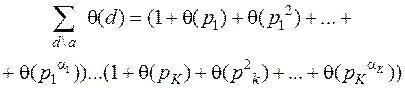
(В случае a = 1 правая часть считается равной 1.)
Чтобы доказать, что это тождество, раскроем скобки в его правой части. Тогда получим сумму всех (без пропусков и повторений) слагаемых вида
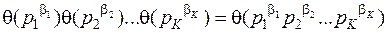
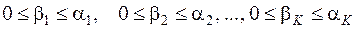
 А это (теорема 24) как раз и будет то, что стоит в левой части тождества.
А это (теорема 24) как раз и будет то, что стоит в левой части тождества.
Популярное:

