
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Последовательное соединение резистивного и емкостного элементов
где
Параллельное соединение резистивного и емкостного элементов
Для цепи на рис. 18 имеют место соотношения:
Векторная диаграмма токов для данной цепи, называемая треугольником токов, приведена на рис. 19. Ей соответствует уравнение в комплексной форме где Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 20. Для комплексного сопротивления цепи на рис. 18 можно записать Необходимо отметить, что полученный результат аналогичен известному из курса физики выражению для эквивалентного сопротивления двух параллельно соединенных резисторов. Параллельное соединение резистивного и индуктивного элементов
Для цепи на рис. 21 можно записать Векторной диаграмме токов (рис. 22) для данной цепи соответствует уравнение в комплексной форме где Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 23.
Литература 1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. 2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с. Контрольные вопросы и задачи 1. В чем сущность реактивных сопротивлений? 2. Какой из элементов: резистор, катушку индуктивности или конденсатор – можно использовать в качестве шунта для наблюдения за формой тока? 3. Почему катушки индуктивности и конденсаторы не используются в цепях постоянного тока? 4. В ветви на рис. 12 5. В ветви на рис. 15 6. В цепи на рис. 18 7. Протекающий через катушку индуктивности | |||||||||||||
| Лекция N 5. Закон Ома для участка цепи с источником ЭДС. |
Объединяя оба случая, получим
или для постоянного тока
Формулы (1) и (2) являются аналитическим выражением закона Ома для участка цепи с источником ЭДС, согласно которому ток на участке цепи с источником ЭДС равен алгебраической сумме напряжения на зажимах участка цепи и ЭДС, деленной на сопротивление участка. В случае переменного тока все указанные величины суть комплексы. При этом ЭДС и напряжение берут со знаком “+”, если их направление совпадает с выбранным направлением тока, и со знаком “-”, если их направление противоположно направлению тока.
Основы символического метода расчета цепей
Расчет цепей переменного синусоидального тока может производиться не только путем построения векторных диаграмм, но и аналитически – путем операций с комплексами, символически изображающими синусоидальные ЭДС, напряжения и токи. Достоинством векторных диаграмм является их наглядность, недостатком – малая точность графических построений. Применение символического метода позволяет производить расчеты цепей с большой степенью точности. Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной форме. Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин. 1. Первый закон Кирхгофа в комплексной форме:
2. Второй закон Кирхгофа в комплексной форме:
или применительно к схемам замещения с источниками ЭДС
3. Соответственно матричная запись законов Кирхгофа в комплексной форме имеет вид: § первый закон Кирхгофа:
§ второй закон Кирхгофа
Пример. Дано:
Решение:
1. 2. 3. 4. Принимая начальную фазу напряжения за нуль, запишем: Тогда 5. Поскольку ток распределяется обратно пропорционально сопротивлению ветвей (это вытекает из закона Ома), то 6. 7. Аналогичный результат можно получить, составив для данной схемы уравнения по законам Кирхгофа в комплексной форме
или после подстановки численных значений параметров схемы
Специальные методы расчета
Режим работы любой цепи полностью характеризуется уравнениями, составленными на основании законов Кирхгофа. При этом необходимо составить и решить систему с n неизвестными, что может оказаться весьма трудоемкой задачей при большом числе n ветвей схемы. Однако, число уравнений, подлежащих решению, может быть сокращено, если воспользоваться специальными методами расчета, к которым относятся методы контурных токов и узловых потенциалов.
Метод контурных токов Идея метода контурных токов: уравнения составляются только по второму закону Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи графа Направления истинных и контурных токов выбираются произвольно. Выбор положительных направлений перед началом расчета может не определять действительные направления токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его истинное направление противоположно.
Выразим токи ветвей через контурные токи: Обойдя контур aeda, по второму закону Кирхгофа имеем Поскольку то Таким образом, получили уравнение для первого контура относительно контурных токов. Аналогично можно составить уравнения для второго, третьего и четвертого контуров: совместно с первым решить их относительно контурных токов и затем по уравнениям, связывающим контурные токи и токи ветвей, найти последние. Однако данная система уравнений может быть составлена формальным путем: При составлении уравнений необходимо помнить следующее: члены на главной диагонали всегда пишутся со знаком “+”; знак “+” перед остальными членами ставится в случае, если через общее сопротивление если i-й и k- й контуры не имеют общих сопротивлений, то в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением контурного тока, и “-”, если не совпадает. В нашем случае, для первого уравнения системы, имеем: Следует обратить внимание на то, что, поскольку Если в цепи содержатся помимо источников ЭДС источники тока, то они учитываются в левых частях уравнений как известные контурные токи: k- й контурный ток, проходящий через ветвь с k- м источником тока равен этому току
Метод узловых потенциалов Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно Пусть имеем схему по рис. 4, в которой примем
Запишем уравнение по первому закону Кирхгофа для узла а: и подставим значения входящих в него токов, определенных выше: Сгруппировав соответствующие члены, получим: Аналогично можно записать для узла b: Как и по методу контурных токов, система уравнений по методу узловых потенциалов может быть составлена формальным путем. При этом необходимо руководствоваться следующими правилами: 1. В левой части i-гоуравнения записывается со знаком “+”потенциал Из сказанного следует, что все члены 2. В правой части i-гоуравнения записывается так называемый узловой ток В заключение отметим, что выбор того или иного из рассмотренных методов определяется тем, что следует найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений. При расчете токов при одинаковом числе уравнений предпочтительнее использовать метод контурных токов, так как он не требует дополнительных вычислений с использованием закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных цепей, но не удобен при расчете цепей со взаимной индуктивностью.
Литература
1. Основы теории цепей: Учеб.для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. 2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с . Контрольные вопросы и задачи
1. В ветви на рис. 1 Ответ: 2. В чем заключается сущность символического метода расчета цепей синусоидального тока? 3. В чем состоит сущность метода контурных токов? 4. В чем состоит сущность метода узловых потенциалов? 5. В цепи на рис. 5 Ответ: 6. В цепи на рис. 6 Ответ:
| |||||||||||||||||||||||||||||
| Лекция N 6. Основы матричных методов расчета электрических цепей. |
Рассмотренные методы расчета электрических цепей – непосредственно по законам Кирхгофа, методы контурных токов и узловых потенциалов – позволяют принципиально рассчитать любую схему. Однако их применение без использования введенных ранее топологических матриц рационально для относительно простых схем. Использование матричных методов расчета позволяет формализовать процесс составления уравнений электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно существенно при расчете сложных разветвленных схем.
 Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.
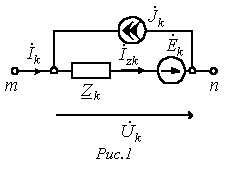
Пусть имеем схему по рис. 1, где Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.
Пусть имеем схему по рис. 1, где  - источник тока. В соответствии с рассмотренным нами ранее законом Ома для участка цепи с ЭДС для данной схемы можно записать: - источник тока. В соответствии с рассмотренным нами ранее законом Ома для участка цепи с ЭДС для данной схемы можно записать:
Однако, для дальнейших выкладок будет удобнеепредставить ток
Подставив (2) в (1), получим:
Формула (3) представляет собой аналитическое выражение закона Ома для участка цепи с источниками ЭДС и тока (обобщенной ветви). Соотношение (3) запишем для всех n ветвей схемы в виде матричного равенства или
где Z – диагональная квадратная (размерностью n x n) матрица сопротивлений ветвей, все элементы которой (взаимную индуктивность не учитываем), за исключением элементов главной диагонали, равны нулю. Соотношение (4) представляет собой матричную запись закона Ома. Если обе части равенства (4) умножить слева на контурную матрицу В и учесть второй закон Кирхгофа, согласно которому
то
то есть получили новую запись в матричной форме второго закона Кирхгофа.
Популярное:
|
Последнее изменение этой страницы: 2016-04-11; Просмотров: 1134; Нарушение авторского права страницы