
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Определение скоростей и ускорений
Планом скоростей (ускорений) механизма называется пучок векторов, выходящих из одной точки (полюса плана), каждый из которых в некотором масштабе изображает вектор абсолютной скорости (абсолютного ускорения) какой-либо точки механизма, а отрезки, соединяющие их концы, изображают векторы относительных скоростей (относительных ускорений).
Построение плана скоростей сводится к реализации известного положения теоретической механики, согласно которому при плоско-параллельном движении твёрдого тела (звена) скорость любой его точки равна векторной сумме скорости в поступательном переносном движении вместе с другой точкой, принятой в качестве полюса, и скорости её в относительном вращательном движении относительно этого полюса.
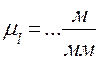 в исследуемом положении. Прежде необходимо определить параметры движения точки А. Её скорость по величине равна произведению угловой скорости в исследуемом положении. Прежде необходимо определить параметры движения точки А. Её скорость по величине равна произведению угловой скорости 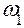 кривошипа 1 на его радиус кривошипа 1 на его радиус 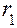 , т. е. , т. е. 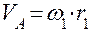 и направлена перпендикулярно кривошипу в сторону движения точки А. Ускорение точки А по величине равно произведению квадрата угловой скорости кривошипа также на его радиус, т. е. и направлена перпендикулярно кривошипу в сторону движения точки А. Ускорение точки А по величине равно произведению квадрата угловой скорости кривошипа также на его радиус, т. е. 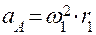 и направлено от точки А к точке О, так как совпадает с нормальной составляющей полного ускорения точки А из-за равенства нулю тангенциальной составляющей ускорения (угловое ускорение кривошипа принимается равным нулю). Точка А принадлежит не только кривошипу, но и шатуну 2 и принимается в качестве полюса относительного вращения точки В. Скорость точки В определяется векторным равенством и направлено от точки А к точке О, так как совпадает с нормальной составляющей полного ускорения точки А из-за равенства нулю тангенциальной составляющей ускорения (угловое ускорение кривошипа принимается равным нулю). Точка А принадлежит не только кривошипу, но и шатуну 2 и принимается в качестве полюса относительного вращения точки В. Скорость точки В определяется векторным равенством 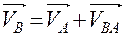 , т. е. скорость точки В равна скорости точки А плюс скорость точки В относительно точки А. В этом равенстве первое слагаемое правой части известно по величине и по направлению, второе слагаемое направлено перпендикулярно шатуну 2 в данном положении, т. е. известно по направлению, и, наконец, вектор левой части направлен параллельно направляющим ползуна. При этих условиях треугольник скоростей легко строится в предварительно выбранном масштабе , т. е. скорость точки В равна скорости точки А плюс скорость точки В относительно точки А. В этом равенстве первое слагаемое правой части известно по величине и по направлению, второе слагаемое направлено перпендикулярно шатуну 2 в данном положении, т. е. известно по направлению, и, наконец, вектор левой части направлен параллельно направляющим ползуна. При этих условиях треугольник скоростей легко строится в предварительно выбранном масштабе 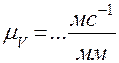 . . Построение плана ускорений производится в той же последовательности, что и план скоростей. При этом используется векторное равенство Используя планы, легко найти физические величины скоростей и ускорений, для этого необходимо измерить отрезки в миллиметрах, выражающие скорости и ускорения, и умножить их на соответствующий масштаб. Абсолютная скорость точки В: Относительная скорость точки В: Угловая скорость шатуна 2: Тангенциальное ускорения точки В относительно точки А:
Полное относительное ускорение: Угловое ускорение шатуна 2:
(метод графического дифференцирования) Основой метода служит известное положение математики, согласно которому производная функции, заданной в виде графика, в какой-либо её точке численно равна тангенсу угла наклона касательной, проведённой в этой точке к графику функции, то есть
Так как теория механизмов и машин имеет дело с именованными числами, то при определении величины тангенса необходимо учитывать масштабы по осям координат графика функции (рис. 4.4), тогда
Выберем горизонтальный отрезок произвольной длины и проведём из его левого конца наклонную прямую, параллельную касательной, а из правого конца – вертикальную прямую до пересечения с наклонной. Вычислим длину отрезка, полученного на вертикали и обозначенного на рис. 4.4 буквой
В правой части этого выражения переменной величиной является только
Таким образом мы убедились, что отрезок Для применения рассмотренной методики необходимо предварительно построить график или функции положения механизма, или график аналога скорости. Чтобы построить график производной, необходимо на продолжении оси абсцисс этого графика в левую сторону от оси ординат выбрать произвольный отрезок Вопросы для самопроверки 1. Сформулируйте задачи кинематического анализа механизмов с низшими парами. 2. Перечислите методы исследования кинематики механизмов. 3. Что должно быть задано для исследования кинематики механизма? 4. В чём заключается сущность аналитического метода исследования кинематики? 5. Что называется масштабом в ТММ? 6. Что такое разметка механизма? 7. Для чего строится разметка? 8. Как определяются скорость и ускорение конца кривошипа? 9. Запишите векторные уравнения для построения планов скоростей и ускорений и объясните их составляющие. Какое правило механики положено в основу этих уравнений? 10. Как определяются скорости и ускорения центра масс шатуна? 11. Как определить угловые скорость и ускорение стержневого звена? 12. Какое правило математики положено в основу графического дифференцирования функции, заданной в виде графика? 13. Приведите пример построении графика производной при заданном графике функции. 14. Как определяются масштабы по осям координат при построении графика производной?
Кинетостатика механизмов В этом разделе изучаются силы, действующие на звенья механизмов. Из-за ограниченности объёма данной работы здесь рассматриваются только механизмы с низшими кинематическими парами. Задачами этого раздела являются следующие. 1)Определение реакций в кинематических парах механизмов с целью их использования в дальнейшем для прочностных расчётов звеньев и элементов кинематических пар, сил трения, КПД и т. д. 2)Определение уравновешивающей силы или уравновешивающего момента на ведущем звене. Для решения этих задач необходимо знать 1)кинематическую схему механизма и кинематические размеры его звеньев. 2)массы и моменты инерции звеньев. 3)внешние силы, действующие в машинах (применительно к технологическим машинам должны быть известны силы полезного, т. е. технологического сопротивления, применительно к машинам-двигателям необходимо знать движущие силы). Расчёт сил инерции Расчёт сил инерции относится к предварительному расчёту, предшествующему основной задаче определения реакций в кинематических парах. Силы инерции возникают во всех случаях, когда звенья движутся непрямолинейно и/или неравномерно. Рассмотрим три вида движения звеньев. Популярное:
|
Последнее изменение этой страницы: 2016-05-03; Просмотров: 798; Нарушение авторского права страницы