Интерполяция функции с помощью первой формулы Ньютона

Определение значения функции в точке х = 1, 1 внутри интервала с помощью первой интерполяционной формулы Ньютона.

Составим таблицу конечных разностей таблично заданной функции (таблица 2.1).

Таблица 2.1 – Конечные разности таблично заданной функции (первая формула Ньютона)

τ _ХОЛ., с	S_ХОЛ., м
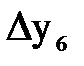
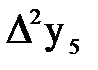
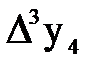
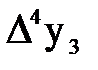
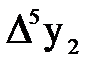
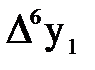
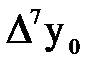
0, 20	0, 02	0, 01	0, 07	-0, 07	0, 07	-0, 12	0, 27	-0, 59
0, 40	0, 03	0, 08	0, 00	0, 00	-0, 05	0, 15	-0, 32
0, 60	0, 11	0, 08	0, 00	-0, 05	0, 1	-0, 17
0, 80	0, 19	0, 08	-0, 05	0, 05	-0, 07
1, 00	0, 27	0, 03	0, 00	-0, 02
1, 20	0, 30	0, 03	-0, 02
1, 40	0, 33	0, 01
1, 60	0, 34

За x₀ принимаем ближайшее к искомому значение х = 1, 1, т.е. x₀ = 1, 0 Так

как h = 0, 2, то .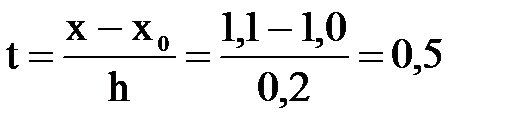

Далее записывается общий вид формулы Ньютона и её решение.

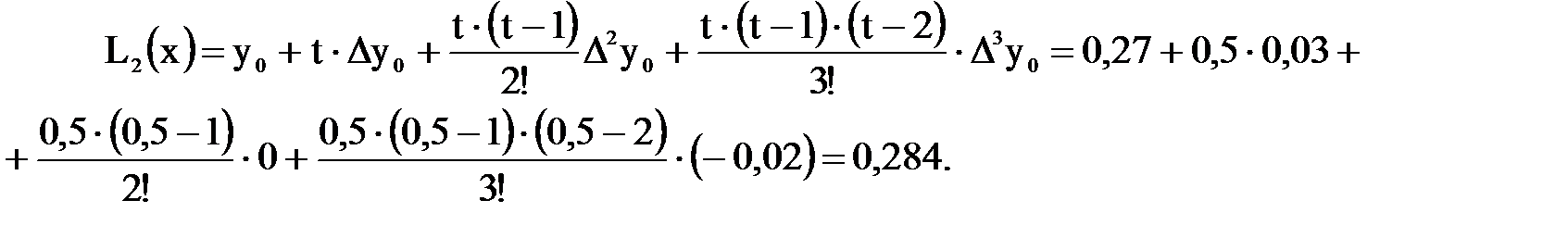
Интерполяция функции с помощью второй формулы Ньютона

Определение значения функции в точке х = 1, 1 внутри интервала с помощью второй интерполяционной формулы Ньютона.

Далее составляется таблица конечных разностей таблично заданной функции (смотри таблицу 2.1).

Примем x_n = 1, 6, тогда: .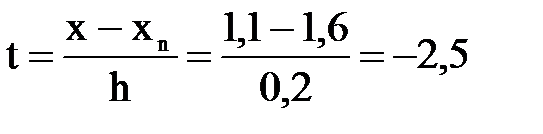

Далее записывается общий вид формулы Ньютона и её решение.

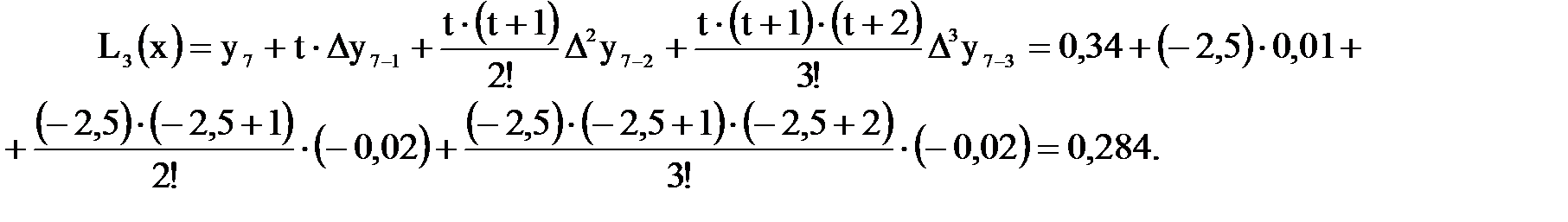
Экстраполяция функции с помощью первой формулы Ньютона

Определение значение функции в точке за пределами заданного интервала (аппроксимация назад) вблизи начального значения интервала x₀, т.е. х < x₀.

Далее составляется таблица конечных разностей таблично заданной функции (смотри таблицу 2.1).

За x₀ принимаем ближайшее к искомому значение х = 0, 19, 0, т.е. x₀ = 0, 2. Так как h = 0, 2, то .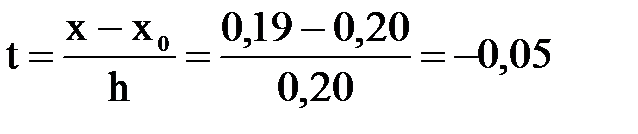

Далее записывается общий вид формулы Ньютона и её решение.

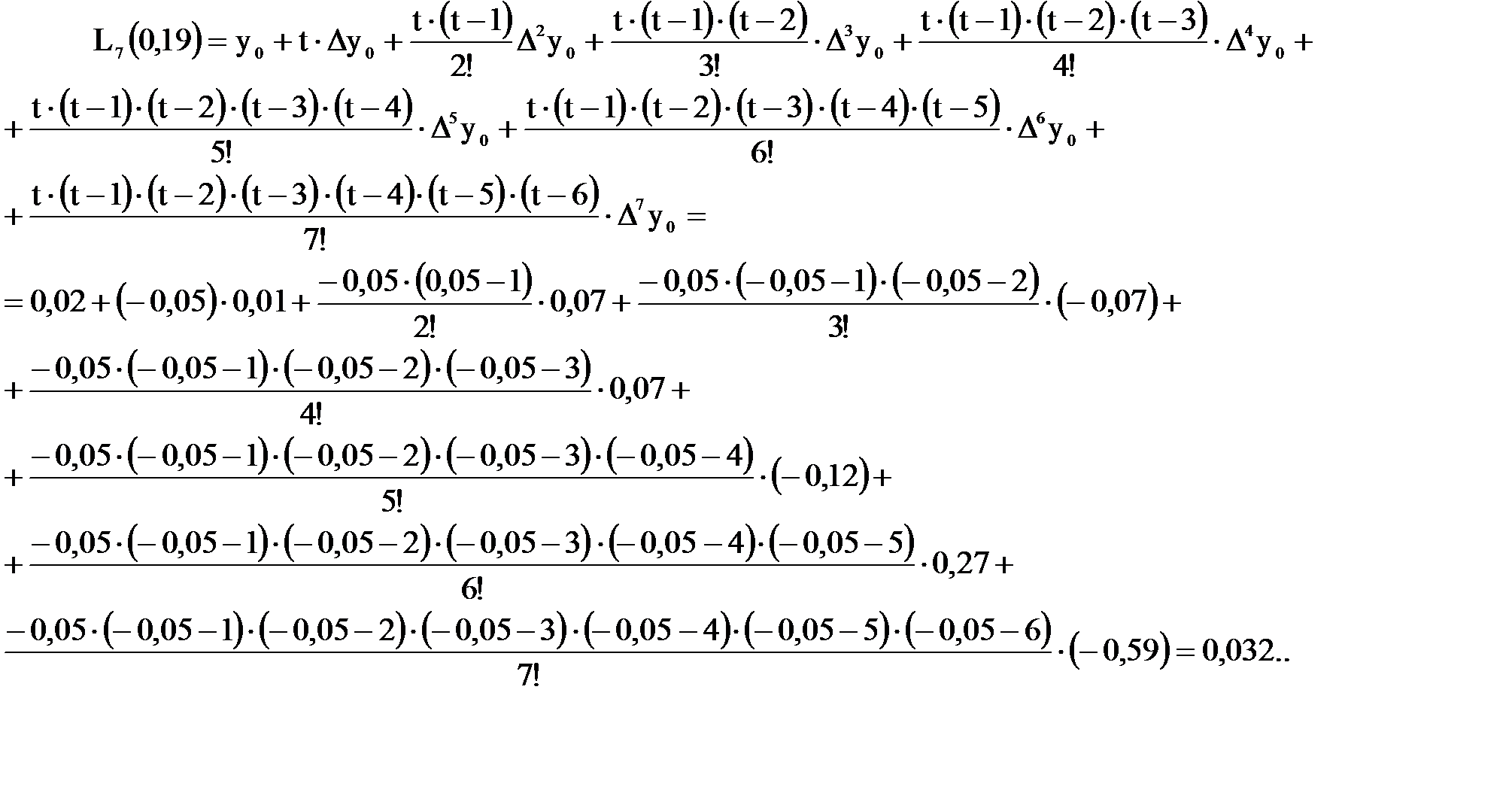
Экстраполяция функции с помощью второй формулы Ньютона

Определение значение функции в точке за пределами заданного интервала вблизи конечного значения интервала x_n, т.е. х > x_n.

Далее составляется таблица конечных разностей таблично заданной функции (смотри таблицу 2.1).

Примем x_n = 4, 0, тогда: .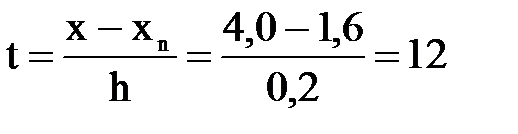

Далее записывается общий вид формулы Ньютона и её решение.

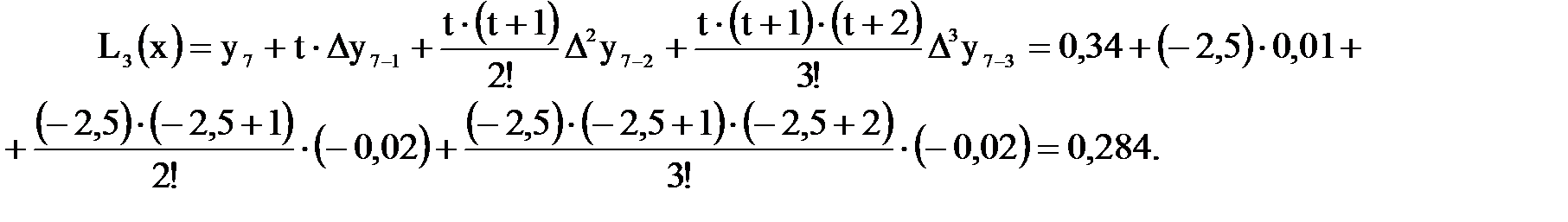
2.2.6 Аппроксимация функции методом неопределённых
коэффициентов

Аппроксимация функции полиномом 2-й степени по трём точкам (x₀, x₁, x₄) методом неопределённых коэффициентов.

Система алгебраических уравнений с тремя неизвестными а₀, а₁, а₂ примет вид:

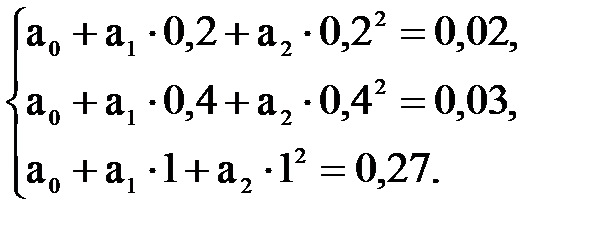
В матричной форме данная система будет выглядеть так:

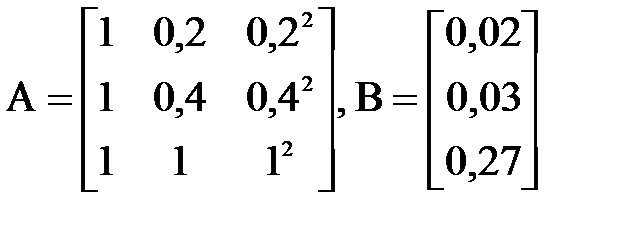Определитель матрицы А находится следующим образом:

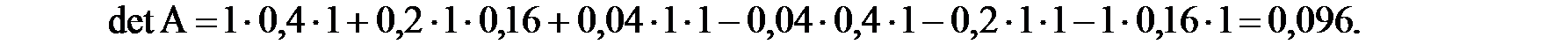
Если detА ≠ 0, то для матрицы А существует обратнаяматрица.

Присоединённая матрица А^* к матрице А находится следующим образом:

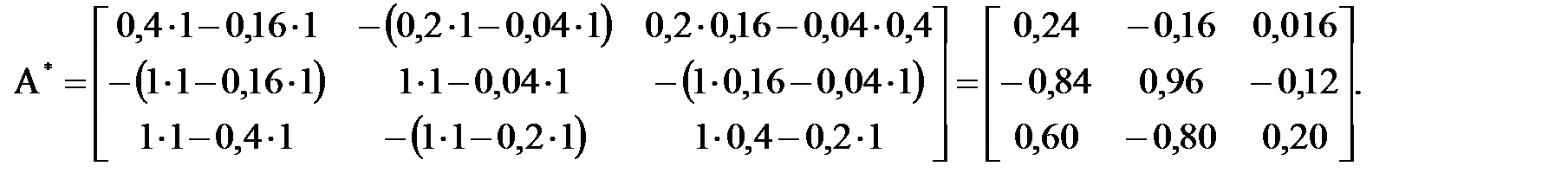
Необходимо заметить, что в присоединённой матрице элементы, сумма коэффициентов которых равна нечётному числу, меняют свой знак на противоположный (с₂₁, с₁₂, с₃₂, с₂₃).

Далее находится обратная матрица А^-1:

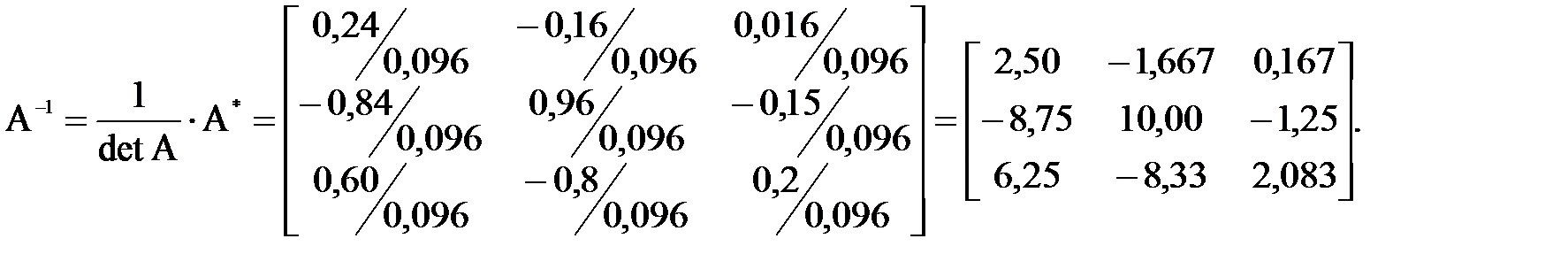
Далее по формуле (2.51) находятся искомые значения функции.

Аппроксимация функции методом наименьших квадратов

Аппроксимация функции полиномом 1-й степени по шести точкам методом наименьших квадратов.

Список литературы

1. Леушин, И.О. Лабораторный практикум по методам математического моделирования: Учебное пособие/ И.О. Леушин. — Н.Новгород: Изд-во «НГТУ», 2007. — 122 с.

2. Леушин, И.О. Моделирование процессов и объектов в металлургии: учебник для студентов вузов/ И.О. Леушин. — Н.Новгород: Изд-во «НГТУ им. Р.Е. Алексеева», 2010. — 181 с.

3. Леушин, И.О. Математическая обработка результатов экспериментов: методические указания к выполнению расчётно-графической работы/ И.О. Леушин, В.А. Решетов. — Н.Новгород: Изд-во «НГТУ», 2001. — 35 с.

Приложение А

(обязательное)

Листинг программы, реализованной в среде MathCAD

Лабораторная работа №2 Приёмы вторичной математической обработки данных Вариант № Группа: ФИО студента: Задание: 1) провести интерполяцию функции, заданной выборками Ах и Ву, различными способами и определить значения функции в двух точках внутри интервала; 2) провести экстраполяцию заданной функции с применением функции предсказания в пяти точках правее интервала; 3) оценить степень парной корреляции данных выборок Ах и Ву; 4) провести аппроксимацию заданной функции различными способами; 5) провести фильтрацию данных выборок Ах и Ву. Исходные данные:

Расположение точек заданной функции в поле хОу

Линейная интерполяция заданной функции

Значения функции в двух точках внутри интервала

Интерполяция заданной функции линейными сплайнами

Значения функции в двух точках внутри интервала

Интерполяция заданной функции квадратичными сплайнами

Значения функции в двух точках внутри интервала

Интерполяция заданной функции кубическими сплайнами

Значения функции в двух точках внутри интервала

Эксраполяция заданной функции функцией предсказания

< = Количество значений выборки Ву, по которым проводится экстраполяция

< = Количество точек для экстраполяции за пределами интервала

< = Длина выборки Ву

< = Значения функции в пяти точках справа от интервала

Оценка степени парной корреляции данных выборок Ах и Ву

Такое значение коэффициента парной корреляции свидетельствует о том, что связь между элементами выборок Ах и Ву близка к функциональной. Аппроксимация заданной функции полиномом 2-й степени прямым применением метода наименьших квадратов

Аппроксимация заданной функции полиномом 4-й степени прямым применением метода наименьших квадратов

Линейная регрессия данных выборок Ах и Ву

Линейная регрессия методом наименьших квадратов

Вычисление коэффициентов полинома

Линейная регрессия медтан-медианным методом

Вычисление коэффициентов полинома

Полиномиальная регрессия данных выборок Ах и Ву

Полиномиальная регрессия естественным аппроксимирующим полиномом 4-й степени

Полиномиальная регрессия участками квадратичных полиномов

Регрессия единственной аппроксимирующей логарифмической функцией

Аппроксимация заданной функции методом линейной регрессии общего вида Задание линейной комбинации функции

Аппроксимация заданной функции методом нелинейной регрессии общего вида Задание вида функции Первый элемент содержит приближающую функцию, остальные - её частные производные по параметрам