Тема7 Законы постоянного тока

⇐ ПредыдущаяСтр 3 из 3

1. Электропроводка должна выполняться из достаточно толстого провода, чтобы он сильно не нагревался и не создавал угрозы пожара. Если проводка рассчитана на максимальную силу тока 16 А и на погонном метре провода должно выделяться не более 2 Вт тепла, то диаметр медного провода (с учетом того, что удельное сопротивление меди равно 17 нОм·м) равен ______ мм.

Решение:
Мощность тока . Тогда мощность, выделяющаяся на погонном метре провода, . Отсюда диаметр провода

2. Вольтамперные характеристики активных элементов 1 и 2 цепи представлены на рисунке:

При напряжении 20 В отношение мощностей Р₁/Р₂ равно …

Решение:
Мощность, выделяемая на активных элементах, равна 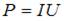, где 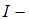сила тока, напряжение. Для напряжения 20 В из графика можно найти силу тока. Тогда .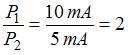

3. Напряжение на концах медного провода диаметром d и длиной l равно . Если взять медный провод диаметром d, но длиной 2l и увеличить напряжение в 4 раза, то среднее время дрейфа электронов от одного конца проводника до другого …

Решение:
Время, которое требуется в среднем для того, чтобы электроны продрейфовали на расстояние l, определяется соотношением , где – средняя скорость упорядоченного движения (дрейфа) электронов. Формула, связывающая силу тока со средней скоростью упорядоченного движения носителей тока, имеет вид , где q₀ – заряд носителей, в данном случае – электронов, n – их концентрация, S – площадь поперечного сечения проводника. С учетом закона Ома для участка цепи и формулы для сопротивления проводника 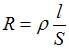получаем выражение для средней скорости направленного движения электронов , из которого следует, что не зависит от диаметра провода. Тогда время дрейфа . Таким образом, если взять медный провод диаметром d, но длиной 2l и увеличить напряжение в 4 раза, то среднее время дрейфа электронов от одного конца проводника до другого не изменится.

4. На рисунке показана зависимость силы тока в электрической цепи от времени:

Отношение заряда, прошедшего через поперечное сечение проводника за двадцать секунд, к заряду, прошедшему за последние пять секунд, равно …

Решение:
По определению сила тока в цепи 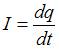. Отсюда 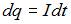, где – заряд, прошедший через поперечное сечение проводника за бесконечно малый промежуток времени . Заряд, прошедший за определенный промежуток времени, можно определить по формуле . Используя геометрический смысл определенного интеграла, найдем и Следовательно,

Тема 8 Магнитостатика

1. 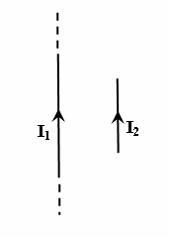Поле создано прямолинейным длинным проводником с током I₁. Если отрезок проводника с током I₂ расположен в одной плоскости с длинным проводником так, как показано на рисунке, то сила Ампера …

Решение:
На проводник с током в магнитном поле действует сила Ампера. В данном случае магнитное поле создается прямолинейным длинным проводником с током I₁. В соответствии с правилом правого винта (буравчика) вектор магнитной индукции в месте расположения отрезка проводника с током I₂ направлен перпендикулярно плоскости чертежа «от нас». В случае прямолинейного отрезка проводника с током в перпендикулярном проводнику магнитном поле для нахождения направления силы Ампера удобно воспользоваться правилом левой руки, согласно которому сила Ампера лежит в плоскости чертежа и направлена влево.

2. 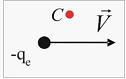На рисунке изображен вектор скорости движущегося электрона. Вектор магнитной индукции 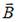поля, создаваемого электроном при движении, в точке С направлен …

Решение:
Индукция магнитного поля свободно движущегося заряда равна 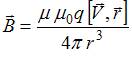, где 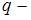заряд частицы, 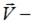скорость частицы, 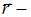радиус-вектор точки С. Используя определение векторного произведения, находим, что вектор 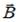направлен «на нас», но, учитывая отрицательный знак заряда частицы, получим окончательный ответ – вектор 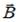направлен «от нас».

3. Протон влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции и начинает двигаться по окружности. При увеличении кинетической энергии протона (если 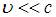) в 4 раза радиус окружности …

Решение:
Радиус окружности, по которой движется заряженная частица в магнитном поле 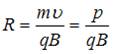, где p – импульс частицы, связанный с ее кинетической энергией (при условии, что 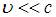) соотношением 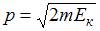. Тогда 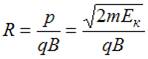, и при увеличении кинетической энергии протона в 4 раза радиус окружности увеличится в два раза.

4. 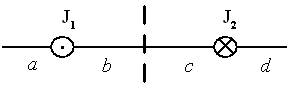На рисунке изображены сечения двух прямолинейных длинных параллельных проводников с противоположно направленными токами, причем 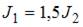. Индукция 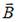магнитного поля равна нулю на участке …

Решение:
Линии магнитной индукции прямолинейных длинных проводников с токам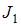и и 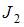представляют собой концентрические окружности, плоскости которых перпендикулярны проводникам, а центры лежат на их осях. Направления этих линий определяют правилом правого винта: направление вращения винта дает направление силовой линии магнитной индукции, если поступательное движение винта совпадает с направлением тока в проводнике. Индукция 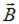результирующего магнитного поля определяется по принципу суперпозиции 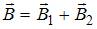и равна нулю, если векторы 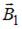и 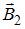противоположно направлены и равны по модулю. Это может быть только в точках интервалов а и d. Поскольку магнитная индукция прямолинейного длинного проводника с током вычисляется по формуле 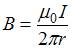, то модули векторов 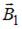и 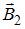равны, если 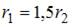, так как по условию 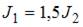. Следовательно, индукция 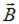результирующего магнитного поля равна нулю в некоторой точке интервала d.

⇐ Предыдущая 1 23