Тема1 Кинематика поступательного и вращательного движения

Тема1 Кинематика поступательного и вращательного движения

 

1. Твердое тело вращается вокруг неподвижной оси. Скорость точки, находящейся на расстоянии 10 см от оси, изменяется со временем в соответствии с графиком, представленным на рисунке.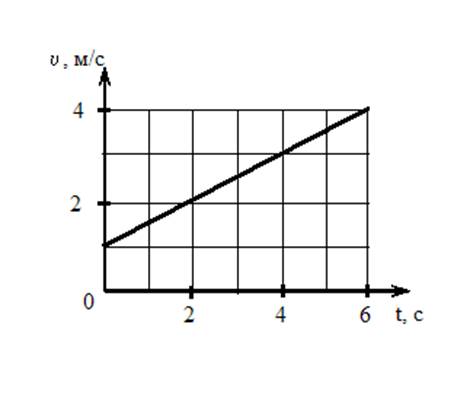
Угловое ускорение тела (в единицах СИ) равно…

Решение:

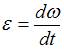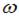По определению угловое ускорение тела, вращающегося вокруг неподвижной оси, , где – угловая скорость тела. Связь между модулями угловой скорости вращения тела и линейной скоростью точки, отстоящей от оси вращения на расстояние R, имеет вид 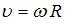. Отсюда 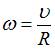, причем R = 10 см = 0, 1 м. Из представленного графика начальная скорость 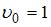м/с, ускорение 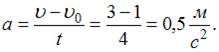Итак, зависимость скорости точки от времени в единицах СИ задается уравнением 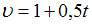, а зависимость угловой скорости вращения тела – уравнением 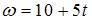. Тогда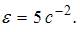

 

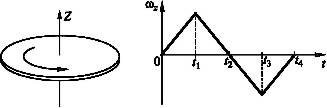
2. Диск вращается вокруг своей оси, изменяя проекцию угловой скорости 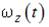так, как показано на рисунке. Вектор угловой скорости 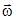и вектор углового ускорения 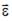направлены в одну сторону в интервалы времени …

Решение:

По определению угловое ускорение тела 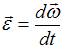, где 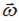– его угловая скорость. При вращении вокруг неподвижной оси векторы 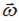и 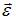коллинеарны, причем направлены в одну и ту же сторону, если вращение ускоренное, и в противоположные стороны, если вращение замедленное. Направление вектора 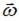связано с направлением вращения тела правилом правого винта. В интервале времени от 0 до 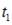вектор угловой скорости направлен вдоль оси OZ и, поскольку скорость увеличивается, вектор углового ускорения направлен так же. 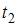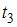В интервале времени от до вектор угловой скорости направлен против оси OZ, но скорость при этом также увеличивается, следовательно, вектор углового ускорения сонаправлен с вектором угловой скорости.

 

 

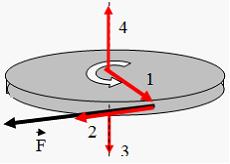
3. Диск равномерно вращается вокруг вертикальной оси в направлении, указанном на рисунке белой стрелкой. В некоторый момент времени к ободу диска была приложена сила, направленная по касательной.

Решение:

До остановки диска правильно изображает направление угловой скорости вектор …

Направление вектора угловой скорости 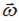связано с направлением вращения тела правилом правого винта. В данном случае вектор ориентирован в направлении 4. После приложения силы движение становится замедленным.

 

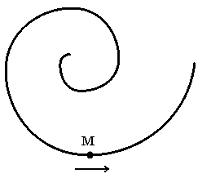
4. Точка М движется по спирали с равномерно убывающей скоростью в направлении, указанном стрелкой. При этом величина полного ускорения точки …

Решение:
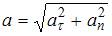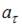Величина полного ускорения определяется соотношением , где и 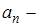тангенциальное и нормальное ускорения соответственно, причем 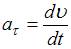, , 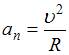где R – радиус кривизны траектории. Так как по условию скорость убывает равномерно, величина тангенциального ускорения остается постоянной. В то же время величина нормального ускорения уменьшается, поскольку при этом радиус кривизны траектории увеличивается, что видно из рисунка. Таким образом, полное ускорение точки уменьшается.

 

Тема 4 Работа. Энергия

1. Потенциальная энергия частицы задается функцией 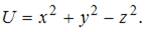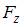-компонента (в Н) вектора силы, действующей на частицу в точке А (1, 2, 3), равна …
(Функция 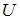и координаты точки А и заданы в единицах СИ.)

Решение:
Связь между потенциальной энергией частицы и соответствующей ей потенциальной силой имеет вид: 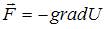, или 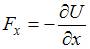, , 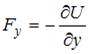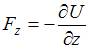. Таким образом,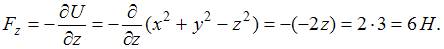

2. 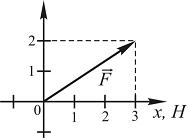На рисунке показан вектор силы, действующей на частицу:
Работа, совершенная этой силой при перемещении частицы из начала координат в точку с координатами (5; 2), равна ______ .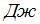

Решение:
По определению 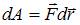. С учетом того, что 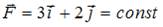(см. рис.),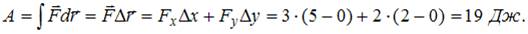

3. Частица совершила перемещение по некоторой траектории из точки M (3, 2) в точку N (2, –3). При этом на нее действовала сила 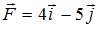(координаты точек и сила 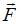заданы в единицах СИ). Работа, совершенная силой 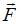, равна …

Решение:
По определению 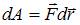. С учетом того, что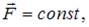

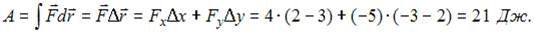
Тема5 Законы сохранения в механике

Тема 8 Магнитостатика

1. 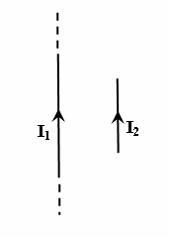Поле создано прямолинейным длинным проводником с током I₁. Если отрезок проводника с током I₂ расположен в одной плоскости с длинным проводником так, как показано на рисунке, то сила Ампера …

Решение:
На проводник с током в магнитном поле действует сила Ампера. В данном случае магнитное поле создается прямолинейным длинным проводником с током I₁. В соответствии с правилом правого винта (буравчика) вектор магнитной индукции в месте расположения отрезка проводника с током I₂ направлен перпендикулярно плоскости чертежа «от нас». В случае прямолинейного отрезка проводника с током в перпендикулярном проводнику магнитном поле для нахождения направления силы Ампера удобно воспользоваться правилом левой руки, согласно которому сила Ампера лежит в плоскости чертежа и направлена влево.

2. 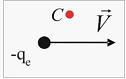На рисунке изображен вектор скорости движущегося электрона. Вектор магнитной индукции 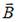поля, создаваемого электроном при движении, в точке С направлен …

Решение:
Индукция магнитного поля свободно движущегося заряда равна 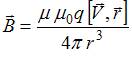, где 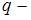заряд частицы, 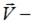скорость частицы, 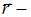радиус-вектор точки С. Используя определение векторного произведения, находим, что вектор 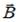направлен «на нас», но, учитывая отрицательный знак заряда частицы, получим окончательный ответ – вектор 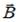направлен «от нас».

3. Протон влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции и начинает двигаться по окружности. При увеличении кинетической энергии протона (если 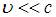) в 4 раза радиус окружности …

Решение:
Радиус окружности, по которой движется заряженная частица в магнитном поле 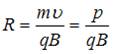, где p – импульс частицы, связанный с ее кинетической энергией (при условии, что 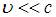) соотношением 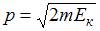. Тогда 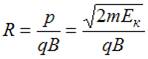, и при увеличении кинетической энергии протона в 4 раза радиус окружности увеличится в два раза.

4. 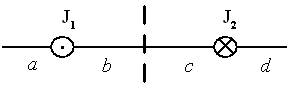На рисунке изображены сечения двух прямолинейных длинных параллельных проводников с противоположно направленными токами, причем 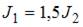. Индукция 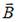магнитного поля равна нулю на участке …

Решение:
Линии магнитной индукции прямолинейных длинных проводников с токам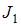и и 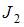представляют собой концентрические окружности, плоскости которых перпендикулярны проводникам, а центры лежат на их осях. Направления этих линий определяют правилом правого винта: направление вращения винта дает направление силовой линии магнитной индукции, если поступательное движение винта совпадает с направлением тока в проводнике. Индукция 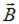результирующего магнитного поля определяется по принципу суперпозиции 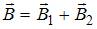и равна нулю, если векторы 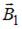и 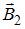противоположно направлены и равны по модулю. Это может быть только в точках интервалов а и d. Поскольку магнитная индукция прямолинейного длинного проводника с током вычисляется по формуле 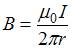, то модули векторов 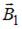и 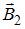равны, если 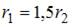, так как по условию 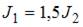. Следовательно, индукция 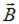результирующего магнитного поля равна нулю в некоторой точке интервала d.

Тема1 Кинематика поступательного и вращательного движения

 

1. Твердое тело вращается вокруг неподвижной оси. Скорость точки, находящейся на расстоянии 10 см от оси, изменяется со временем в соответствии с графиком, представленным на рисунке.
Угловое ускорение тела (в единицах СИ) равно…

Решение:

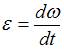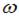По определению угловое ускорение тела, вращающегося вокруг неподвижной оси, , где – угловая скорость тела. Связь между модулями угловой скорости вращения тела и линейной скоростью точки, отстоящей от оси вращения на расстояние R, имеет вид 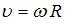. Отсюда 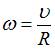, причем R = 10 см = 0, 1 м. Из представленного графика начальная скорость 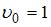м/с, ускорение 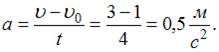Итак, зависимость скорости точки от времени в единицах СИ задается уравнением 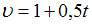, а зависимость угловой скорости вращения тела – уравнением 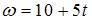. Тогда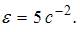

 

2. Диск вращается вокруг своей оси, изменяя проекцию угловой скорости 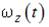так, как показано на рисунке. Вектор угловой скорости 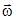и вектор углового ускорения 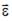направлены в одну сторону в интервалы времени …

Решение:

По определению угловое ускорение тела 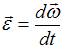, где 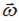– его угловая скорость. При вращении вокруг неподвижной оси векторы 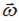и 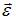коллинеарны, причем направлены в одну и ту же сторону, если вращение ускоренное, и в противоположные стороны, если вращение замедленное. Направление вектора 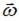связано с направлением вращения тела правилом правого винта. В интервале времени от 0 до 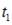вектор угловой скорости направлен вдоль оси OZ и, поскольку скорость увеличивается, вектор углового ускорения направлен так же. 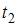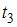В интервале времени от до вектор угловой скорости направлен против оси OZ, но скорость при этом также увеличивается, следовательно, вектор углового ускорения сонаправлен с вектором угловой скорости.

 

 

3. Диск равномерно вращается вокруг вертикальной оси в направлении, указанном на рисунке белой стрелкой. В некоторый момент времени к ободу диска была приложена сила, направленная по касательной.

Решение:

До остановки диска правильно изображает направление угловой скорости вектор …

Направление вектора угловой скорости 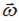связано с направлением вращения тела правилом правого винта. В данном случае вектор 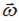ориентирован в направлении 4. После приложения силы движение становится замедленным.

 

4. Точка М движется по спирали с равномерно убывающей скоростью в направлении, указанном стрелкой. При этом величина полного ускорения точки …

Решение:
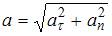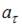Величина полного ускорения определяется соотношением , где и 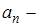тангенциальное и нормальное ускорения соответственно, причем 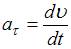, , 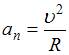где R – радиус кривизны траектории. Так как по условию скорость убывает равномерно, величина тангенциального ускорения остается постоянной. В то же время величина нормального ускорения уменьшается, поскольку при этом радиус кривизны траектории увеличивается, что видно из рисунка. Таким образом, полное ускорение точки уменьшается.

 

123Следующая ⇒

Поделиться:

Популярное:

1. A. обеспечение выполнения расписания движения, корректировка движения в случае необходимости, оказание техпомощи ПС на линии, принятие мер в случае ДТП и др.
2. Анализ движения рабочей силы
3. Безопасность движения поезда и риски потерь
4. Виды административных правонарушений в области дорожного движения.
5. Возможность физического движения
6. Возрождение олимпийского движения и его функционирование в настоящее время
7. Вопрос №29 Причины подъема общественного движения.
8. ВРАЖДЕБНОСТЬ СО СТОРОНЫ БЕЛОГО ДВИЖЕНИЯ
9. Глава 14. Проблемы международного спортивного движения
10. Глава 4. ПРЕОБРАЗОВАТЕЛИ ДВИЖЕНИЯ
11. Глава 76. Контроль передвижения босса.
12. Государственный экзамен по специальности 5В090100 – Организация перевозок, движения и эксплуатация транспорта