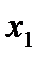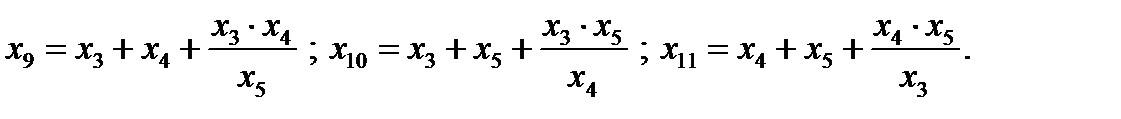Приведение в именованных единицах
Величины, характеризующие элементы электроэнергетической системы, могут быть заданы в относительных единицах или процентах. Для определения этих величин в именованных единицах следует воспользоваться выражениями:
для генераторов:
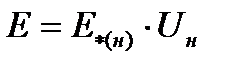 ,
,
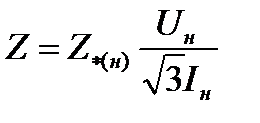 или
или 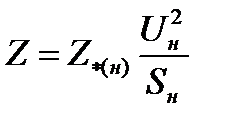 ;
;
где 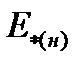 ,
, 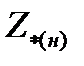 - ЭДС и сопротивление генератора в относительных единицах при номинальных условиях
- ЭДС и сопротивление генератора в относительных единицах при номинальных условиях 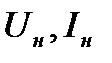 и
и 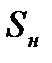 ;
;
для трансформаторов:
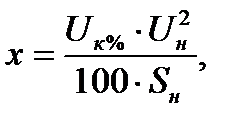
(где 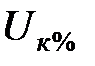 - напряжение короткого замыкания в процентах от номинального);
- напряжение короткого замыкания в процентах от номинального);
для реакторов:
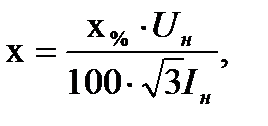
(где 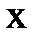 - индуктивное сопротивление, Ом;
- индуктивное сопротивление, Ом; 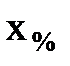 - индуктивное сопротивление, %).
- индуктивное сопротивление, %).
Формулы для определения сопротивлений элементов электроэнергетических систем в именованных единицах даны в табл. 1.
Если для схемы рис.1 за основную (базисную) ступень напряжения принять ступень 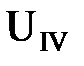 , то ЭДС и сопротивления элементов схемы рис. 1, приведенные к этой ступени, определятся:
, то ЭДС и сопротивления элементов схемы рис. 1, приведенные к этой ступени, определятся:
для генератора как:
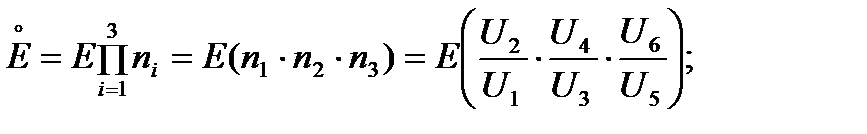
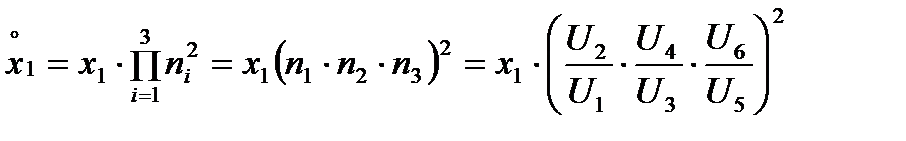 ;
;
для трансформатора Т1:
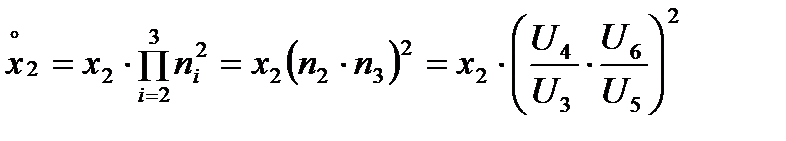 ;
;
для линии Л1:
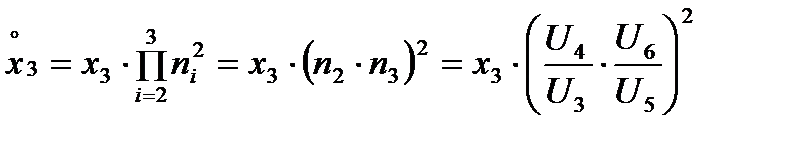 ;
;
для трансформатора Т2:
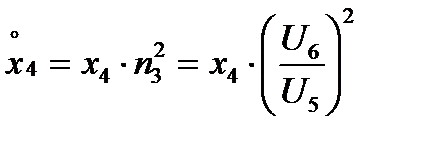 и т.д.
и т.д.
Данное приведение элементов к одной ступени напряжения называется точным, так как выполняется по фактическим (точным) коэффициентам трансформации трансформаторов и автотрансформаторов.
Наряду с точным приведением в практических расчетах часто используется приближенное приведение, упрощающее расчеты. Сущность приближенного приведения элементов к одной ступени напряжения состоит в том, что для каждой ступени напряжения вместо точных значений напряжений элементов схемы устанавливается среднее номинальное напряжение 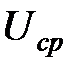 , а именно: 0, 127; 0, 23; 0, 4; 0, 525; 0, 69; 3, 15; 6, 3; 10, 5; 13, 8; 15, 75; 18; 20; 24; 27; 37; 115; 154; 230; 340; 515; 770; 1175 кВ. При этом условно принимают, что номинальные напряжения всех элементов (кроме реакторов), находящихся на одной ступени, одинаковы и равны среднему номинальному напряжению данной ступени. Следовательно, коэффициенты трансформации трансформаторов и автотрансформаторов, как повышающих, так и понижающих, получаются равными отношению средних номинальных напряжений.
, а именно: 0, 127; 0, 23; 0, 4; 0, 525; 0, 69; 3, 15; 6, 3; 10, 5; 13, 8; 15, 75; 18; 20; 24; 27; 37; 115; 154; 230; 340; 515; 770; 1175 кВ. При этом условно принимают, что номинальные напряжения всех элементов (кроме реакторов), находящихся на одной ступени, одинаковы и равны среднему номинальному напряжению данной ступени. Следовательно, коэффициенты трансформации трансформаторов и автотрансформаторов, как повышающих, так и понижающих, получаются равными отношению средних номинальных напряжений.
Если имеется каскад трансформаторов и автотрансформаторов, то результирующий коэффициент трансформации этого каскада будет определяться как отношение Uср крайних ступеней, так как промежуточные коэффициенты сокращаются:
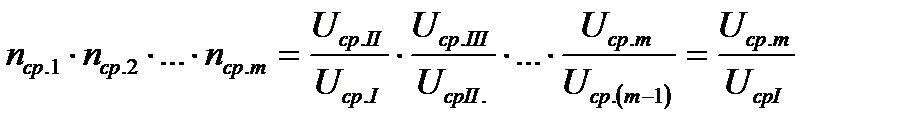 .
.
При приближенном приведении выражения (1-4)для пересчета принимают более простой вид:
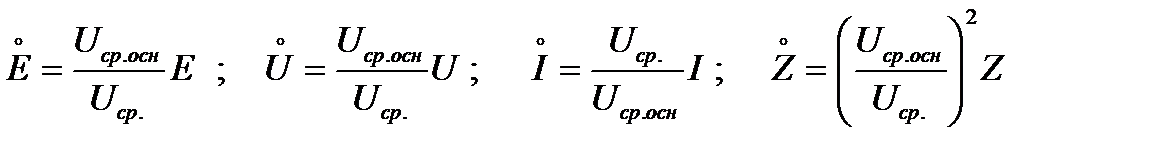 ,
,
(где 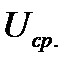 - среднее номинальное напряжение ступени, на котором находятся элементы с подлежащими приведению параметрами, кВ;
- среднее номинальное напряжение ступени, на котором находятся элементы с подлежащими приведению параметрами, кВ; 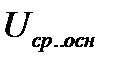 - среднее номинальное напряжение сети той ступени напряжения, которая принята за основную, кВ.
- среднее номинальное напряжение сети той ступени напряжения, которая принята за основную, кВ.
Для схемы рис.1 ЭДС и сопротивления элементов, приведенные к ступени напряжения UIV, принятую за основную, определяются:
для генератора как
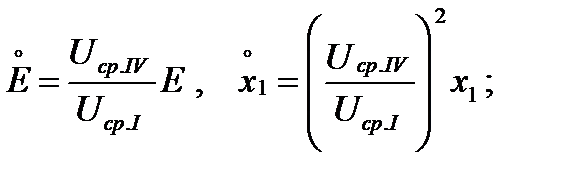
для трансформатора Т1: 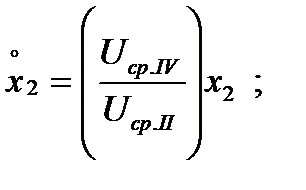 для линии Л1:
для линии Л1: 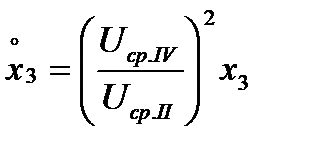 и т.д.
и т.д.
Приближенное приведение вносит погрешность в расчет, поэтому его нужно использовать с некоторой осторожностью. Так, например, при расчетах, связанных с оценкой устойчивости электроэнергетических систем, выбором и настройкой релейной защиты и автоматики, следует пользоваться формулами точного приведения, а при расчетах токов короткого замыкания для выбора электрического оборудования – приближенными.
Приведение в относительных единицах
Электрические величины могут быть выражены в именованных единицах (амперах, вольтах, омах и т.д.) и в относительных (в частности, процентах), т.е. в долях от некоторых именованных величин, называемых в дальнейшем базисными.
Определение результирующего сопротивления в относительных единицах возможно только в том случае, если относительные сопротивления всех элементов цепи вычислены при одних и тех же базисных условиях.
Базисных электрических величин четыре: 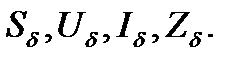 Две любые из этих величин являются независимыми, а две другие определяются из соотношений для трехфазной цепи и закона Ома:
Две любые из этих величин являются независимыми, а две другие определяются из соотношений для трехфазной цепи и закона Ома:
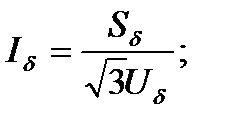
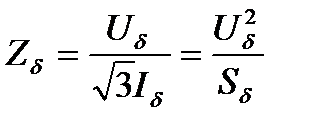 .
.
При расчетах токов короткого замыкания в качестве независимых базисных величин обычно принимают 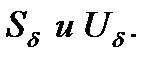 Относительные величины ЭДС, напряжений, токов, мощностей и сопротивлений при выбранных базисных условиях (величинах) определяются как
Относительные величины ЭДС, напряжений, токов, мощностей и сопротивлений при выбранных базисных условиях (величинах) определяются как
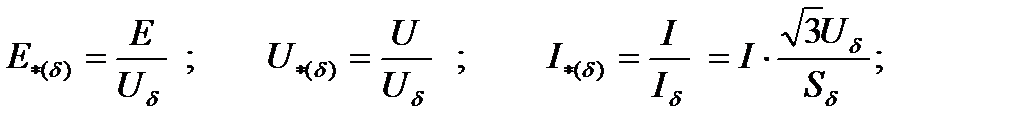
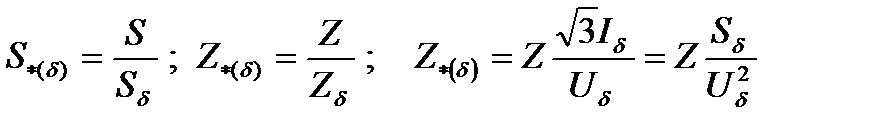 ,
,
где звездочка указывает на то, что величина выражена в относительных единицах, а индекс (d) – что она приведена к базисным условиям.
При выборе базисных величин следует стремиться к упрощению вычислений. Для этого за базисную мощность 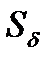 целесообразно принимать круглое число (100 МВ·А, 1000 МВ·А и т.д.), или часто повторяющуюся в данной схеме номинальную мощность (или кратную ей). В качестве базисного напряжения рекомендуется выбирать номинальное напряжение ступени короткого замыкания. Если расчетная схема содержит несколько ступеней напряжения, то параметры всех элементов должны быть приведены к одной ступени, принимаемую за основную, базисную.
целесообразно принимать круглое число (100 МВ·А, 1000 МВ·А и т.д.), или часто повторяющуюся в данной схеме номинальную мощность (или кратную ей). В качестве базисного напряжения рекомендуется выбирать номинальное напряжение ступени короткого замыкания. Если расчетная схема содержит несколько ступеней напряжения, то параметры всех элементов должны быть приведены к одной ступени, принимаемую за основную, базисную.
Для составления схемы замещения в относительных единицах при точном приведении нужно:
1. На одной из ступеней напряжения схемы, выбранной в качестве основной, задать базисные величины 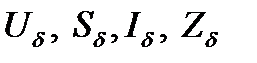 ;
;
2. По формулам:
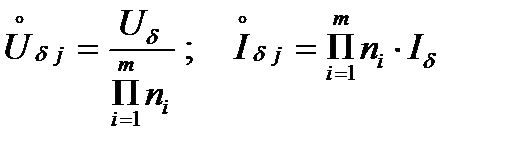 или
или 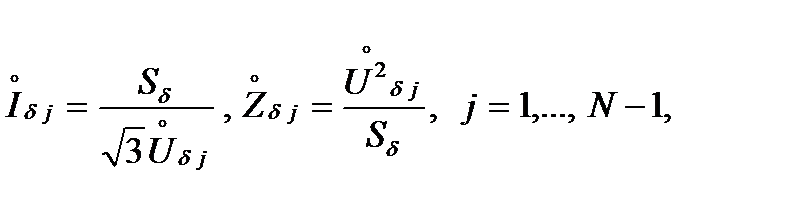 (6)
(6)
определить базисные величины для всех остальных (N-1) ступеней напряжений.
В формулах (6): 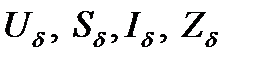 - заданные произвольно базисные величины для ступени напряжения, выбранной в качестве основной;
- заданные произвольно базисные величины для ступени напряжения, выбранной в качестве основной; 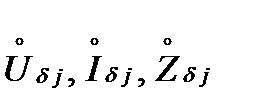 - базисные величины j-той ступени напряжения, приведенные к основной ступени при точном приведении; N-число ступеней напряжения в расчетной схеме.
- базисные величины j-той ступени напряжения, приведенные к основной ступени при точном приведении; N-число ступеней напряжения в расчетной схеме.
3. По формулам (5) подсчитать все величины в относительных единицах при базисных условиях ( 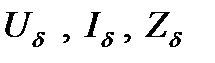 ) той ступени трансформации, на которой находятся подлежащие приведению величины.
) той ступени трансформации, на которой находятся подлежащие приведению величины.
Например, формулы (5) для определения в относительных единицах параметров элементов, находящихся на j-той ступени напряжения запишутся:
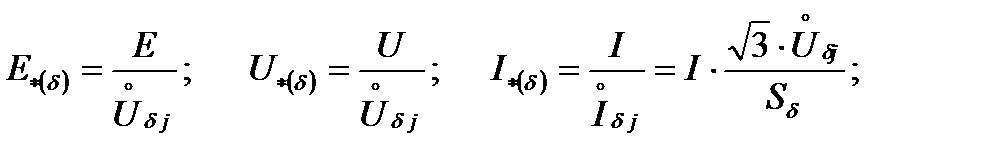
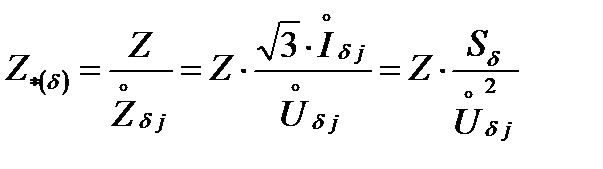 .
.
При приближенном приведении при принятии в качестве величины базисного напряжения для основной ступени среднего номинального напряжения этой ступени, т.е. 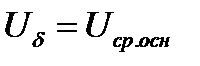 , базисные напряжения остальных ступеней напряжения расчетной схемы будут равны средним номинальным напряжениям этих ступеней, т.е.
, базисные напряжения остальных ступеней напряжения расчетной схемы будут равны средним номинальным напряжениям этих ступеней, т.е. 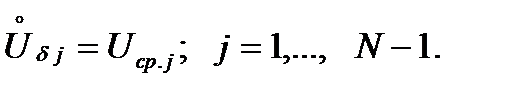
Если ЭДС и сопротивления рассматриваемых элементов (генераторов, трансформаторов, реакторов и др.) заданы в относительных единицах при номинальных условиях, то пересчет их в относительные единицы при базисных условиях следует производить по выражениям:
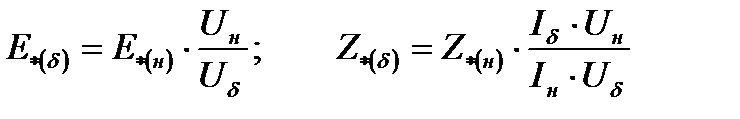 или
или 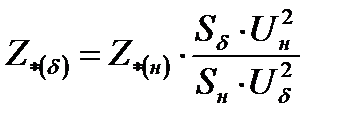 .
.
Формулы для расчета сопротивлений различных элементов в относительных единицах при точном и приближенном приведении даны в табл. 1.
1.2. Преобразование схем замещения
При расчетах токов короткого замыкания, как правило, возникает необходимость в преобразовании исходной схемы к более простому виду. Применение тех или иных методов преобразования зависит, прежде всего, от конфигурации исходной схемы, применяемого метода расчета, интересующих величин и от требований, предъявляемых к расчету.
|
|
|
| Продолжение таблицы 1
|
| Элемент
электрической
системы
| Схема
замещения
| Параметры
элемента
| Формулы для расчета в
|
| именованных
| относительных единицах при
|
| единицах,
Ом
| точном
приведении
| приближенном
приведении
|
| Трансформатор двухобмоточный с рас-щепленной обмоткой низкого напряжения
|
| Uk%, Sн, Uн
| xВ=0;
xн1=xн2= 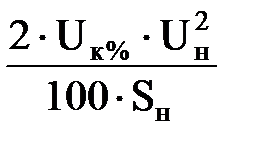 . .
| 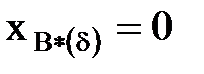 ;
xн1*(d)=xн2*(d)=
= ;
xн1*(d)=xн2*(d)=
= 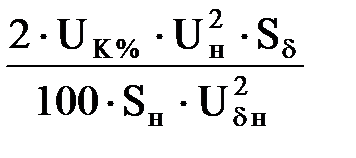 . .
| 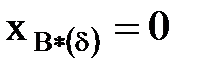 ;
x1*(d)=x2*(d)= ;
x1*(d)=x2*(d)= 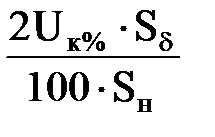 . .
|
| Реактор
|
| xP%, Iн, Uн
| 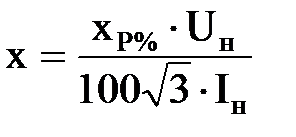 . .
| 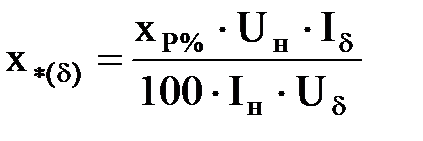 . .
| 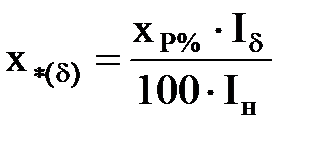 . .
|
| Реактор сдвоенный
|
| xP%, Iн, Uн
| 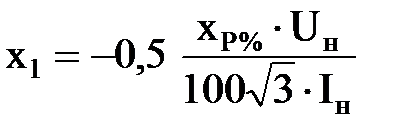 ;
x2= x3=
= ;
x2= x3=
= 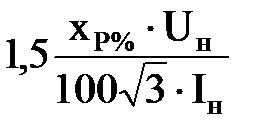 . .
| 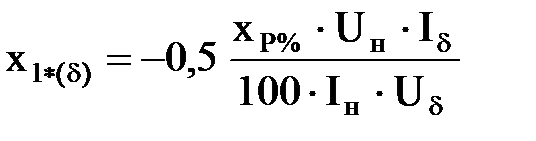 ; x2*(d)= x3*(d)=
= ; x2*(d)= x3*(d)=
= 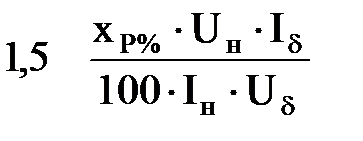 . .
| 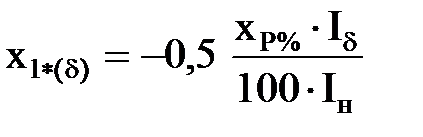 ;
x2*(d)=x3*(d)=
= ;
x2*(d)=x3*(d)=
= 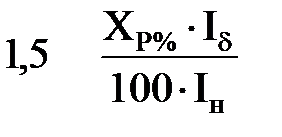 . .
|
| Воздушные линии, кабели
| х
| x0, 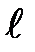 , Uн , Uн
| 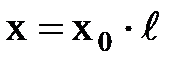 . .
| 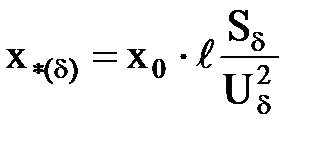 . .
| 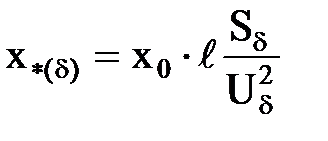 . .
|
| Двигатель
| 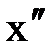
| Sн, Uн, I*пуск
| 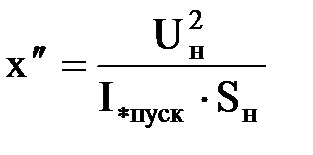 . .
| 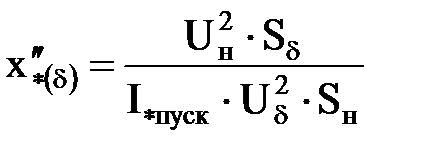 . .
| 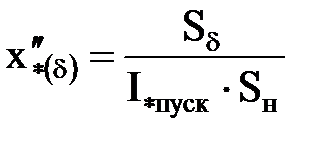 . .
|
Параллельное сложение элементов схемы замещения
Наиболее простым преобразованием является замена нескольких параллельных ветвей (пассивных или активных) одной эквивалентной. Так, если к произвольному узлу схемы (рис.2, а) присоединено любое число генерирующих ветвей с ЭДС 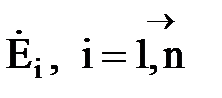 и реактивностями
и реактивностями 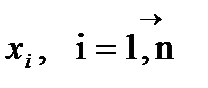 , то все они могут быть заменены одной эквивалентной генерирующей ветвью с результирующей ЭДС
, то все они могут быть заменены одной эквивалентной генерирующей ветвью с результирующей ЭДС 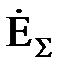 и результирующей реактивностью
и результирующей реактивностью 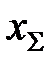 (рис.2, б), определяемыми по формулам
(рис.2, б), определяемыми по формулам
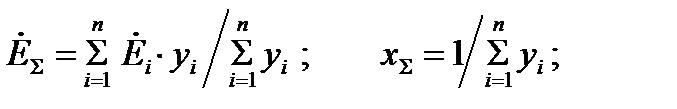
где
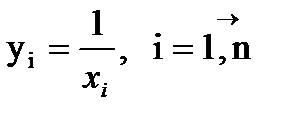
- проводимости заданных ветвей.
Рисунок 2 – Замена генерирующих ветвей (2, а) одной эквивалентной (2, б).
При двух генерирующих ветвях в узле:
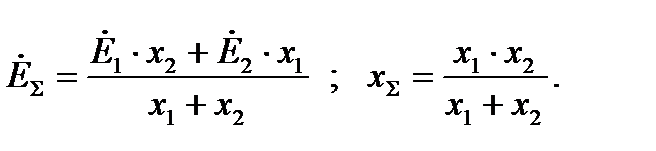
Подобная замена возможна при любых значениях ЭДС. Пассивные ветви и ветви с точкой КЗ можно рассматривать как частные случаи, когда 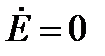 .
.
Задачей расчета токов коротких замыканий обычно является нахождение тока в аварийной ветви или в месте короткого замыкания. Поэтому преобразование схемы удобнее вести так, чтобы аварийная ветвь, по возможности, была сохранена до конца преобразования. С этой целью концы нагрузочных ветвей, ЭДС которых принимаются равными нулю, не следует соединять с точкой короткого замыкания; лучше эти ветви объединить с генераторными в эквивалентные генерирующие ветви.
Преобразование звезды и треугольника сопротивлений
Упрощение схемы можно получить преобразованием треугольника сопротивлений в звезду и звезды - в треугольник.
Схема на рис.3, а принимает вид рис.3, б после замены треугольника сопротивлений 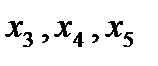 эквивалентной звездой с лучами сопротивлений
эквивалентной звездой с лучами сопротивлений 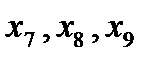 , определяемыми по выражениям:
, определяемыми по выражениям:
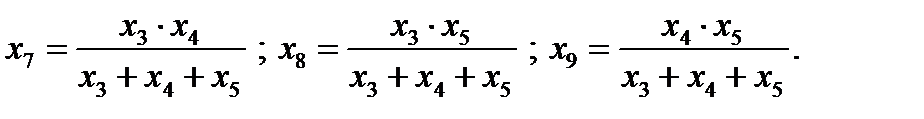
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAJNOHtMIA AADdAAAADwAAAGRycy9kb3ducmV2LnhtbERPzWoCMRC+F/oOYQq91WzttuhqFKkIRXqw6gMMm9nN 4mayJKmmb98Igrf5+H5nvky2F2fyoXOs4HVUgCCune64VXA8bF4mIEJE1tg7JgV/FGC5eHyYY6Xd hX/ovI+tyCEcKlRgYhwqKUNtyGIYuYE4c43zFmOGvpXa4yWH216Oi+JDWuw4Nxgc6NNQfdr/WgXl +p3KnfVvW6O/N13TpPVulZR6fkqrGYhIKd7FN/eXzvPH0xKu3+QT5OIfAAD//wMAUEsBAi0AFAAG AAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQ SwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQ SwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1s LnhtbFBLAQItABQABgAIAAAAIQAk04e0wgAAAN0AAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABAD1AAAAhwMAAAAA "/>
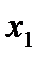
Рисунок 3 – Преобразование треугольника сопротивлений (3, а) в звезду (3, б).
На рис.4, а представлена схема, которая приводится к более простому виду после преобразования звезды с лучами 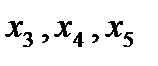 в эквивалентный треугольник со сторонами
в эквивалентный треугольник со сторонами 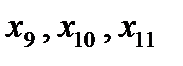 и последующим размыканием полученного треугольника по узлу с ЭДС
и последующим размыканием полученного треугольника по узлу с ЭДС 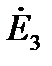 (рис. 4, б).
(рис. 4, б).
Формулы преобразования звезды в эквивалентный треугольник:
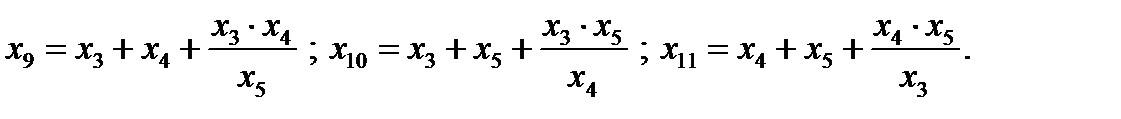
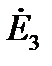
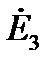
Рисунок 4 – Преобразование трехлучевой звезды в эквивалентный треугольник (4, а) с последующим размыканием по узлу с ЭДС 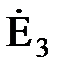 (4, б).
(4, б).
После параллельного сложения ветвей с 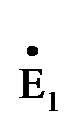 и
и 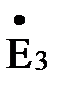 ;
; 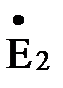 и
и 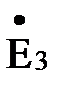 схема рис. 4, б приобретает вид схемы рис. 3 а, преобразование которой к более простому виду рассмотрено выше.
схема рис. 4, б приобретает вид схемы рис. 3 а, преобразование которой к более простому виду рассмотрено выше.
Преобразование многолучевой звезды в многоугольник с диагоналями
При этом преобразовании сопротивление связи между произвольными вершинами m и е многоугольника определяется по формуле
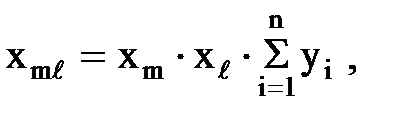
где 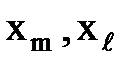 - реактивности лучей звезды, исходящих из точек m ие;
- реактивности лучей звезды, исходящих из точек m ие; 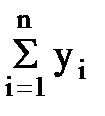 - суммарная проводимость всех лучей преобразуемой звезды;
- суммарная проводимость всех лучей преобразуемой звезды;
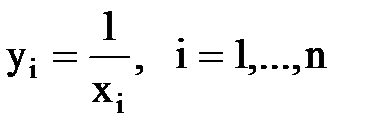
В качестве примера такого преобразования на рис. 5. представлено преобразования четырехлучевой звезды (рис. 5, а) в четырехугольник с диагоналями (рис. 5, б).
Рисунок 5 – Преобразование четырехлучевой звезды в четырехугольник с диагоналями.
Рисунок 6 является иллюстрацией данного способа преобразования схем замещения.
Рисунок 6 – Иллюстрация использования преобразования четырехлучевой звезды в четырехугольник с диагоналями.
Если четырехлучевую звезду с элементами 1, 2, 4, 5, (рис.6, а) заменить четырехугольником 1п, 1f, ne, fe c диагоналями 1е и fn, то после размыкания по узлу с Ė 1 и замены образовавшихся параллельных ветвей эквивалентными (x6//xnℓ ; x8//xfe) схема (рис. 6, б) приобретает уже знакомый вид (рис.4, б).
Выбор кратчайшего пути преобразования достигается практикой решения подобных задач. Очевидные на первый взгляд преобразования не всегда являются наиболее рациональными, так как могут в дальнейшем привести к усложнения схемы и, следовательно, к увеличению вычислительной работы. Поэтому прежде, чем производить вычислительные операции, следует наметить ход предполагаемых преобразований.
1.3. Применение коэффициентов токораспределения для определения взаимных сопротивлений между отдельными источниками питания и точкой короткого замыкания
В практике расчетов токов КЗ часто возникает необходимость в определении взаимных сопротивлений между точкой КЗ и отдельными генераторами (рис. 1). Для этой цели можно использовать коэффициенты токораспределения. Если ток в точке КЗ условно принять за единицу, то, полагая все ЭДС ветвей равными по модулю и фазе, можно найти токи в ветвях схемы в долях от этой единицы. Значения долей тока в каждой ветви называются коэффициентами токораспределения и обозначаются С1, С2, …, Сn.
Рисунок 7 – Схема токораспределения
Следовательно, коэффициент токораспределения любой ветви численно равен току этой ветви, если суммарный ток в точке КЗ равен единице. Таким образом, коэффициенты токораспределения для генераторов характеризуют долю их участия в питании точки КЗ
По коэффициенту токораспределения Сi любого генератора и результирующему сопротивлению схемы относительно точки КЗ 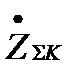 легко найти взаимное сопротивление между этим генератором и точкой КЗ как
легко найти взаимное сопротивление между этим генератором и точкой КЗ как
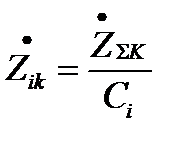 ,
,
где Ż Σ K для примера рис. 1 равно
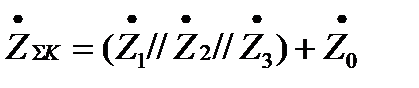 .
.
При помощьи коэффициентов токораспределения схема любой конфигурации довольно просто приводится к многолучевой звезде с вершиной в точке КЗ Общий ток в точке КЗ определяется в данном случае суммой токов отдельных ветвей, в которых учитывается влияние изменения величин и фаз отдельных ЭДС.
Коэффициенты токораспределения используют и тогда, когда необходимо найти величину тока, протекающему по любому элементу схемы к точке КЗ Для этого достаточно найти коэффициент токораспределения для данного элемента Ci и умножить его на суммарный ток в точке КЗ
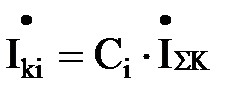 .
.
Популярное:


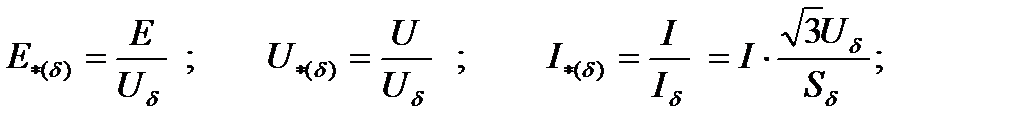
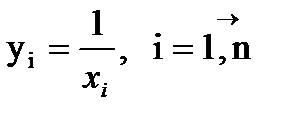 - проводимости заданных ветвей.
- проводимости заданных ветвей.