Раздел 2. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Основные формулы
1. Основное уравнение молекулярно- кинетической теории газов: 
2. Уравнение Клапейрона-Менделеева: 
3. Средняя кинетическая энергия молекулы: 
4. Средняя квадратичная скорость: 

5. Средняя арифметическая скорость: 
6. Наиболее вероятная скорость: 
7. Средняя длина свободного пробега молекул:  =
=  .
.
8. Среднее число соударений одной молекулы за единицу времени:

 =
= 
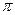 d2
d2 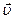 n0.
n0.
9. Распределение молекул в поле силы тяжести (распределение Больцмана): 
10. Барометрическая формула: 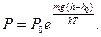
11. Уравнение диффузии: 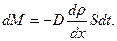
12. Уравнение вязкости: 
13. Уравнение теплопроводности: 
14. Коэффициент диффузии: 
15. Коэффициент внутреннего трения (вязкости): 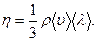
16. Коэффициент теплопроводности: 
17. Уравнение первого закона термодинамики: 
18. Внутренняя энергия идеального газа: 

19. Элементарная работа: 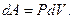
20. Работа при изобарическом процессе: 
21. Работа при изотермическом процессе: 
22. Работа при адиабатическом процессе: 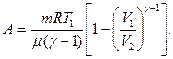
23. Уравнение адиабатического процесса (уравнение Пуассона): 
Т1 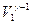 =
=  .
.
24. Коэффициент полезного действия цикла Карно: 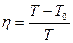 ,
,
где  - соответственно температуры нагревателя и холодильника.
- соответственно температуры нагревателя и холодильника.
25. Уравнение Майера: 
26. Изохорическая молярная теплоемкость: 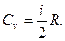
27. Изобарическая молярная теплоемкость: 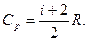
28. Связь между молярными  и
и  и удельными
и удельными 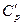 и
и  теплоемкостями газа:
теплоемкостями газа: 

29. Изменение энтропии: 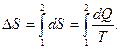
30. Уравнение Ван-дер-Ваальса: 
31. Высота поднятия жидкости в капилляре с радиусом r: 
Примеры решения задач
Задача 1. При какой температуре средняя квадратичная скорость поступательного движения молекул одноатомного газа составляет 830 м/с?
Дано:
< 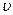 кв> =830 м/с; кв> =830 м/с;
 кг/моль; кг/моль;
 Т -?
Т -?
|  Решение:
Средняя кинетическая энергия молекул
< E> = Решение:
Средняя кинетическая энергия молекул
< E> = 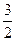 KT, (1)
где К= KT, (1)
где К= 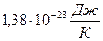 - постоянная Больцмана - постоянная Больцмана
|
< E> = 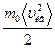 , (2)
mо – масса одной молекулы mо= , (2)
mо – масса одной молекулы mо=  .
Решая (1) и (2) .
Решая (1) и (2)  ; Т= ; Т=  .
Произведем вычисления:
Т= .
Произведем вычисления:
Т=  = 774, 6 К
Ответ: Т = 774, 6 К. = 774, 6 К
Ответ: Т = 774, 6 К.
|
 Задача 2. Сосуд с воздухом, давление которого 97 кПа, соединен с поршневым откачивающим устройством. После пяти ходов поршня давление воздуха в сосуде стало 29 кПа. Определить отношение объемов сосуда и цилиндра откачивающего устройства.
Задача 2. Сосуд с воздухом, давление которого 97 кПа, соединен с поршневым откачивающим устройством. После пяти ходов поршня давление воздуха в сосуде стало 29 кПа. Определить отношение объемов сосуда и цилиндра откачивающего устройства.
Дано:
р0 = 97 кПа = 9, 7 ∙ 104 Па;
р5 = 29 кПа = 2, 9∙ 104 Па;
 n = 5 м.
V1/V2 -? n = 5 м.
V1/V2 -?
| Решение:
Пусть V1 и V2 – объемы сосуда и цилиндра откачивающего устройства. После первого соединения цилиндра с сосудом по закону Бойля - Мариотта имеем р0V1 = p1(V1 + V2), откуда р1 = р0V1 / (V1+V2).
После второго соединения р1V1 = p2(V1 + V2),
|
Откуда р2 = p1V1/(V1 + V2), или р2 = p0V12/(V1+V2)2.
Аналогично, после пятого соединения р5 = p0V15/(V1 + V2)5.
Преобразуем полученное выражение:
 (V1+V2)/V1 = 1, 272, откуда V1/V2 = 3, 68.
Ответ: V1/V2 = 3, 68.
(V1+V2)/V1 = 1, 272, откуда V1/V2 = 3, 68.
Ответ: V1/V2 = 3, 68.
|
Задача 3. В баллоне содержится смесь азота количеством вещества 5 моль и водорода количеством вещества 10 моль при температуре 7 0С и давлении 2, 5 МПа. Определить плотность смеси.
Дано:
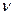 1=5 моль; 1=5 моль;
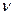 2=10 моль; 2=10 моль;
 = = 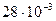 кг/моль; кг/моль;  = =  кг/моль; R=8, 31 Дж/(моль.К); рсм=2, 5 Мпа=2, 5.106 Па; Т= 7 0С + 273 0С = 280 К кг/моль; R=8, 31 Дж/(моль.К); рсм=2, 5 Мпа=2, 5.106 Па; Т= 7 0С + 273 0С = 280 К
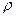  -? -?
|  Решение:
На основании определения плотности как физической величины для данного случая имеем: Решение:
На основании определения плотности как физической величины для данного случая имеем:
 , (1)
где m1 и m2 – массы азота и водорода соответственно; V – объем баллона.
Выразим массу азота и водорода через количество вещества и молярную массу: , (1)
где m1 и m2 – массы азота и водорода соответственно; V – объем баллона.
Выразим массу азота и водорода через количество вещества и молярную массу:
 ; ;  . (2) . (2)
|
Для определения объема газа в баллоне воспользуемся уравнением Менделеева – Клапейрона для смеси газов: 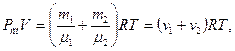 где R – универсальная (молярная) газовая постоянная; Т – термодинамическая температура.
Отсюда найдем:
где R – универсальная (молярная) газовая постоянная; Т – термодинамическая температура.
Отсюда найдем:
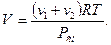 (3)
Подставив выражения m1 и m2 по (2) и V по (3) в (1), получим: (3)
Подставив выражения m1 и m2 по (2) и V по (3) в (1), получим:
 (4)
Вычислим: (4)
Вычислим:
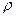 = =  кг/м3 = 11, 5 кг/м3.
Ответ: р =11, 5 кг/м3. кг/м3 = 11, 5 кг/м3.
Ответ: р =11, 5 кг/м3.
|
Задача 4. Определить внутреннюю энергию водяного пара массой 180 г, принимая его за идеальный газ при температуре -73 °С, а также кинетическую энергию вращательного движения одной молекулы пара при той же температуре.
 Дано:
m=180 г = 0, 18 кг; Дано:
m=180 г = 0, 18 кг;
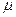 =18.10-3 кг/моль;
Т=200 К. =18.10-3 кг/моль;
Т=200 К.
 U -?
U -? 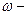 ? ?
| Решение:
Внутренняя энергия идеального газа есть полная кинетическая энергия всех молекул газа и выражается формулой:
U =  , (1) , (1)
|
где i = 6 – число степеней свободы молекулы газа;
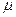 - молярная масса;
R – универсальная (молярная) газовая постоянная;
Т – абсолютная температура газа. - молярная масса;
R – универсальная (молярная) газовая постоянная;
Т – абсолютная температура газа.
|
Подставим числовые данные в формулу (1) и вычислим:
U =  Дж = 4, 99.104 Дж = 49, 9 кДж.
Известно, что на каждую степень свободы молекулы газа приходится одинаковая энергия, выраженная формулой: Дж = 4, 99.104 Дж = 49, 9 кДж.
Известно, что на каждую степень свободы молекулы газа приходится одинаковая энергия, выраженная формулой:
 , (2)
где , (2)
где 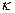 - постоянная Больцмана; Т – абсолютная температура газа. Так как вращательному движению трехатомной молекулы соответствуют три степени свободы, то энергия вращательного движения молекулы водяного пара определяется выражением: - постоянная Больцмана; Т – абсолютная температура газа. Так как вращательному движению трехатомной молекулы соответствуют три степени свободы, то энергия вращательного движения молекулы водяного пара определяется выражением:
 . (3)
Подставив в формулу (3) значение . (3)
Подставив в формулу (3) значение 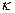 =1, 38.10-23 Дж/К и Т=200 К, получим: =1, 38.10-23 Дж/К и Т=200 К, получим:
 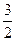 .1, 38.10-23.200 Дж = 4, 14.10-21 Дж.
Ответ: U = 49, 9 кДж; .1, 38.10-23.200 Дж = 4, 14.10-21 Дж.
Ответ: U = 49, 9 кДж;  4, 14.10-21 Дж. 4, 14.10-21 Дж.
|
Задача 5. Кислород массой 320 г изобарически расширяется при давлении 2.105 Па. Температура газа изменяется от 20 оС до некоторого значения t2. Определить работу А, совершенную газом при расширении, и конечный объем V2 газа, если на расширение затрачена теплота 10 кДж.
Дано:
m=320 г = 0, 32 кг;
р=2.105 Па;
t1=20 0С;
Q = 10 кДж=107Дж.
 А-? V2-? А-? V2-?
|  Решение:
Для вычисления работы газа воспользуемся формулой:
А= Решение:
Для вычисления работы газа воспользуемся формулой:
А=  R(T2 - T1), (1)
где R(T2 - T1), (1)
где 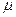 - молярная масса кислорода; R – универсальная - молярная масса кислорода; R – универсальная
|
(молярная) газовая постоянная; Т1 и Т2 – начальная и конечная температуры газа. Т1= t1 0C + 237 0C = 290 К.
Неизвестная разность температур может быть выражена из формулы:
Q = cp m(T2 – T1), (2)
где ср – удельная теплоемкость при постоянном давлении,:
ср =  ; i = 5.
Т2 – Т1 = ; i = 5.
Т2 – Т1 =  . (3)
Подставив это выражение разности температур в (1), получим:
А = . (3)
Подставив это выражение разности температур в (1), получим:
А =  (4) (4)
|
Вычислим: А = 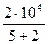 Дж = 2, 86.103 Дж = 2, 86 кДж.
Для вычисления конечного объема V2 воспользуемся иным выражением для работы газа в изобарическом процессе:
А = Дж = 2, 86.103 Дж = 2, 86 кДж.
Для вычисления конечного объема V2 воспользуемся иным выражением для работы газа в изобарическом процессе:
А =  (V2 – V1), (5)
где V1 и V2 – начальный и конечный объем газа.
Отсюда
V2 = (V2 – V1), (5)
где V1 и V2 – начальный и конечный объем газа.
Отсюда
V2 =  (A + (A +  V1). (6)
Второе слагаемое в скобках, содержащее неизвестную величину V1, можем определить, воспользовавшись уравнением Менделеева – Клапейрона для начального состояния газа: V1). (6)
Второе слагаемое в скобках, содержащее неизвестную величину V1, можем определить, воспользовавшись уравнением Менделеева – Клапейрона для начального состояния газа:
 V1 = V1 =  RT1. (7)
Подставив выражение (7) в (6), получим: RT1. (7)
Подставив выражение (7) в (6), получим:
 V2 =
V2 =  м3 = 0, 136 м3 = 136 л.
Ответ: А =2, 86 кДж; V2 =136 л. м3 = 0, 136 м3 = 136 л.
Ответ: А =2, 86 кДж; V2 =136 л.
|
Задача 6. Определить: 1) среднюю длину свободного побега молекул воздуха при температуре 0 0С и давлении 1, 01 Па; 2) среднее число столкновений молекул. Принять диаметр молекулы воздуха 2, 9.10-8 см.
 Дано:
T=273 К;
р=1, 01 Па;
d =2, 9.10-8 см = 2, 9× 10-10м. Дано:
T=273 К;
р=1, 01 Па;
d =2, 9.10-8 см = 2, 9× 10-10м.
  -? -?  -? -?
| Решение:
Средняя длина свободного пробега молекул определяется формулой:
 , (1)
где d – диаметр молекулы; n – концентрация молекул (число молекул в единице объема газа). , (1)
где d – диаметр молекулы; n – концентрация молекул (число молекул в единице объема газа).
|
Для определения 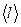 используем соотношение
n = используем соотношение
n =  , (2)
где р – давление газа; Т – температура газа; k – постоянная Больцмана.
Подставив выражение n из (2) в (1), получим , (2)
где р – давление газа; Т – температура газа; k – постоянная Больцмана.
Подставив выражение n из (2) в (1), получим
 . (3)
Вычислим: . (3)
Вычислим:  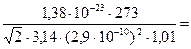 10-2 м=1см.
Среднее число столкновений молекул газа связано с длиной свободного пробега соотношением: 10-2 м=1см.
Среднее число столкновений молекул газа связано с длиной свободного пробега соотношением:
 , (4) , (4)
|
где  - средняя арифметическая скорость молекул. Ее можно определить по формуле: - средняя арифметическая скорость молекул. Ее можно определить по формуле:
 = = 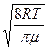 , (5)
где R – универсальная газовая постоянная; , (5)
где R – универсальная газовая постоянная; 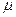 – молярная масса воздуха. Подставим выражение – молярная масса воздуха. Подставим выражение  из (5) в (4) и, сделав соответствующие преобразования, получим: из (5) в (4) и, сделав соответствующие преобразования, получим:
 . (6)
Подставим числовые значения в (6) и вычислим: . (6)
Подставим числовые значения в (6) и вычислим:
 с-1 = 4, 46.103 с-1.
Ответ: с-1 = 4, 46.103 с-1.
Ответ:  =1 см; =1 см;  =4, 46.103 с-1. =4, 46.103 с-1.
|
Задача 7. Плотность газа 0, 2 кг/м3, давление 1, 01.104 Па. Определить при этих условиях среднюю квадратичную скорость молекул газа.
 Дано: Дано:
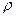 =0, 2 кг/м3; Р=1, 01.104 Па. =0, 2 кг/м3; Р=1, 01.104 Па.

 -? -?
| Решение:
Средняя квадратичная скорость определяется по формуле:
   , (1) , (1)
|
где R – универсальная (молярная) газовая постоянная;
Т – абсолютная температура газа; 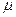 - молярная масса.
Для определения неизвестных величин Т и - молярная масса.
Для определения неизвестных величин Т и 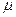 используем уравнение Менделеева – Клапейрона: РV = используем уравнение Менделеева – Клапейрона: РV =  RT. Отсюда: RT. Отсюда:
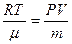 или или
 , (2)
где , (2)
где 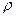 - плотность газа. - плотность газа.
|
Подставив значение  из (2) в (1), найдем: из (2) в (1), найдем:
  . (3)
Вычислим: . (3)
Вычислим:  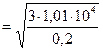 м/с = 389 м/с.
Ответ: м/с = 389 м/с.
Ответ:  = 389 м/с. = 389 м/с.
|
Задача 8. Определить время, в течение которого через поверхность площадью 1 м2 продиффундирует воздух массой 720 мг из почвы в атмосферу, если принять коэффициент диффузии воздуха, градиент плотности: 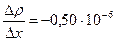 г/см4 .
г/см4 .
Дано:
S =1 м2;
m=720мг =7, 2× 10-4кг
D=0, 04 см2/с=4.10-6 м2/с;
 = - 0, 50.10-6 г/см4 = = - 0, 50.10-6 г/см4 =
 = - 0, 05 кг/м4.
t =? = - 0, 05 кг/м4.
t =?
|  Решение:
Масса газа, перенесенная в результате диффузии, выражается формулой Фика:
m = - D Решение:
Масса газа, перенесенная в результате диффузии, выражается формулой Фика:
m = - D  St, (1)
где D – коэффициент диффузии; St, (1)
где D – коэффициент диффузии;  - градиент плотности, т.е. изменение плотности, приходящееся на единицу глубины слоя почвы; S – площадь - градиент плотности, т.е. изменение плотности, приходящееся на единицу глубины слоя почвы; S – площадь
|
поверхности почвы; t – длительность диффузии.
Из (1) найдем:
t = -  . (2)
Вычислим длительность диффузии:
t = - . (2)
Вычислим длительность диффузии:
t = -  c = 3, 60.103 с = 1 ч.
Ответ: t =1 ч. c = 3, 60.103 с = 1 ч.
Ответ: t =1 ч.
|
Задача 9. Внутренняя поверхность бетонной стены имеет температуру 20 0C, а наружная -10 0C. Толщина стены 25 см. Сколько теплоты проходит через 1 м2 поверхности стены за 1 мин?
Дано:
T1=293 K;
T2= 263 K;
t =1мин =60с;
S =1 м2;
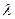 = 0, 817 Дж/(м.с.К); = 0, 817 Дж/(м.с.К);
 x =25 см =0, 25м. x =25 см =0, 25м.
 Q -? Q -?
|  Решение:
Искомую теплоту определим по формуле закона Фурье:
Q = - Решение:
Искомую теплоту определим по формуле закона Фурье:
Q = -  , (1)
где , (1)
где 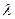 - коэффициент теплопроводности; - коэффициент теплопроводности;  - градиент температуры, т.е. изменение температуры, приходящееся на единицу толщины стены; t – время прохождения теплоты через стену; S – площадь поверхности стены. - градиент температуры, т.е. изменение температуры, приходящееся на единицу толщины стены; t – время прохождения теплоты через стену; S – площадь поверхности стены.
|
Вычислим: Q = 0, 187  .1.60 Дж = 5, 88.103 Дж = 5, 88 кДж
Ответ: Q =5, 88 кДж. .1.60 Дж = 5, 88.103 Дж = 5, 88 кДж
Ответ: Q =5, 88 кДж.
|
Задача 10. Воздух, взятый при температуре 0 0С, был адиабатически сжат так, что его объем уменьшился в три раза. Определить температуру воздуха после сжатия.
 Дано: Дано:
 T1=273 K;
V2=1/3× V1.
Т2-? T1=273 K;
V2=1/3× V1.
Т2-?
| Решение:
Зависимость между температурой и объемом при адиабатном сжатии выражается уравнением Пуассона: Т1 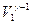 = =  , (1)
где Т1, V1 – соответственно абсолютная температура и , (1)
где Т1, V1 – соответственно абсолютная температура и
|
объем до сжатия воздуха; Т2, V2 – те же величины после сжатия воздуха;  = =  - отношение теплоемкости газа при постоянном давлении Ср к теплоемкости газа при постоянном объеме Сv.
Из теории теплоемкостей газов известно, что - отношение теплоемкости газа при постоянном давлении Ср к теплоемкости газа при постоянном объеме Сv.
Из теории теплоемкостей газов известно, что
 = =  = =  ,
где i – число степеней свободы молекулы газа. Так как воздух – газ двухатомный, то i = 5 и, следовательно: ,
где i – число степеней свободы молекулы газа. Так как воздух – газ двухатомный, то i = 5 и, следовательно:
 = =  = 1, 4.
Из формулы (1) получим: Т2 = Т1 = 1, 4.
Из формулы (1) получим: Т2 = Т1  .
Подставим числовые значения Т=273 К, .
Подставим числовые значения Т=273 К,  =1, 4, V1/V2=3 и вычислим
Т2 =273.31, 4-1 К =273.30, 4 К.
Прологарифмуем обе части полученного равенства:
lgТ2 = lg 273 + 0, 4 lg3 = 2, 436 + 0, 4.0, 477 = 2, 6268.
Т2=424 К.
Ответ: Т2=424 К. =1, 4, V1/V2=3 и вычислим
Т2 =273.31, 4-1 К =273.30, 4 К.
Прологарифмуем обе части полученного равенства:
lgТ2 = lg 273 + 0, 4 lg3 = 2, 436 + 0, 4.0, 477 = 2, 6268.
Т2=424 К.
Ответ: Т2=424 К.
|
Задача 11. Идеальная тепловая машина получает от нагревателя, температура которого 500 К, за один цикл 3360 Дж теплоты. Найти количество теплоты, отдаваемое за один цикл холодильнику, температура которого 400К. Найти работу машины за один цикл.
Популярное:

