
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Элементы учения о строении веществаСтр 1 из 5Следующая ⇒
Особенности поведения микрочастиц. Принципы описания поведения микрочастиц, волновая функция, соотношение неопределенностей, волна де Бройля. Постулаты Бора. Уравнение Шредингера (временное и стационарное), физический смысл входящих в него членов. Решение стационарного уравнения Шредингера для частицы в одномерном потенциальном ящике и частицы на окружности. Условия появления квантовых явлений. Влияние массы и области локализации частиц. Двумерная потенциальная яма, вырождение квантовых состояний и снятие вырождения. Потенциальная яма конечной глубины и влияние ее глубины и ширины на уровни энергии частицы. Возможность локализации частицы в пространстве. Туннельный эффект. Заполнение уровней и принцип Паули, полная энергия совокупности электронов в квантовой системе. Уровни энергии в атоме водорода, переходы между уровнями. Индивидуальность спектров атомов и эмиссионный спектральный анализ. Металлическая модель молекулы и объяснение корреляции цветности вещества и эффекта сопряжения химических связей в молекулах. Нормальная и инверсная заселенность квантовых состояний. Поглощение, спонтанное и вынужденное излучения. Коэффициенты Эйнштейна. Формула Планка. Усиление света при прохождении через инверсно заселенную среду. Понятие о лазерах. Физическая природа химической связи. Электронное строение многоэлектронных атомов, гибридизация, объяснение причин появления пространственных форм молекул. Принцип максимального перекрывания. Внутреннее вращение в молекулах и его роль в биохимических реакциях. Движение частиц в многоатомных молекулах и виды молекулярной спектроскопии. Симметрия молекул и появление правил отбора. Фотохимические реакции и особенности потенциальных поверхностей основных и возбужденных электронных состояний в молекулах. Распад молекул при фотовозбуждениях. Физическая природа фотосинтеза. Транспорт энергии при фотосинтезе. Зонная структура электронных состояний кристаллов. Заполненные и незаполненные зоны. Уровень Ферми. Проводники, полупроводники и диэлектрики. Особенность проводимости в полупроводниках. Систематика элементарных частиц. Законы взаимопревращений частиц, ядерные реакции, дефект массы. Строение ядер, ядерные силы, устойчивые и неустойчивые ядра, естественная и искусственная радиоактивность. Законы радиоактивного распада. Принципы радиоактивационного анализа. «Меченные» атомы в биологии. Пути использования ядерной энергии.
Основные формулы
1. Мгновенная скорость: 2. Мгновенное ускорение: 3. Тангенциальное и нормальное ускорения: 4. Полное ускорение: 5. Уравнения равнопеременного движения: 6. Второй закон Ньютона: 7. Работа переменной силы F на пути S: 8. Мощность: 9. Кинетическая энергия тела: 10. Потенциальная энергия: 11. Закон сохранения механической энергии в консервативных системах:
12. Закон сохранения импульса (количества движения) изолированной системы: 13. Сила трения скольжения: Fтр=mFn. 14. Сила упругости: 15. Потенциальная энергия упругого деформированного тела: 16. Угловая скорость: при равномерном вращении: 17. Угловое ускорение: 18. Соотношение между угловой и линейной скоростями: 19. Уравнение равнопеременного вращательного движения:
20. Момент инерции материальной точки:
21. Моменты инерции различных однородных тел относительно оси, проходящей через центр масс:
совпадающей с геометрической осью цилиндра);
проходящей перпендикулярно стержню через его середину. 22. Момент силы: 23. Основной закон динамики вращательного движения:
24. Закон сохранения момента импульса для изолированной системы:
25. Кинетическая энергия вращающегося тела: 26. Уравнение гармонического колебания: 27. Циклическая частота: 28. Скорость при гармоническом колебательном движении:
29. Ускорение при гармоническом колебательном движении:
30. Полная энергия при гармоническом колебании: 31. Уравнение неразрывности струи в установившемся потоке: (S - сечение трубки тока, 32. Уравнение Бернулли:
Примеры решения задач Задача 1. Поезд отошел от станции и в течение 20 с двигался равноускоренно. Найдите путь, пройденный поездом за 20 с, если известно, что за десятую секунду он прошел путь 5 м.
Задача 3. С вертолета, летящего горизонтально на высоте 125 м со скоростью 25 м/с, бросили груз. На какой высоте скорость груза будет направлена под углом 60о к горизонту?
Задача 4. Из орудия, ствол которого наклонен под углом 600 к горизонту, вылетает снаряд со скоростью 400 м/с. Определить скорость снаряда и его высоту через 4 с после выстрела.
Задача 5. Зависимость пройденного телом пути s от времени t дается уравнением
Задача 6. Камень брошен горизонтально со скоростью 10 м/с. Найти радиус кривизны траектории камня через время 3 c после начала движения.
Задача 7. Точка движется по окружности радиусом 2см. Зависимость пути от времени дается уравнением
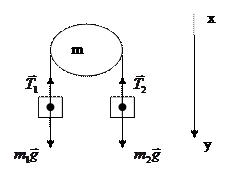
      Задача 8. Две гири с массами 2 кг и 1 кг соединены нитью, перекинутой через блок массой 1 кг. Найти ускорение, с которым движутся гири, и силы натяжения Задача 8. Две гири с массами 2 кг и 1 кг соединены нитью, перекинутой через блок массой 1 кг. Найти ускорение, с которым движутся гири, и силы натяжения 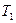 и и 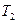 нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь. нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.
Рис. 4
Задача 9. Горизонтальная платформа массой
Задача 11. В небольшой шар массой М, подвешенный на невесомой нерастяжимой нити длиной l, попадает пуля массой m, летящая со скоростью V0 под углом α к горизонту и застревает в шаре. Определить, на какой максимальный угол отклонится нить с шаром от вертикали?
Задача 12. Материальная точка массой 20 г совершает гармонические колебания с периодом 9 с. Начальная фаза колебаний 10°. Через сколько времени от начала движения смещение точки достигнет половины амплитуды? Найти амплитуду, максимальные скорость и ускорение точки, если полная энергия ее равна 0, 001 Дж.
Задача 13. Ареометр массы 55 г, плавающий в растворе серной кислоты, указывает, что плотность жидкости 1, 27 г/см3. Если прибор сместить из положения его равновесия немного по вертикали и отпустить, он начнет колебаться. Считая колебания незатухающими, определить период колебаний. Радиус трубки ареометра, в которой заключена его шкала, равен 0, 30 см. Популярное:
|
Последнее изменение этой страницы: 2016-06-04; Просмотров: 476; Нарушение авторского права страницы