В ЗАДАННОМ БАЗИСЕ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ

⇐ ПредыдущаяСтр 5 из 9Следующая ⇒

2.3.1. Основные теоретические положения. Комбинационными устройствами или автоматами без памяти называют логические устройства, выходной сигнал которых однозначно определяется только действующей в настоящий момент комбинацией входных переменных и не зависит от значений переменных, действовавших на входе в предыдущие моменты времени.

Наиболее часто для описания алгоритма функционирования комбинационных логических устройств используют таблицы истинности или функции алгебры логики.

Таблица, содержащая все возможные комбинации входных переменных и соответствующие им значения выходных переменных, называется таблицей истинности или комбинационной таблицей. Для устройства, имеющего п входов и m выходов, таблица истинности содержит 2ⁿ строк и n + m столбцов.

Зависимость выходных переменных F(X), выраженная через совокупность входных переменных Х₍_n_-1)….Х₀ с помощью операций алгебры логики, носит название функции алгебры логики (ФАЛ).

Логическое произведение входных переменных произвольной строки таблицы истинности, для которой ФАЛ равна единице, называют конституентой единицы. Так как выходной сигнал комбинационного логического устройства может принимать только два значения («лог. 0» или «лог. 1»), то задать алгоритм устройства можно перечислением конституент единицы. Рассмотрим использование таблицы истинности для получения ФАЛ логического устройства.

2.3.2. Получение совершенной дизъюнктивной (CДНФ) и совершенной конъюнктивной (СКНФ) нормальных форм записи ФАЛ. Совершенной дизъюнктивной нормальной формой записи ФАЛ называют логическую сумму (операция ИЛИ) логических произведений (операция И) входных переменных, в каждое из которых аргумент или его отрицание входят один раз. СДНФ легко записывается на основе таблицы истинности с использованием следующего алгоритма:

Комбинационная таблица

X₂	X₁	X₀	F(Х)

для каждого набора переменных, на котором ФАЛ равна единице (для каждой конституенты единицы), записывают логическое произведение входных переменных, причем переменные, равные нулю, записывают с инверсией;

· логически суммируют полученные произведения.

Пример 2.3.1. Записать СДНФ для ФАЛ, заданной таблицей истинности,

Фактически СДНФ это логическая сумма конституент единицы, заданной ФАЛ.

Совершенной конъюнктивной нормальной формой записи ФАЛ называют логическое произведение (операция И) элементарных логических сумм (операция ИЛИ) входных переменных, в каждую из которых аргумент или его инверсия входят один раз. СКНФ легко записывается на основе таблицы истинности с использованием следующего алгоритма:

· для каждого набора переменных, на котором ФАЛ равна нулю (для каждой конституенты нуля), записывают логическую сумму входных переменных, причем переменные, равные единице, записывают с инверсией;

· логически перемножают полученные суммы.

Пример 2.3.2. Записать СКНФ для ФАЛ, заданной таблицей истинности на предыдущей странице,

2.3.3. Минимизация ФАЛ. При увеличении числа переменных, ФАЛ в виде CДНФ или СКНФ достаточно громоздки и их практическая реализация сопряжена со значительными затратами материальных ресурсов. Поэтому, на практике, ФАЛ минимизируют. Целью минимизации является сокращение числа членов исходного выражения. Существует большое число различных методов минимизации, но все они, фактически, базируются на использовании основных теорем алгебры логики:

При большом числе переменных для минимизации ФАЛ используется специальное программное обеспечение. При небольшом числе переменных (не более 5) хорошие результаты дают табличные методы, не требующие привлечения ЭВМ.

Рассмотрим один из этих методов – метод карт Вейча. Данный метод предполагает использование специальных прямоугольных таблиц, построенных на основе таблиц истинности. Для описания этого метода введем понятие соседних кодов.

Соседними называют коды, отличающиеся только в одном разряде. Карты Вейча строятся следующим образом: каждой клетке таблицы ставится в соответствие определенный набор входных переменных (код), причем коды рядом расположенных клеток являются соседними, а в саму таблицу вносятся значения выходного сигнала для заданного набора переменных.

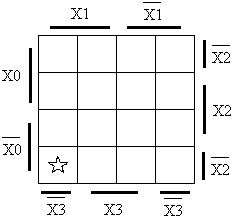
Рис. 2.3.1. Карты Вейча для функций двух, трех и четырех переменных

а) б) в)

Рассмотрим метод заполнения карт Вейча для двух, трех и четырех переменных (для двух, трех и четырех переменных). Искомый код определяется пересечением строк и столбцов, озаглавленных соответствующими переменными. Например, для таблицы, показанной на рис. 2.3.1а, верхняя левая клетка (отмеченная звездочкой) соответствует коду

. Для таблицы, показанной на рис. 2.3.1б, нижняя правая клетка (отмеченная звездочкой) соответствует коду

. Для рисунка 2.3.1в нижняя левая клетка (отмеченная звездочкой) соответствует коду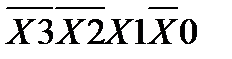

В качестве примера рассмотрим минимизацию ФАЛ, описанной выше в таблице истинности. Заполненная карта Вейча, соответствующая данной таблице, приведена на рис. 2.3.2. При минимизации ФАЛ можно использовать либо ее единичные, либо нулевые значения. При объединении единичных значений ФАЛ получают выражение для самой функции, а при объединении нулевых значении – выражение для функции, инверсной исходной функции.

Минимизация ФАЛ выполняется по следующему алгоритму:

· на карте Вейча ФАЛ выделяют прямоугольные области, объединяющие клетки с выбранным значением функции «лог 1» или «лог. 0». Каждая область должна содержать 2^k клеток, где k - целое число (0, 1, 2, 4, 8, …). Выделенные области могут пересекаться, т. е. одна клетка может входить в несколько различных областей;

· каждая из выделенных областей описывается произведением переменных, которые для этой области остаются неизменными. Каждое произведение должно содержать n – k переменных;

· из полученного множества выбирают минимальное число максимально больших областей, включающих все клетки с выбранным значением ФАЛ;

· логически суммируют выбранные произведения.

Полученное выражение является минимальной дизъюнктивной ФАЛ.

Рис. 2.3.2. Карта Вейча для заданной функции

Рис. 2.3.3. Выделенные области карты Вейча для единичных значений ФАЛ

Воспользуемся приведенной методикой для минимизации вышеприведенной функции. Произведем объединение областей с единичными значениями функции. Имеем три области (см. рис. 2.3.3). Для области I неизменными остаются переменные X1 и X0. Для области II - постоянны переменные Х2 и Х0. Для области III – неизменны Х2 и Х1. Суммируя произведения неизменных переменных для каждой из выделенных областей, получим минимальную дизъюнктивную форму искомой ФАЛ в виде:

В правильности полученной ФАЛ можно убедиться, подставляя в неё различные комбинации входных переменных. Например, для входного кода 001 имеем ¸ что соответствует приведенной таблице истинности.

Объединяя клетки, содержащие нулевые значения функции, так же получим три области. Это область I, для которой неизменны переменные и , область II для которой неизменны и и область III с неизменными и . Суммируя произведения переменных для каждой области, получим ФАЛ, инверсную заданной:

Подставив, для проверки, в полученную ФАЛ входной код 001 найдем:

или F(X) = 0.

Рис. 2.3.4. Выделенные области карты Вейча для нулевых значений ФАЛ

Рис. 2.3.5. Объёмное представление Карты Вейча функции 3-х переменных

Интересно отметить, что в рассмотренном примере область II была получена объединением клеток, расположенных на противоположных краях таблицы. Это следует из основного правила построения таблицы. Коды рядом расположенных клеток должны быть соседними, т.е. отличаться только в одном разряде. Нижней правой клетке рассматриваемой таблицы соответствует код 000, а левой нижней клетке – код 010, т.е. они соседние. Поэтому реально рассматриваемая таблица является объемной фигурой и представляет собой поверхность цилиндра (рис. 2.3.5).

Описание:

Рис. 2.3.6. Возможные варианты объединения ячеек в области

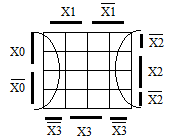То же самое можно сказать и о таблице 4-х переменных, в которой соседним кодам попарно соответствуют как нижняя и верхняя строки таблицы, так и правый и левый крайние ее столбцы (рис. 2.3.6). Поэтому таблица ФАЛ 4-х переменных как бы размещена на поверхности тора. Возможные варианты объединения в области клеток карты Вейча 4-х переменных показаны рис. 2.3.6.

Вполне очевидно, что распределение переменных по клеткам на плоском варианте карты Вейча может не совпадать с приведенным на рис. 2.3.6. Например, клетки, соответствующие переменной Х0, можно поменять местами с клетками, соответствующими переменной Х3._.Но всегда должен выполняться основной принцип заполнения карты – рядом расположенные клетки (по горизонтали и вертикали) должны соответствовать соседним кодам.

2.3.4. Приведение ФАЛ к заданному базису логических элементов. Для реализации ФАЛ произвольной сложности достаточно иметь элементы, выполняющие три основные логические операции. Это операция И (дизъюнкция), ИЛИ (конъюнкция) и НЕ (отрицание). Такая совокупность логических элементов называется функционально полной совокупностью логических элементов.

Используя принцип двойственности, согласно которому логические операции И и ИЛИ могут быть взаимно преобразованы, функционально полную систему логических элементов можно уменьшить до двух элементов. Это совокупности элементов И и НЕ или ИЛИ и НЕ. На практике, нашли применение элементы, которые совмещают две функции. Это элементы И-НЕ и ИЛИ-НЕ. Согласно вышесказанному, один такой элемент является функционально полной системой логических элементов и на его основе можно построить логическое устройство произвольной сложности.

Приведение ФАЛ к заданному базису логических элементов означает приведение функции алгебры логики к заданному типу элементов (И-НЕ или ИЛИ-НЕ), причем число входов этих элементов так же должно быть заданным.

Таким образом, проблема приведения ФАЛ к заданному базису логических элементов распадается на две самостоятельные задачи:

· приведения ФАЛ к заданному типу логических элементов (операций);

· приведение числа входов элемента к заданному числу.

2.3.5. Приведение ФАЛ к заданному типу логических элементов. Для удобства практического использования операции И-НЕ или ИЛИ-НЕ принято их изображать специальными символами:

· операция И-НЕ - операция «штрих Шеффера»,

· операция ИЛИ-НЕ - операция «стрелка Пирса».

Алгоритм приведения функции алгебры логики к заданному типу элементов базируется на использовании двух теорем алгебры логики:

· , причем дважды инвертировать можно как всё выражение, так и любую его часть;

· и - теоремы де-Моргана, являющиеся формальным представлением принципа двойственности.

Проиллюстрируем сказанное примерами.

Пример 2.3.3. Привести ФАЛ к базису элементов И-НЕ.

Решение.

В результате имеем 3 элемента 2И-НЕ и один элемент 3И-НЕ.

Пример 2.3.4. Привести ФАЛ к базису элементов ИЛИ-НЕ:

В результате имеем 3 элемента 2ИЛИ-НЕ, один элемент 3ИЛИ-НЕ и один инвертор, который так же можно выполнить на элементе ИЛИ-НЕ.

2.3.6. Приведение ФАЛ к заданному числу входов логического элемента. Здесь возможно два случая:

· число реальных входов логического элемента больше числа, требуемого ФАЛ,

· число реальных входов логического элемента меньше числа, требуемого ФАЛ.

В первом случае используются следующие формулы:

Пример 2.3.5. Привести ФАЛ к виду логических элементов с тремя входами (3И-НЕ):

Пример 2.3.6. Привести ФАЛ к виду логических элементов с тремя входами (3ИЛИ-НЕ):

Во втором случае, когда число реальных входов логического элемента меньше числа, требуемого ФАЛ, для преобразования ФАЛ можно воспользоваться теоремой , применяя ее к части выражения.

Пример 2.3.7. Преобразовать ФАЛ трехвходового элемента 3И-НЕ к базису элементов 2И-НЕ:

Пример 2.3.8. Преобразовать ФАЛ четырехвходового элемента 4И-НЕ к базису элементов 2И-НЕ:

или .

Последнее преобразование менее предпочтительно, так как при реализации приводит к большим задержкам получения результата.

Аналогично преобразуется число входов ФАЛ и элементов ИЛИ-НЕ.

Пример 2.3.9. Преобразовать ФАЛ трехвходового элемента 3ИЛИ-НЕ к базису элементов И-НЕ:

2.3.7. Вычерчивание схемы устройства по его ФАЛ. Графические эквиваленты типовых элементов ФАЛ приведены в таблице 2.3.1.

⇐ Предыдущая 1 2 3 456 7 8 9 Следующая ⇒