Сложение колебаний одного направления. Биения.

⇐ ПредыдущаяСтр 4 из 8Следующая ⇒

Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. Сложим гармонические колебания одного направления и одинаковой частоты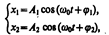

воспользовавшись методом вращающегося вектора амплитуды (см. § 140). Построим векторные диаграммы этих колебаний (рис. 203). Tax как векторы A₁ и А₂ вращаются с одинаковой угловой скоростью w₀, то разность фаз (j₂—j₁)между ними остается постоянной. Очевидно, что уравнение результирующего колебания будет (144.1) В выражении (144.1) амплитуда А и начальная фаза j соответственно задаются соотношениями (144.2) Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (j₂—j₁) складываемых колебаний. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями.

Пусть амплитуды складываемых колебаний равны А, а частоты равны w и w+Dw, причем Dw< < w. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

Складывая эти выражения и учитывая, что во втором сомножителе Dw/2< < w, найдем (144.3) Результирующее колебание (144.3) можно рассматривать как гармоническое с частотой w, амплитуда А_б, которого изменяется по следующему периодическому закону: (144.4) Частота изменения А_б в два раза больше частоты изменения косинуса (так как берется по модулю), т. е. частота биений равна разности частот складываемых колебаний: Период биений

32. Сложение взаимно перпендикулярных колебаний.

Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты w, происходящих во взаимно перпендикулярных направлениях вдоль осей х и у. Для простоты начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем

(145.1) где a — разность фаз обоих колебаний, А и В — амплитуды складываемых колебаний. Уравнение траектории результирующего колебания находится исключением из выражений (145.1) параметра t. Записывая складываемые колебания в виде

и заменяя во втором уравнении coswt на х/А и sinwt на , получим после несложных преобразований уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно: (145.2)

Если частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний.

33. Упругие волны. Скорость и длина волны. Волновое число.

Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных — в плоскостях, перпендикулярных направлению распространения волны. Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны l (рис. 220). Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебания за период, т. е. или, учитывая, что T= 1/n, где n — частота колебаний, Бегущими волнами называются волны, которые переносят в пространстве энергию. Для вывода уравнения бегущей волны — зависимости смещения колеблющейся частицы от координат и времени — рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось х совпадает с направлением распространения волны (рис. 220). Если плоская волна распространяется в противоположном направлении, то В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид

(154.2) где А = const — амплитуда волны, w — циклическая частота, j₀ — начальная фаза волны, определяемая в общем случае выбором начал отсчета х и t, [w (t—x/v)+ j₀] — фаза плоской волны. Для характеристики волн используется волновое число (154.3) Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением — дифференциальным уравнением в частных производных

или (154.9) где v — фазовая скорость, — оператор Лапласа. Решением уравнения (154.9) является уравнение любой волны. Для плоской волны, распространяющейся вдоль оси х, волновое уравнение имеет вид

34. Интерференция упругих волн.

Согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов связывают с понятием когерентности. Волны называются когерентными, если разность их фаз остается постоянной во времени. Очевидно, что когерентными могут быть лишь волны, имеющие одинаковую частоту. При наложении в пространстве двух (или нескольких) когерентных волн в разных его точках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих воли. Это явление называется интерференцией волн.

Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками S₁ и S₂ (рис. 221), колеблющимися с одинаковыми амплитудой А₀и частотой w и постоянной разностью фаз. Согласно (154.7),

где r₁ и r₂ — расстояния от источников волн до рассматриваемой точки В, k — волновое число, j₁ и j₂ — начальные фазы обеих накладывающихся сферических волн. В точках, где

(156.1) наблюдается интерференционный максимум: амплитуда результирующего колебания А=A₀/r₁ + A₀/r₂. В точках, где

(156.2) наблюдается интерференционный минимум: амплитуда результирующего колебания А=|A₀/r₁+A₀/r₂|; m=0, 1, 2, ..., называется соответственно порядком нтерференционного максимума или минимума. Условия (156.1) в (156.2) сводятся к тому, что (156.3) Выражение (156.3) представляет собой уравнение гиперболы с фокусами в точках S₁ и S₂. Следовательно, геометрическое место точек, в которых наблюдается усиление или ослабление результирующего колебания, представляет собой семейство гипербол (рис. 221), отвечающих условию (j₁ – j₂)=0. Между двумя интерференционными максимумами (на рис. 221 сплошные линии) находятся интерференционные минимумы (на рис. 221 штриховые линии).

35. Стоячая волна, узлы и пучности.

Особым случаем интерференции являются стоячее волны — это волны, образующиеся при наложении двух бегущих воли, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами, а в случае поперечных волн и одинаковой поляризацией. Получим уравнение стоячей волны: (157.2) Из уравнения стоячей волны (157.2) вытекает, что в каждой точке этой волны происходят колебания той же частоты w с амплитудой A_ст=|2А cos(2pх/l)|, зависящей от координаты х рассматриваемой точки.

В точках среды, где (157.3) амплитуда колебаний достигает максимального значения, равного 2А. В точках среды, где

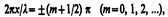(157.4) амплитуда колебаний обращается в нуль. Точки, в которых амплитуда колебаний максимальна (А_ст=2А), называются пучностями стоячей волны, а точки, в которых амплитуда колебаний равна нулю (A_ст=0), называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. что расстояния между двумя соседними пучностями и двумя соседними узлами одинаковы и равны l/2. Расстояние между соседними пучностью и узлом стоячей волны равно l/4.

36. Закон Кулона. Электрическое поле.

Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q₁ и Q₂и обратно пропорциональна квадрату расстояния r между ними: где k — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила F направлена по прямой, соединяющей взаимодействующие заряды, т. е. является центральной, и соответствует притяжению (F< 0) в случае разноименных зарядов и отталкиванию (F> 0) в случае одноименных зарядов. Эта сила называется кулоновской силой. Тогда закон Кулона запишется в окончательном виде: В данном случае говорят об электрическом поле — поле, посредством которого взаимодействуют электрические заряды. Мы будем рассматривать электрические поля, которые создаются неподвижными электрическими зарядами и называются электростатическими. Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля: Рассмотрим метод определения модуля и направления вектора напряженности Е в каждой точке электростатического поля, создаваемого системой неподвижных зарядов Q₁, Q₂, ..., Q_n. F = Q₀ E и F _i = Q₀ Е _i, где Е —напряженность результирующего поля, а Е _i — напряженность поля, создаваемого зарядом Q_i.

Формула выражаетпринцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности. Принцип суперпозиции позволяет рассчитать электростатические поля любой системы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.

37. Поток вектора напряженности. Теорема Гаусса.

Теорема Гаусса для напряжённости электрического поля в вакууме (электростатическая теорема Гаусса). Общая формулировка: Поток вектора напряжённости электрического поля через любую, произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду. В системе СИ: , где 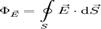— поток вектора напряженности электрического поля через замкнутую поверхность S. Q — полный заряд, содержащийся в объеме, который ограничивает поверхность S. — электрическая постоянная.

Данное выражение представляет собой теорему Гаусса в интегральной форме. В дифференциальной форме теорема Гаусса соответствует одному из уравнений Максвелла и выражается следующим образом в системе СИ: . Здесь ρ — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а — оператор набла. Применение теоремы Гаусса. Для вычисления электромагнитных полей используются следующие величины: Объёмная плотность заряда и Поверхностная плотность заряда , где dS — бесконечно малый участок поверхности. Линейная плотность заряда , где dl — длина бесконечно малого отрезка.

38. Потенциальность электростатического поля.

Электростатический потенциа́ л — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля. Единицей измерения потенциала является, таким образом, единица измерения работы, деленная на единицу измерения заряда. Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда. Напряжённость электростатического поля E и потенциал связаны соотношением:

Здесь — оператор Гамильтона, или набла, то есть в правой части равенства стоит вектор с компонентами, равными частным производным от потенциала по соответствующим координатам, взятый с противоположным знаком. Воспользовавшись этим соотношением и теоремой Гаусса для напряжённости поля , легко увидеть, что электростатический потенциал удовлетворяет уравнению Пуассона. В единицах системы СИ: где 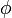— электростатический потенциал (в вольтах), — объёмная плотность заряда (в кулонах на кубический метр), а — диэлектрическая проницаемость вакуума (в фарадах на метр).

Вытекает, что отношение U/Q₀ не зависит от Q₀ и является поэтому энергетической характеристикой электростатического поля, называемой потенциалом: (84.4)

Потенциал j в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку. Из формул (84.4) и (84.2) следует, что потенциал поля, создаваемого точечным зарядом Q, равен Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, совершаемой силами поля, при перемещении единичного положительного заряда из точки 1 в точку 2. Придем к выражению для разности потенциалов:

39. Работа сил электростатического поля.

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда. Следствием независимости работы от формы траектории является следующее утверждение: Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Силовые поля, обладающие этим свойством, называют потенциальными или консервативными. Работа, совершаемая электрическим полем при перемещении точечного заряда q из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0). A12 = A10 + A02 = A10 – A20 = Wp1 – Wp2. Потенциальная энергия заряда q, помещенного в электрическое поле, пропорциональна величине этого заряда. При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении равна: Работа по перемещению пробного заряда q' из точки 1 в точку 2 не зависит от пути и выражается, как . Работа по переносу заряда q из точки 1 в точку 2 может быть записана как

40. Потенциал электростатического поля. Эквипотенциальные поверхности.

Потенциал j в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку. Потенциал поля, создаваемого точечным зарядом Q, равен (84.5) Работа, совершаемая селами электростатического поля при перемещении заряда Q₀ из точки 1 в точку 2, может быть представлена как т. е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках. Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, совершаемой силами поля, при перемещении единичного положительного заряда из точки 1 в точку 2. Если перемещать заряд Q₀ из произвольной точки за пределы поля, т. е. в бесконечность, где, по условию, потенциал равен нулю, то работа сил электростатического поля, согласно (84.6), A_¥=Q₀j, откуда . Таким образом, потенциал — физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки поля в бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля. Найдем взаимосвязь между напряженностью электростатического поля, являющейся его силовой характеристикой, и потенциалом — энергетической характеристикой поля. Работа по перемещению единичного точечного положительного заряда из одной точки поля в другую вдоль оси х при условии, что точки расположены бесконечно близко друг к другу и x₂—x₁=dx, равна E_xdx. Та же работа равна j₁—j₂=dj. Приравняв оба выражения, можем записать Из определения градиента следует, что т. е. напряженность Е поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала. Для графического изображения распределения потенциала электростатического поля, как и в случае поля тяготения, пользуютсяэквипотенциальными поверхностями — поверхностями, во всех точках которых потенциал j имеет одно и то же значение. линии напряженности в случае точечного заряда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальных поверхностей вокруг каждого заряда и каждой системы зарядов можно провести бесчисленное множество.

41. Проводники и их свойства. Явление электрической индукции.

Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действовать электростатическое поле, в результате чего они начнут перемещаться. Перемещение зарядов (ток) продолжается до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в нуль. Итак, напряженность поля во всех точках внутри проводника равна нулю: Отсутствие поля внутри проводника означает, согласно (85.2), что потенциал во всех точках внутри проводника постоянен (j = const), т. е. поверхность проводника в электростатическом поле является эквипотенциальной. При внесении проводника в электростатическое поле оно перестанет быть электростатическим; под действием сил поля по проводнику начнут двигаться заряды. Движение зарядов в проводнике можно рассматривать как перераспределение положительных и отрицательных зарядов (ранее взаимно компенсировавших друг друга во всех точках нейтрального проводника), при котором положительные заряды движутся в направлении поля, а отрицательные — в направлении, противоположном направлению поля. В результате такого перемещения на части внешней поверхности проводника, обращенной к положительным истокам электрического поля, будут скапливаться (индуцироваться) отрицательные заряды, на противоположной — положительные. Эти индуцированные заряды образуют внутри проводника собственное электрическое поле, которое направлено против внешнего поля. Электростатическая индукция — явление наведения собственного электростатического поля, при действии на тело внешнего электрического поля. Явление обусловлено перераспределением зарядов внутри проводящих тел, а также поляризацией внутренних микроструктур у непроводящих тел. Внешнее электрическое поле может значительно исказиться вблизи тела с индуцированным электрическим полем. Перераспределение электронов в хорошо проводящих металлах при действии внешнего электрического поля происходит до тех пор, пока заряды практически полностью не скомпенсируют внешнее электрическое поле внутри тела. При этом на противоположных сторонах проводящего тела появятся противоположные наведённые (индуцированные) заряды.

⇐ Предыдущая 1 2 345 6 7 8 Следующая ⇒