АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

Стр 1 из 24Следующая ⇒

КОНСПЕКТ ЛЕКЦИЙ

для студентов 4-го курса дневной формы обучения и

5-го курса заочной формы обучения

направления 6.070104 «Морской и речной транспорт»

специальности «Эксплуатация судовых энергетических установок»

Керчь, 2010

Автор: Крестлинг Н.А. к.т.н., доцент кафедры СЭУ КГМТУ;

Кулакова А.Н. ассистент кафедры

Рецензент: Конюков В.Л. к.т.н., доцент кафедры СЭУ КГМТУ;

Турега О.Н. доцент, зав. кафедрой Керченского института Таврического национального университета им. В.Вернадского

Методические указания рассмотрены и одобрены на заседании кафедры СЭУ КГМТУ,

протокол № 1 от 31.08.2010г.

Методические указания рассмотрены и рекомендованы к утверждению на заседании методической комиссии МФ КГМТУ,

протокол № 1 от 20.10.2010 г.

Методические указания утверждены на заседании Методического совета КГМТУ,

протокол №____от «___»__________201__г.

ВВЕДЕНИЕ

Автоматизация производственных процессов является ведущим направлением технического прогресса и одним из наиболее эффективных путей повышения производительности общественного труда.

Внедрение автоматизации на судах позволяет существенно повысить экономичность и моторесурс энергетических установок, сократить численность экипажа и эксплуатационные расходы, улучшить маневренные характеристики судов, облегчить труд моряков, способствует решению главной задачи — снижению себестоимости грузоперевозок в условиях безаварийного плавания.

Слова «автоматизация», «автоматика» происходят от греческого слова «автоматос», что означает «самодвижущийся» или «самодействующий».

В 50-е годы XVII столетия нидерландским механиком Гюйгенсом был разработан автомат, который должен был автоматически регулировать ход часов.

Начало промышленного использования автоматики принято считать с разработок в 1765 г. русским механиком И.И.Ползуновым поплавкого регулятора уровня воды в котле паровой машины и в 1784 г. английским механиком Джеймсом Уаттом центробежного регулятора частоты вращения вала паровой машины.

Практические разработки регуляторов способствовали к началу XIX в. развитию теории автоматического регулирования. Коренные изменения в развитии автоматики внесли фундаментальные работы Д.К.Максвелла «О регуляторах» (1866 г.), И.А.Вышнеградского «Об общей теории регуляторов» (1876 г.) и «О регуляторах прямого действия» (1877 г.), где регулятор и машина рассматривались как единая динамическая система.

Исключительно важны разработки А.М.Ляпунова, посвященные устойчивости. В работе «Общая задача об устойчивости движения» (1892 г.) он впервые дал точное определение устойчивости автоматических систем и предложил методы ее исследования.

Центральной проблемой автоматики вплоть до 40-х годов была проблема устойчивости. В ее решение особый вклад внесли английский ученый Э.Раус и немецкий – А.Гурвиц, предложившие алгебраические методы, а также американский ученый Х.Найквист и русский – А.В.Михайлов, разработавшие частотные методы исследования устойчивости.

Судовая энергетика сложилась в настоящее время в обширную научную и прикладную дисциплину, изучающую теорию автоматического регулирования и управления и построенные на ее основе судовые автоматические устройства и системы. Объектами автоматизации в ней являются различные технические средства (ТС) судна.

Установка на судах тепловых двигателей сразу же потребовала применения регуляторов частоты вращения. С развитием автоматизации общепромышленных электроприводов на судах стали применять системы управления (СУ) электроприводами вспомогательных механизмов (обслуживающих главный двигатель), шпилей, брамшпилей, грузовых лебедок, кранов и других механизмов.

Теоретической основой построения различных судовых дискретных логических управляющих устройств и комплексных систем управления (КСУ) является предложенная ирландским математиком Джорджем Булем алгебра логики и развития на ее основе теория конечных автоматов.

Комплексная автоматизация, являясь важнейшим проявлением научно-технического прогресса на морском транспорте, превращает современные суда, по существу, в человеко-машинные системы, изучение и эксплуатация которых требуют системного подхода.

Дальнейшее развитие комплексной автоматизации судов уже в настоящее время достигла такого уровня, когда можно практически осуществить безвахтенное обслуживание машинной техники. Дальнейшее развитие комплексной автоматизации связано с углублением централизации управления, применением цифровых вычислительных машин (ЦВМ), в том числе мини-ЦВМ и микро-ЦВМ, а также систем диагностики.

РАЗДЕЛ I

ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ

АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

ГЛАВА 1

ОБЩИЕ СВЕДЕНИЯ О СИСТЕМАХ

АВТОМАТИЧЕСКОГОРЕГУЛИРОВАНИЯ

Автоматизация и механизация

Судовые энергетические установки эксплуатируются в специфических условиях, в значительной степени отличающихся от береговых. Это объясняется действием качки в штормовых условиях, высокой температуры и влажного воздуха при плавании в тропических широтах, ограниченными габаритами судовых помещений и рядом других обстоятельств. Одновременно с этим к процессам управления и контроля предъявляются такие высокие требования, что человек в силу ограниченности своих физиологических возможностей не всегда в состоянии им удовлетворить, в результате чего эффективность эксплуатации установки, особенно в аварийных ситуациях, заметно снижается.

Для повышения эффективности эксплуатации энергетических установок применяют автоматизацию и механизацию производственных процессов, операций обслуживания и управления, т.е. создают устройства, заменяющие человека в сфере обслуживания управления и контроля производственного процесса.

Механизация производственного процесса заменяет мускульную силу человека силой машин. Автоматизация заменяет отдельные операции, связанные с умственной деятельностью человека, позволяя возложить на автоматические устройства функции управления и контроля. Автоматизация производственных процессов является высшей завершающей формой развития машинного производства.

Системы, в которых осуществляется автоматическое поддержание постоянного значения регулируемой величины или изменение ее по заданному закону при различных режимах работы, называются системами автоматического регулирования САР.

Автоматика — отрасль науки и техники, охватывающая совокупность технических средств и методов, обеспечивающих освобождение человека от непосредственного участия в производственном процессе в части, связанной с выполнением функций контроля и управления процессами.

Автоматическое устройство — устройство, осуществляющее управление и (или) контроль производственного процесса в зависимости от заданных условий и обеспечивающее освобождение человека от выполнения им этих функций.

Теоретической основой автоматизации является техническая кибернетика. Она рассматривает технические системы и изучает законы управления ими.

Усилители

В том случае, когда сигналы, получаемые от датчиков, недостаточны для перемещения регулирующего органа, в САР применяются усилительные устройства. Основной характеристикой усилителя является коэффициент усиления по мощности:

, (3)

где Р₁, Р₂ — соответственно входная и выходная мощности усилителя в номинальном режиме работы.

В САР применяются электрические, гидравлические, пневматические, а также комбинированные усилители.

По принципу действия электрические усилители делятся на магнитные, электронные и электромашинные.

Рис. 10. Принципиальная схема магнитного усилителя

Принцип действия магнитных усилителей основан на свойстве дросселя с железным сердечником изменять свою индуктивность при подмагничивании его постоянным током. Схема магнитного усилителя представлена на рис. 10. Простейший магнитный усилитель или дроссель насыщения состоит из железного сердечника, на котором намотаны две обмотки. В управляющую обмотку I подается постоянный ток подмагничивания, а обмотка II включена последовательно с нагрузкой в цепь переменного тока.

Полное сопротивление цепи переменного тока складывается из омического R и индуктивного nL сопротивлений. За счет изменения постоянного тока подмагничивания, протекающего через управляющую обмотку I, можно в широком диапазоне менять индуктивное сопротивление, а, следовательно, и величину переменного тока. Рассмотренная схема магнитного усилителя не пригодна для практических целей из-за наличия тока холостого хода в цепи нагрузки при отсутствии управляющего сигнала; переменного тока большого напряжения в обмотке постоянного тока.

Для устранения переменного тока большого напряжения в управляющей обмотке применяют двухдроссельные магнитные усилители (рис. 11), достоинствами которых являются высокая надежность, простота в эксплуатации, отсутствие подвижных деталей, высокий к.п.д. Недостатком их является значительная инерционность.

Рис. 11. Схема двухдроссельного магнитного усилителя

В последние годы начали получать широкое применение также усилители на полупроводниковых элементах.

Электромашинные усилители (ЭМУ) находят широкое применение в системах автоматического регулирования и управления, в следящих системах и автоматизированном электроприводе. ЭМУ имеют достаточно большой коэффициент усиления (до 10 000). В качестве простейшего ЭМУ может быть использована машина постоянного тока с независимым возбуждением, однако коэффициент усиления по мощности такого ЭМУ не превышает 20-50.

Наиболее широкое распространение получили ЭМУ с поперечным полем, представляющие собой генераторы постоянного тока с двумя ступенями усиления. Генератор приводится во вращение электродвигателем постоянного или переменного тока. Возбуждение усилителя осуществляется от обмоток управления, которые имеют независимое питание.

Принцип действия такого ЭМУ (рис. 12) заключается в следующем. Если к обмотке управления подвести небольшую мощность и создать тем самым магнитный поток, то при вращении якоря в его проводниках будет наводиться ЭДС. В связи с тем, что сопротивления обмотки якоря и короткозамкнутого витка имеют малую величину ток, протекающий в короткозамкнутом витке, будет достаточно большой силы. В результате будет создаваться магнитный поток, под действием которого в проводниках якоря наводится ЭДС и возникает ток нагрузки электромашинного усилителя. Созданная током продольная реакция якоря компенсируется действием обмотки, в результате чего первичный поток не будет зависеть от тока.

Рис. 12. Схема электромашинного усилителя

(ЭМУ) с поперечным полем

В данном усилителе первая ступень усиливает мощность P_y = I_y U_y до мощности P₂ = = I₂Е₂, а вторая ступень усиливает мощность P₂до мощности P_вых = I_нU_вых. Применяющиеся ЭМУ с поперечным полем имеют большой диапазон выходных мощностей (от сотен ватт до десятков киловатт). Конструктивно электромашинный усилитель и приводной двигатель выполняются в одном агрегате.

На рис. 13 показана схема гидравлического усилительно-силового устройства, состоящего из отсечного золотника и гидравлического сервопоршня. При перемещении золотника вверх или вниз от равновесного положения масло под рабочим давлением Р₁ поступает либо в верхнюю, либо в нижнюю полости цилиндра, а из противоположных полостей масло поршнем вытесняется на слив.

Рис. 13. Схема гидравлического усилителя с отсечным золотником:

1 – золотник; 2 – цилиндр; 3 – силовой цилиндр; 4 – сервопоршень; 5 - шток

Принцип действия струйной трубки может быть пояснен схемой, показанной на рис. 15. Жидкость либо воздух под давлением поступает из струйной трубки во входные каналы. В зависимости от отклонения струйной трубки будет изменяться давление в каналах и полостях силового цилиндра. Сервопоршень со штоком при наличии перепада давления между полостями будет перемещаться в ту либо другую сторону.

Рис. 14. Схема усилителя со струйной трубкой:

1 – струйная трубка; 2 – входные каналы;

3 – силовой цилиндр; 4 – сервопоршень; 5 - шток

Принцип работы дросселя переменного сечения рассмотрим на рис. 15. Рабочая жидкость (либо воздух) под постоянным давлением подается в усилитель через дроссели 3 и 2 на слив. В зависимости от положения заслонки в пространстве между дросселями, а также в подпоршневой полости сервомотора устанавливается давление Р. Так как поршень сервомотора находится в равновесии под действием усилия пружины сверху и давления рабочей среды снизу, то он будет перемещаться в зависимости от величины этого давления Р, определяемого в свою очередь положением заслонки.

Рис. 15. Схема усилителя с дросселем Рис. 16. Схема двухкаскадного усилителя:

переменного сечения: 1 – торцевые камеры; 2 – золотник;

1 – заслонка; 2, 3 – дроссели; 4 – серво- 3 - струйная трубка

поршень; 5 – пружина; 6 - серводвигатель

При необходимости получения больших коэффициентов усиления применяют двух- или многокаскадное усиление.

Схема двухкаскадного усилителя типа «струйная трубка — отсечный золотник» приведена на рис. 16.

Здесь струйная трубка управляет перемещением золотника, который в свою очередь управляет сервопоршнем. При перемещении струйной трубки создается повышенное давление в правой либо левой торцевой камере, в результате чего золотник переместится в левую либо правую сторону.

Электромагнитные реле

Электромагнитные реле представляют собой устройства, в которых при определенных значениях входного сигнала происходит скачкообразное изменение выходной величины. Схема электромагнитного нейтрального реле, которое одинаково срабатывает независимо от полярности тока, показана на рис. 17. При прохождении тока по катушке якорь притягивается к сердечнику и замыкает правую пару контактов. При прекращении питания пружина перебрасывает якорь, размыкает правые контакты и замыкает левые.

Рис. 17. Схема электромагнитного нейтрального реле:

1 – катушка; 2 – пружина; 3 – контакты; 4 - якорь

Схема трехпозиционного поляризованного реле показана на рис. 18. При отсутствии питания катушки якорь, расположенный между полюсами магнита, находится в среднем положении. В зависимости от полярности тока, подаваемого на катушку, якорь переместится в правое или левое положение, замыкая соответственно правую или левую пару контактов.

Рис. 18. Схема поляризованного реле: Рис. 19. Схема электро-

1 – катушка; 2 – контакты; 3 – магнит; 4 – якорь термического реле:

1 – обмотка; 2, 4 – биметаллические

пластинки; 3 - контакты

Помимо электромагнитных, широкое распространение получили также электротермические реле (рис. 19). При пропускании тока по обмотке с большим омическим сопротивлением выделяется тепло, под действием которого биметаллическая пластинка нагревается, изгибается и замыкает контакты. Для устранения влияния температуры окружающей среды правая пластинка выполнена также из биметалла.

Объекты регулирования

Несмотря на различие в устройстве и принципе действия объектов регулирования, статические и динамические свойства, а, следовательно, и поведение их в переходных процессах можно в большинстве случаев описать одним из типовых дифференциальных уравнений, которое дает математическое выражение физического закона, определяющего работу рассматриваемого объекта. Под объектом регулирования понимается машина, аппарат, устройство или система, в которых осуществляется регулирование одной или нескольких величин, называемых регулируемыми величинами.

По структуре объекты регулирования можно разделить на простейшие — одноемкостные и более сложные — многоемкостные. Работа объекта связана с преобразованием энергии или рабочего вещества. Способность объекта накапливать внутри себя рабочее вещество или энергию называется аккумулирующей способностью.

В том случае, когда объект имеет только один участок, в котором может накапливаться рабочее вещество или энергия, он называется одноемкостным объектом. Динамика одноемкостного объекта описывается дифференциальным уравнением 1-го порядка.

При наличии нескольких участков, в которых может аккумулироваться вещество или энергия, причем перетекание энергии или вещества из одного участка в другой происходит через сопротивление, объект будет называться многоемкостным. Схема двухъемкостного объекта показана на рис. 20.

Динамика многоемкостных объектов описывается дифференциальными уравнениями более высоких порядков. Для математического описания многоемкостного объекта необходимо рассматривать каждую из емкостей в отдельности с учетом взаимного влияния их друг на друга.

Рис. 20. Схема двухъемкостного объекта регулирования:

Q₁ - приток рабочего вещества; Q₂ - расход рабочего вещества;

Н₁ и Н₂ - уровни рабочего вещества; I и II - емкости

Входной координатой объекта регулирования является положение регулирующего органа, на который воздействует автоматический регулятор. Выходной координатой является регулируемая величина. Кроме того, на объект регулирования действуют внешние возмущения.

а) 6) в)

Рис. 21. Типовые возмущающие воздействия:

а - ступенчатое; 6 - импульсное; в - гармоническое

При изменении внешней нагрузки или при изменении положения регулирующего органа происходит изменение регулируемой величины на выходе объекта регулирования.

Изменение регулируемой величины во времени при изменении нагрузки или положения регулирующего органа называется переходным процессом.

Очевидно, что характеристики переходного процесса будут изменяться в зависимости от вида возмущающего воздействия. Для возможности сопоставления результатов при исследованиях на вход объекта подают так называемые типовые возмущающие воздействия, к числу которых относятся ступенчатое, импульсное и гармоническое. Схемы указанных возмущающих воздействий приведены на рис. 21. В большинстве случаев исследование переходных процессов производится при резком скачкообразном изменении положения регулирующего органа на небольшую величину, т.е. при ступенчатом возмущении. Такой характер возмущения является одним из наиболее сильных и позволяет по характеру переходного процесса, т.е. по изменению регулируемой величины во времени от одного установившегося режима до другого, определить статические и динамические свойства объекта регулирования.

Автоматические регуляторы

Автоматический регулятор формирует закон регулирования и обеспечивает заданные динамические свойства САР. Автоматические регуляторы разделяются на регуляторы прямого и непрямого действия. В регуляторах непрямого действия перемещение регулирующего органа осуществляется за счет энергии постороннего источника, в зависимости от вида которой различают электрические, пневматические, гидравлические и комбинированные регуляторы.

В общем случае регулятор можно отнести к колебательному звену, динамика которого описывается уравнением 2-го порядка [см. уравнение (50)]. Однако в связи с тем, что постоянные времени Т₁и Т₂в уравнении (50) обычно во много раз меньше постоянной времени объекта Т₀, в практических расчетах ими часто пренебрегают и считают регулятор идеальным звеном [см. уравнение (29)].

В зависимости от характеристики действия регуляторы делятся:

на статические или пропорциональные (П-регуляторы), в которых регулирующее воздействие пропорционально отклонению регулируемой величины; уравнение динамики идеального статического регулятора имеет вид:

; (29)

на астатические или интегральные (И-регуляторы), у которых регулирующее воздействие пропорционально интегралу отклонения регулируемой величины; уравнение динамики идеального астатического регулятора имеет вид:

; (30)

на изодромные или пропорционально-интегральные (ПИ-регуляторы), у которых регулирующее воздействие пропорционально отклонению и интегралу отклонения регулируемой величины; уравнение динамики идеального изодромного регулятора имеет вид:

; (31)

на регуляторы с воздействием по производной (или ПД-регуляторы), у которых регулирующее воздействие пропорционально отклонению и производной отклонения регулируемой величины. Применяются также регуляторы, у которых регулирующее воздействие пропорционально отклонению, производной и интегралу отклонения регулируемой величины — изодромные с воздействием по производной (ПИД-регуляторы); уравнение динамики ПИД-регулятора имеет вид:

. (32)

ГЛАВА 2

ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И

ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ

Передаточная функция

Помимо дифференциального уравнения, динамические свойства звена могут быть описаны также при помощи передаточной функции, которая представляет собой отношение операторного полинома воздействия ксобственному операторному полиному, т.е. в общем виде передаточная функция звена определяется выражением

, (39)

а передаточная функция объекта, динамика которого описывается уравнением (13), выражением

. (40)

Частотная характеристика

В ряде случаев системы автоматического регулирования и входящие в состав их звенья работают под воздействием периодических и, в частности, гармонических возмущений. В связи с этим возникает необходимость исследовать работу систем также в режиме вынужденных колебаний с помощью, так называемого частотного метода. Отличительной особенностью частотного метода является также возможность применения его для экспериментального исследования динамических свойств реальных систем, аналитическое исследование которых невозможно.

Если на вход линейного звена подать гармоническое возмущение с амплитудой A₁ и частотой w, при этом , то по прошествии некоторого времени выходная координата также будет изменяться по гармоническому закону с той же частотой w, но с другой амплитудой А₂ и сдвигом колебаний по фазе j. Графически это показано на рис. 25.

Частотной характеристикой звена или амплитудно-фазовой частотной характеристикой называется зависимость амплитуды и фазы вынужденных гармонических колебаний от амплитуды и частоты входного возмущения.

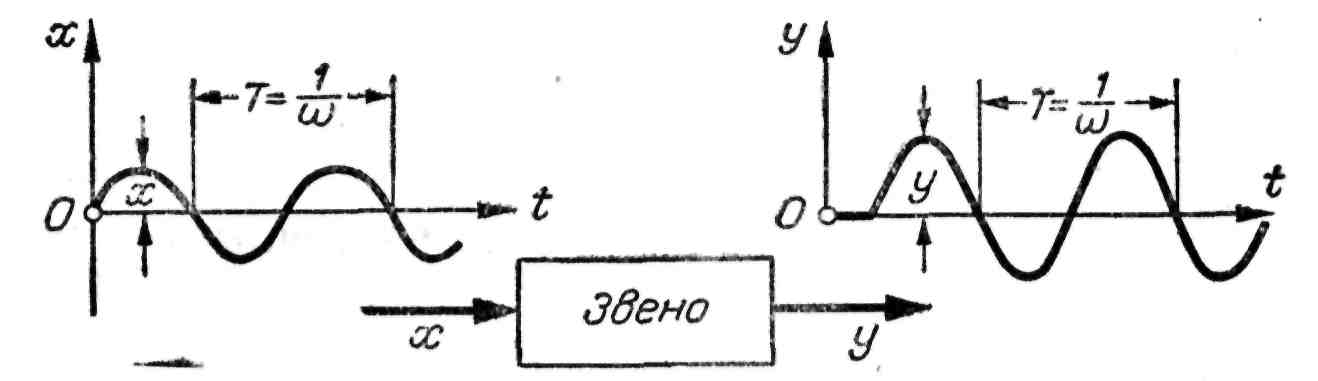
Рис. 25. Вынужденные колебания САР

Для получения частотной функции, называемой также комплексной передаточной функцией, необходимо в выражение передаточной функции вместо р подставить iw, где , а w — круговая частота, т.е.

. (41)

Рис. 26. Амплитудно-фазовая характеристика

Последнее выражение в общем виде можно представить в прямоугольной системе координат:

, (42)

либо в полярной системе в виде показательной функции:

(43)

где — модуль, определяющий амплитуду колебаний;

— фаза.

Если изобразить частотную функцию (43) в виде вектора в комплексной плоскости , то при изменении частоты w от 0 до ∞ конец вектора опишет кривую, называемую амплитудно-фазовой характеристикой. Пример такой кривой приведен на рис. 26. Амплитудно-фазовые характеристики широко используются при исследовании динамических свойств систем.

Типовые динамические звенья

Несмотря на то, что звенья, входящие в состав различных САР, отличаются во многих случаях друг от друга как по конструктивному выполнению, так и по функциональному назначению, представляется возможным свести их к сравнительно небольшой группе звеньев, отличающихся одинаковыми динамическими свойствами. При такой классификации по динамическим свойствам звенья, переходные процессы в которых описываются одинаковыми уравнениями, относят к одному типу динамического эвена.

В теории автоматического регулирования принято различать следующие основные динамические звенья: пропорциональное или безынерционное, апериодическое или инерционное, колебательное, дифференцирующее, интегрирующее, с чистым запаздыванием.

Динамические свойства пропорционального или безынерционного звена описываются уравнением вида:

, (44)

а переходный процесс имеет вид, изображенный на рис. 27.

Рис. 27. Переходный процесс безынерционного звена

Передаточная и частотная функции этого звена описываются следующими выражениями:

; (45)

. (46)

Динамика апериодического звена описывается уравнением

. (47)

При ступенчатом возмущении и нулевых начальных условиях переходная функция имеет вид (см. рис. 22):

. (48)

Передаточная и частотная функции этого звена имеют следующие выражения:

;

(49)

Амплитудно-фазовая характеристика этого звена представлена на рис. 28.

Рис. 28. Амплитудно-фазовая характеристика

апериодического звена 1-го порядка

Динамика колебательного звена описывается уравнением

. (50)

При ступенчатом возмущении и нулевых начальных условиях переходная функция имеет вид (рис. 29):

, (51)

где — постоянная времени огибающей экспоненты;

Передаточная и частотная функции колебательного звена будут иметь выражения:

; (52)

. (53)

Рис. 29. График переходного процесса колебательного звена

Амплитудно-фазовая характеристика колебательного звена представлена на рис. 26.

В том случае, если в уравнении будет иметь место неравенство , то звено превращается в апериодическое 2-го порядка с переходной функцией

, (54)

где

;

Переходный процесс в этом случае будет иметь вид, представленный на рис. 30.

Рис. 30. График переходного процесса

апериодического звена 2-го порядка

Идеальным дифференцирующим называется звено, динамика которого описывается уравнением вида:

. (55)

График переходной функции этого звена показан на рис. 31 и представляет собой мгновенный импульс, который возникает только в момент подачи ступенчатого входного возмущения. Передаточная и частотная функции идеального дифференцирующего звена:

; . (56)

Рис. 31. Переходный процесс идеального

дифференцирующего звена

Большинство реальных систем обладают определенной инерционностью. Динамика инерционного дифференцирующего звена может быть описана уравнением вида:

. (57)

Рис. 32. Переходный процесс идеального интегрирующего звена

Динамика идеального интегрирующего звена описывается уравнением вида

(58)

или

, (59)

а в операторной форме

. (60)

Из уравнения (58) следует, что если на вход интегрирующего звена подать ступенчатое возмущение, то выходная величина будет со временем беспрерывно увеличиваться.

Графики переходного процесса такого звена показаны на рис. 32. Передаточная и частотная функции определяются по уравнениям:

(61)

Уравнение динамики реального интегрирующего звена будет:

. (62)

Дифференцируя обе части уравнения, можно получить другое выражение:

. (63)

В ряде случаев изменение выходной величины начинается не одновременно с изменением входной, а спустя некоторый промежуток времени, называемый запаздыванием.

Различают звенья с чистым или транспортным запаздыванием, примером которого может служить ленточный питатель (рис. 33). Если входной координатой считать положение шибера на питающем бункере 1 (х), а выходной координатой — количество материала, поступающего в бункер (Q), то переходная характеристика этого звена может быть описана уравнением

, (64)

где t — время;

— время чистого или транспортного запаздывания.

Рис. 33. Схема звена с чистым запаздыванием:

1, 3 – бункера; 2 - шибер

В общем случае любое звено с запаздыванием можно рассматривать состоящим из обыкновенного звена без запаздывания и идеального звена с чистым запаздыванием. Передаточная функция звена с запаздыванием в общем случае будет иметь выражение

, (65)

где W₀(p) — передаточная функция звена без запаздывания.

Рис. 34. Переходные процессы:

а – идеальное звено с чистым запаздыванием;

б – инерционное звено с чистым запаздыванием

Переходные процессы для идеального звена с запаздыванием и для инерционного звена при наличии чистого запаздывания приведены на рис. 34.

ГЛАВА 3

Определение устойчивости

Основным назначением САР является поддержание регулируемой величины на заданном уровне при наличии воздействия на систему внешних возмущений. Поэтому систему автоматического регулирования называют устойчивой, если, будучи выведенной из состояния равновесия и предоставленной самой себе, она с течением времени будет стремиться вернуться к равновесному состоянию.

Устойчивость системы определяется характером свободного движения, которое, как известно, описывается однородным дифференциальным уравнением (без правой части). Поэтому форма правой части уравнения, описывающего динамику системы, не оказывает влияния на устойчивость.

В общем случае свободное движение системы можно описать однородным дифференциальным уравнением вида:

, (72)

где у — регулируемая величина;

а₀, а₁... а_п — постоянные коэффициенты, определяемые параметрами системы.

Согласно определению система будет устойчивой, если

(73)

Решение уравнения (72) можно представить в следующем виде:

, (74)

где С_i — постоянные интегрирования, определяемые из начальных условий,

p_i — корни характеристического уравнения (75), соответствующего дифференциальному уравнению (72):

. (75)

Условие (73) может быть выполнено в том случае, если все составляющие решения (74) с течением времени будут стремиться к нулю. Так как все коэффициенты С_i — величины постоянные, то характер каждой составляющей зависит только от p_i.

Если p_i будет положительной вещественной величиной, то будет с течением времени увеличиваться до бесконечности. Если p_i будет отрицательной вещественной величиной, то будет с течением времени стремиться к нулю. В том случае, если — комплексная величина, то

—

12 3 4 5 6 7 8 9 10 Следующая ⇒