Выбор типа и настройки регулятора

⇐ ПредыдущаяСтр 4 из 24Следующая ⇒

Как уже указывалось ранее, САР является динамической системой, статические и динамические характеристики которой (зависимость выходной величины от входной в статике и динамике) определяются характеристиками объекта регулирования и регулятора, а также типом возмущений.

Поэтому при выборе типа регулятора должны учитываться основные характеристики объекта, а также требования, предъявляемые к техническим показателям регулирования (продолжительность переходного процесса, колебательность, статическая и динамическая ошибки).

Так, объекты с большим коэффициентом самовыравнивания могут оборудоваться любым типом регулятора, и если нет особых требований к показателям переходного процесса, то для автоматического регулирования можно использовать простейшие П-регуляторы и И-регуляторы. При наличии больших запаздываний и в то же время медленно изменяющихся возмущениях обычно применяют ПИ-регуляторы, а при резких и частых возмущениях — ПИД-регуляторы. Необходимо отметить, что правильный выбор типа регулятора является очень важной и в то же время достаточно сложной задачей. При настройке регулятора преследуются две цели: обеспечение устойчивой работы САР, под которой понимается способность системы возвращаться к равновесному состоянию после получения возмущений, а также получение требуемого техническими условиями качества регулирования. Параметрами настройки регуляторов являются коэффициенты усиления и, в зависимости от закона регулирования, различные постоянные времени.

Для сложных систем автоматического регулирования до настройки в натурных условиях часто выполняют исследования и настройку модели системы, которая набирается на моделирующих электронных установках.

Вопросы для самоконтроля:

1. Какие системы называются системами автоматического регулирования (САР)?

2. Назвать элементы систем автоматического регулирования.

3. Назначение потенциометрического и индуктивного датчиков.

4. Принцип действия пьезоэлектрического датчика и сельсина.

5. Назначение и устройство магнитных усилителей.

6. Объект и статический регулятор (П-регулятор). Динамика САР.

7. Объект и изодромный регулятор (ПИ-регулятор).

Литература [4, 5, 6].

ГЛАВА 2

ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И

ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ

Передаточная функция

Помимо дифференциального уравнения, динамические свойства звена могут быть описаны также при помощи передаточной функции, которая представляет собой отношение операторного полинома воздействия ксобственному операторному полиному, т.е. в общем виде передаточная функция звена определяется выражением

, (39)

а передаточная функция объекта, динамика которого описывается уравнением (13), выражением

. (40)

Частотная характеристика

В ряде случаев системы автоматического регулирования и входящие в состав их звенья работают под воздействием периодических и, в частности, гармонических возмущений. В связи с этим возникает необходимость исследовать работу систем также в режиме вынужденных колебаний с помощью, так называемого частотного метода. Отличительной особенностью частотного метода является также возможность применения его для экспериментального исследования динамических свойств реальных систем, аналитическое исследование которых невозможно.

Если на вход линейного звена подать гармоническое возмущение с амплитудой A₁ и частотой w, при этом , то по прошествии некоторого времени выходная координата также будет изменяться по гармоническому закону с той же частотой w, но с другой амплитудой А₂ и сдвигом колебаний по фазе j. Графически это показано на рис. 25.

Частотной характеристикой звена или амплитудно-фазовой частотной характеристикой называется зависимость амплитуды и фазы вынужденных гармонических колебаний от амплитуды и частоты входного возмущения.

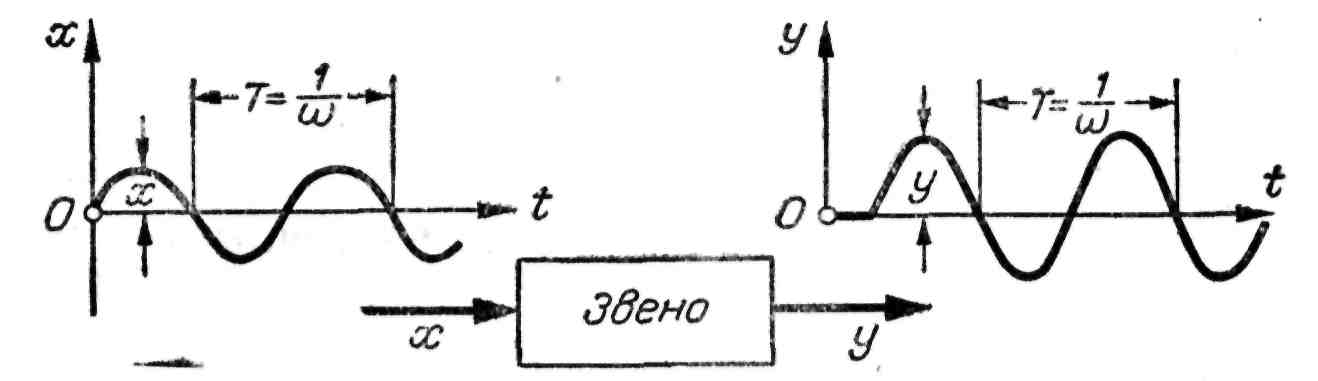
Рис. 25. Вынужденные колебания САР

Для получения частотной функции, называемой также комплексной передаточной функцией, необходимо в выражение передаточной функции вместо р подставить iw, где , а w — круговая частота, т.е.

. (41)

Рис. 26. Амплитудно-фазовая характеристика

Последнее выражение в общем виде можно представить в прямоугольной системе координат:

, (42)

либо в полярной системе в виде показательной функции:

(43)

где — модуль, определяющий амплитуду колебаний;

— фаза.

Если изобразить частотную функцию (43) в виде вектора в комплексной плоскости , то при изменении частоты w от 0 до ∞ конец вектора опишет кривую, называемую амплитудно-фазовой характеристикой. Пример такой кривой приведен на рис. 26. Амплитудно-фазовые характеристики широко используются при исследовании динамических свойств систем.

Типовые динамические звенья

Несмотря на то, что звенья, входящие в состав различных САР, отличаются во многих случаях друг от друга как по конструктивному выполнению, так и по функциональному назначению, представляется возможным свести их к сравнительно небольшой группе звеньев, отличающихся одинаковыми динамическими свойствами. При такой классификации по динамическим свойствам звенья, переходные процессы в которых описываются одинаковыми уравнениями, относят к одному типу динамического эвена.

В теории автоматического регулирования принято различать следующие основные динамические звенья: пропорциональное или безынерционное, апериодическое или инерционное, колебательное, дифференцирующее, интегрирующее, с чистым запаздыванием.

Динамические свойства пропорционального или безынерционного звена описываются уравнением вида:

, (44)

а переходный процесс имеет вид, изображенный на рис. 27.

Рис. 27. Переходный процесс безынерционного звена

Передаточная и частотная функции этого звена описываются следующими выражениями:

; (45)

. (46)

Динамика апериодического звена описывается уравнением

. (47)

При ступенчатом возмущении и нулевых начальных условиях переходная функция имеет вид (см. рис. 22):

. (48)

Передаточная и частотная функции этого звена имеют следующие выражения:

;

(49)

Амплитудно-фазовая характеристика этого звена представлена на рис. 28.

Рис. 28. Амплитудно-фазовая характеристика

апериодического звена 1-го порядка

Динамика колебательного звена описывается уравнением

. (50)

При ступенчатом возмущении и нулевых начальных условиях переходная функция имеет вид (рис. 29):

, (51)

где — постоянная времени огибающей экспоненты;

Передаточная и частотная функции колебательного звена будут иметь выражения:

; (52)

. (53)

Рис. 29. График переходного процесса колебательного звена

Амплитудно-фазовая характеристика колебательного звена представлена на рис. 26.

В том случае, если в уравнении будет иметь место неравенство , то звено превращается в апериодическое 2-го порядка с переходной функцией

, (54)

где

;

Переходный процесс в этом случае будет иметь вид, представленный на рис. 30.

Рис. 30. График переходного процесса

апериодического звена 2-го порядка

Идеальным дифференцирующим называется звено, динамика которого описывается уравнением вида:

. (55)

График переходной функции этого звена показан на рис. 31 и представляет собой мгновенный импульс, который возникает только в момент подачи ступенчатого входного возмущения. Передаточная и частотная функции идеального дифференцирующего звена:

; . (56)

Рис. 31. Переходный процесс идеального

дифференцирующего звена

Большинство реальных систем обладают определенной инерционностью. Динамика инерционного дифференцирующего звена может быть описана уравнением вида:

. (57)

Рис. 32. Переходный процесс идеального интегрирующего звена

Динамика идеального интегрирующего звена описывается уравнением вида

(58)

или

, (59)

а в операторной форме

. (60)

Из уравнения (58) следует, что если на вход интегрирующего звена подать ступенчатое возмущение, то выходная величина будет со временем беспрерывно увеличиваться.

Графики переходного процесса такого звена показаны на рис. 32. Передаточная и частотная функции определяются по уравнениям:

(61)

Уравнение динамики реального интегрирующего звена будет:

. (62)

Дифференцируя обе части уравнения, можно получить другое выражение:

. (63)

В ряде случаев изменение выходной величины начинается не одновременно с изменением входной, а спустя некоторый промежуток времени, называемый запаздыванием.

Различают звенья с чистым или транспортным запаздыванием, примером которого может служить ленточный питатель (рис. 33). Если входной координатой считать положение шибера на питающем бункере 1 (х), а выходной координатой — количество материала, поступающего в бункер (Q), то переходная характеристика этого звена может быть описана уравнением

, (64)

где t — время;

— время чистого или транспортного запаздывания.

Рис. 33. Схема звена с чистым запаздыванием:

1, 3 – бункера; 2 - шибер

В общем случае любое звено с запаздыванием можно рассматривать состоящим из обыкновенного звена без запаздывания и идеального звена с чистым запаздыванием. Передаточная функция звена с запаздыванием в общем случае будет иметь выражение

, (65)

где W₀(p) — передаточная функция звена без запаздывания.

Рис. 34. Переходные процессы:

а – идеальное звено с чистым запаздыванием;

б – инерционное звено с чистым запаздыванием

Переходные процессы для идеального звена с запаздыванием и для инерционного звена при наличии чистого запаздывания приведены на рис. 34.

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒