Силы: сила тяжести Мд, реакции опоры N и сила

трения покоя?. Уравнение поступательного
движения в проекциях на оси ОХ и OY имеет вид:

Подставляя (3.16) в (3.15) и исключая f с
помощью (3.14), окончательно получим

6. Закон сохранения момента
импульса

В заключение отметим, что если тело
вращается вокруг закрепленной в пространстве
оси, и на него не действуют внешние силы, то из

Уравнение вращательного движения

относительно оси OZq (направленной от нас)
выглядит следующим образом:

Цилиндра относительно оси OZq и R (радиус

цилиндра) - плечо силы f. Так как силы тяжести
и реакции опоры проходят через ось OZq, их

подразумевающейся нами неизменности самого
тела при вращении, т.е. неизменности его
момента инерции. Если же взаимное
расположение частей тела (а тем самым и момент
инерции) меняется, то при свободном вращении

Лекция 4. РАБОТА И ЭНЕРГИЯ

Работа постоянной и переменной силы; теорема о кинетической энергии;
потенциальные силы; потенциальная энергия; закон сохранения энергии.

1. Работа постоянной и переменной
силы

Из школьного курса физики мы знаем, что при
движении частицы по прямолинейной траектории
постоянная по величине и направлению сила

f совершает над частицей работу

где f — модуль силы, As — отрезок
прямолинейного пути и а — угол между
направлениями силы и перемещения. Выражение
(4.1) можно записать в виде

Интеграл в правой части (4.3) называется
криволинейным интегралом 1-го рода. Из (4.3)
следует, что при движении частицы из точки 2 в
точку 1 по той же самой траектории работа силы

Вспомним теперь, что ds = |dr|, где dr —
вектор бесконечно малого перемещения. Тогда

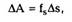
где f_s — проекция силы на перемещение. Из
определения работы видно, что последняя может
быть как положительной, когда f_s> 0, так и
отрицательной, когда f_s< 0, и равной нулю, когда
сила перпендикулярна перемещению.

Спрашивается, как найти работу силы f,
которая в разных точках траектории движения
различна по величине и направлению (говорят,
что частица движется в неоднородном силовом

поле f(x, y, z))_r а сама траектория криволинейна
(см. рис.4.1).

Поступают следующим образом. Всю
траекторию от начальной точки 1 до конечной 2
разбивают на бесконечно малые участки ds,
которые в силу своей бесконечной малости можно
считать прямолинейными. Опять же в силу того,
что путь ds бесконечно малый, можно считать, что

сила f остается постоянной как по величине, так и
по направлению на этом участке пути ds. Тогда,

Работа же силы f на конечном участке траектории от начальной точки 1 до конечной 2

согласно (4.1), элементарная работа силы f на
пути ds

Последний интеграл называется

Криволинейным интегралом 2-го рода,

вычисление которого, как правило, проще, чем
вычисление криволинейного интеграла 1-го рода.

Мощностью силы f называется работа силы в
единицу времени.

Так как за бесконечно малое время dt сила

совершает работу dA = f_sds = fdr, то мощность

Теорема о кинетической энергии

ускорение частицы, получим

Пусть частица массой m движется из точки 1 в
точку 2 по криволинейной траектории под

Сокращая на dt и преобразуя левую часть

Интегрируя теперь (4.8) от начальной точки 1
до конечной 2, получим окончательно:

где v_{ — скорость тела в начале и v₂ — в конце.
Выражение

называется кинетической энергией

материальной точки, а (4.9) — теоремой о
кинетической энергии: приращение

в точку 2 вдоль кривой а, а затем из точки 2 назад
в точку 1 вдоль кривой Ь. Общая работа, которая
производится при этом консервативной силой

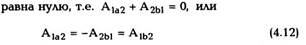
т.е. работа не зависит от вида кривой,
соединяющей начальную и конечную точки 1 и 2.
Этот факт свидетельствует о том, что работа
консервативной силы является величиной,
имеющей глубокое физическое содержание.

Потенциальная энергия

Определим теперь важную характеристику
потенциального силового поля. Примем для этого
какую-либо точку в пространстве, которую

Потенциальные силы

Среди всех сил в природе существует целый
класс сил (не изменяющихся со временем),
обладающих следующим замечательным

свойством: если частица движется по замкнутому
пути, так что в результате движения она
возвращается в исходную точку, то работа,
совершаемая при этом силой, будет равна нулю.
Силы, обладающие таким свойством, называются
консервативными, или потенциальными. Если

сила f консервативна, то математически условие
потенциальности можно записать в следующем
виде:

где кружок означает, что интеграл вычисляется по
замкнутому пути L.

Кстати, интеграл типа (4.11) для произвольного

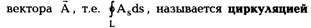
вектора А по замкнутому контуру L. Таким

образом, сила f потенциальна, если ее
циркуляция по любому замкнутому контуру равна
нулю.

Условие потенциальности можно

сформулировать другим способом: работа
консервативной силы при переносе частицы из
какой-то начальной точки 1 в конечную 2 не
зависит от вида пути, по которому происходит
перенос, а определяется только положением
начальной и конечной точек.

Действительно, рассмотрим две точки 1 и 2 и
соединим их двумя кривыми а и b (рис.4.2).
Предположим, что частица переводится из точки 1

обозначим через О, за начало отсчета и будем
рассматривать работу консервативной силы при
переходе частицы из какой-либо произвольной
точки P(x, y, z) в точку О (рис.4.3). Величина этой
работы называется потенциальной энергией
частицы.находящейся в точке Р, в потенциальном
силовом поле.

Она является функцией координат х, у, z
точки Р в неподвижной системе отсчета, т.е.

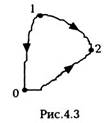
Работа консервативной силы? (рис.4.3) при
переходе частицы из точки 1 в точку 2 (работа не
зависит от пути! ):

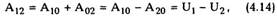
т.е. работа консервативной силы равна убыли
потенциальной энергии.

Это значит, что проекция силы на некоторое
направление s равна производной от U по
направлению s. Выражение (4.15) можно записать
в виде

откуда следует ( поскольку dU является полным
дифференциалом), что

лежит ниже нулевого уровня, z< 0 и
потенциальная энергия отрицательна.

Пусть теперь имеются две частицы Мит,
которые притягиваются друг к другу силой

частицы m в точке Р, расположенной на
расстоянии г от М. Нулевой уровень выбираем на
бесконечном расстоянии от частицы М. Тогда

Тогда (4.17) принимают вид:

Такие фундаментальные силы в природе, как
гравитационная и электрическая, являются силами
консервативными, для которых можно ввести
соответствующие потенциальные энергии. Так,
например, если частица m находится вблизи
поверхности Земли, то на нее действует
гравитационная сила тяжести mg, являющаяся
консервативной.

Выбираем точку О (начало отсчета
потенциальной энергии) на какой-то высоте над
поверхностью Земли и находим потенциальную

Такое же выражение мы получим, если
зафиксируем частицу m и будем перемещать на
бесконечность частицу М, поэтому потенциальная
энергия (4.21) называется потенциальной
энергией гравитационного взаимодействия двух
частиц m и М. Она обращается в нуль, когда
частицы удалены друг от друга на бесконечно
большое расстояние. Эта же формула остается
справедливой, если частица m находится вне
однородного шара массой М (например, планеты).
В этом случае г — расстояние от частицы m до
центра шара.

Сила упругости пружины f = kx тоже
является консервативной. Нетрудно показать, что
потенциальная энергия деформированной
пружины

энергию частицы в произвольной точке P(z)
(рис.4.5) как работу постоянной силы mg,
направленной вертикально вниз, при

перемещении частицы из точки Р в точку О по
любому пути. Выбираем путь РАО. Тогда

так как А_РА = mgz и А_АО = 0 (здесь сила
перпендикулярна перемещению). Если точка Р

Причем нулевому уровню, как видно из (4.22),
соответствует состояние, когда пружина
недеформирована, т.е. когда х = 0.

Закон сохранения энергии

Вернемся теперь снова к теореме о
кинетической энергии (4.9). Пусть среди сил \,
действующих на частицу т, часть сил является

Следует помнить при решении конкретных
задач, что типичными неконсервативными силами
являются силы трения и силы сопротивления. Из
(4.23) следует закон сохранения энергии для
материальной точки: полная энергия частицы не

изменяется, __ если__ на__ нее__ действуют__ только

консервативные силы.

Рассмотрим теперь систему из п
взаимодействующих между собой материальных
точек. Полная механическая энергия системы Е
складывается теперь из кинетической энергии
системы

Потенциальная энергия взаимодействия частиц системы U_B₃ определяется следующим образом:

потенциальной энергии взаимодействия U_R₃частиц системы, которая определяется их
консервативными силами взаимодействия, и
потенциальных энергий частиц в поле всех

находится их энергия взаимодействия U^ подобно

Итак, полная механическая энергия системы

тому, как это делалось при выводе формулы (4.21)
для энергии взаимодействия двух масс,
притягивающихся согласно закону всемирного
тяготения. После этого

неконсервативных, как внутренних, так и
внешних сил. Если таких сил нет, полная энергия
Е (4.27) системы не изменяется со временем
(закон сохранения энергии для системы).

Используем теперь полученные соотношения
(4.25) — (4.27) для абсолютно твердого тела,
рассматривая его как совокупность жестко
связанных материальных точек. Полную энергию
тела на основании (4.27) можно записать в

следующем виде (полагая U_B₃ частиц тела равной
нулю):

Следует отметить, что при плоском движении
и скорость v_t, и v_iBp находятся в плоскости XOY

Предыдущая 1 2 345 6 7 8 9 Следующая