Перепишем это равенство в момент времени

Явление резкого возрастания амплитуд *j
вынужденных колебаний при приближении
При слабом затухании амплитуда колебаний
Лекция 7. ВОЛНЫ
Плоская монохроматическая волна; волновое уравнение; волновой пакет;
дисперсия.
 1. Плоская монохроматическая волна
1. Плоская монохроматическая волна
Когда мы говорим о волнах, то представляем
себе прежде всего волны на поверхности воды,
или волны, бегущие в упругом шнуре при
периодическом сотрясении его конца. Какова бы,
однако, ни была природа волн, распространение
их следует одинаковым законам.
Волны бывают поперечные и продольные. В
поперечной волне частицы среды, в которой
распространяется волна, колеблются в
направлении, перпендикулярном направлению
распространения волны (волны на поверхности
воды, или волны, бегущие в упругом шнуре). В
продольной же волне направление колебаний
совпадает с направлением распространения волны
(звуковые волны в газе).
Рассмотрим простейший вид волн — плоские
монохроматические или гармонические волны -
и выберем направление распространения волн за
ось ОХ системы координат. Такие волны
представляются формулой
отклонение частицы от положения равновесия в
упругой волне, какая-нибудь составляющая
напряженности электрического или магнитного
поля в электромагнитной волне и т.д. Постоянная

Поверхность, во всех точках которой фаза
имеет одно и то же значение называется
волновой поверхностью. Очевидно, что в
рассматриваемом случае, когда фаза линейно
зависит от координаты х, такой поверхностью в
фиксированный момент времени t = t0 будет
плоскость х = const, нормаль к которой совпадает
с направлением распространения волны (осью
ОХ). Поэтому и говорят, что выражение (7.1)
описывает плоскую волну.
Постоянная v, входящая в фазу, имеет
следующий смысл. Выберем какое-то
определенное значение фазы, и посмотрим, при
каких условиях оно будет сохранять одну и ту же
величину при изменении х и t. Очевидно, что для
постоянства фазы необходимо и достаточно,

Отсюда видно, что v есть скорость
перемещения плоскости равной фазы (волновой
поверхности), или фазовая скорость волны.
Так как t и х входят в аргумент периодической
функции, то волна должна обнаруживать
периодичность как во времени, так и в
пространстве. Вследствие периодичности во
времени должен существовать постоянный
промежуток времени Т (период колебаний),
удовлетворяющий условию
соотношение, связывающее фазовую скорость v с
длиной волны к и периодом колебаний Т.
Пусть теперь плоская волна распространяется
в произвольном направлении, образующем с
где
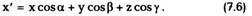
Уравнение волновой поверхности в этом
случае будет
Введем теперь вектор к, по направлению
совпадающий с положительной нормалью к
волновой поверхности, а по абсолютной величине
равный


так называемый оператор Лапласа. Тогда волновое
уравнение можно записать в более компактной
форме:
Компоненты этого вектора, который мы будем
называть волновым вектором, таковы
где г — радиус-вектор, проведенный из начала
координат в произвольную точку волновой
поверхности. При помощи (7.9) формула плоской
волны приводится к следующему компактному
виду:

2. Волновое уравнение
Рассмотренная в предыдущем разделе формула
плоской волны является частным решением
некоторого дифференциального уравнения,
называемого волновым уравнением.
Легко убедиться в том, что формула плоской
волны (7.10) удовлетворяет уравнению

Действительно, дифференцируя (7.10) дважды
по координатам и по времени, находим
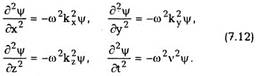
Подставляя (7.12) в (7.11), получаем после
сокращений
Это уравнение называется еще уравнением
Д'Аламбера.
Волновое уравнение является линейным
однородным дифференциальным уравнением в
частных производных. Как всякое однородное
линейное уравнение оно обладает следующим
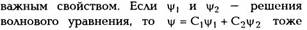
является его решением. В этом заключается
математическое обоснование известного
принципа суперпозиции волновых движений,
который позволяет при помощи наложения
плоских волн строить любые волновые поля.
3. Волновой пакет
Рассмотренные в предыдущем разделе плоские
волны в природе никогда не осуществляются. В
самом деле, по условию, эти волны представляют
строго периодический процесс, а для этого они
должны иметь бесконечное протяжение в
пространстве и во времени. Реальные же волны
всегда ограничены в пространстве и испускаются
в течение ограниченных промежутков времени, а
потому и не являются строго гармоническими.
Поэтому мы можем их рассматривать как
результат суперпозиции строго гармонических
плоских волн, которые в одной части
пространства усиливают друг друга, а в остальном
пространстве друг друга погашают (это явление
называется интерференцией волн). Такие
сложные волны имеют некоторые важные
особенности, которые мы выясним на примере
суперпозиции двух плоских гармонических волн.
Положим, что обе эти волны с одинаковой
амплитудой А распространяются вдоль оси ОХ и


Это важное соотношение, связывающее
частоту со с волновым числом к, характерно для
природы волны и называется дисперсионным
уравнением.
Вместо того, чтобы писать в левой части (7.11)
сумму вторых частных производных по
координатам, мы можем представить ее так:

Дисперсия
Обратимся теперь к рассмотрению обеих
скоростей волн — фазовой и групповой — и
сравним их между собой. Из определения
фазовой скорости (7.19) следует, что
скоростью волн. Для того, чтобы ее отыскать,
напишем условие постоянства фазы волны:

Тогда групповая скорость (см. (7.20))

откуда фазовая скорость
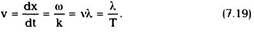
Найдем теперь отдельно скорость
перемещения определенной амплитуды волны
Очевидно, что эта скорость совпадает со
скоростью перемещения группы в целом; она
называется поэтому групповой скоростью. Для
отыскания ее пишем, по аналогии с предыдущим,
условие постоянства амплитуды:

Если фазовая скорость v, образующих пакет
гармонических волн, не зависит от к (или X), то
говорят, что среда, в которой распространяется
волна, не обладает дисперсией. В этом случае
| и будем называть групповой скоростью:
|
Мы видим, таким образом, что обе эти
скорости: фазовая и групповая, выражаются
различными формулами. Чтобы разобраться в
соотношении между ними, нужно рассмотреть
условия распространения волн в различных
средах.
Можно показать, что путем суперпозиции
плоских волн можно осуществить волновой
процесс, в котором амплитуда отлична от нуля
только в небольшой части пространства Δ х, а в
остальном пространстве равна нулю. Для этого
нужно, чтобы волновые числа плоских волн
лежали в некотором интервале Δ к, причем
Соотношение (7.21), как мы узнаем позже,
приводит к знаменитым соотношениям
неопределенностей Гейзенберга в квантовой
механике.
При наличии же дисперсии групповая скорость
не совпадает с фазовой, а именно, в зависимости
от знака производной dv/dk групповая скорость
говорят, что среда обладает нормальной
дисперсией, а во втором — аномальной. В оптике
осуществляются оба эти случая. Так, в вакууме

Возникает вопрос: какая же из этих скоростей
измеряется на опыте при определении, например,
скорости света. Анализ различных методов
измерения скорости света показывает, что ни
один из них не дает возможности определить
фазовую скорость, но все они дают групповую
скорость.
Из сказанного следует, что фазовая скорость в
точном соответствии со своим названием дает
лишь скорость перемещения определенной фазы
и, как показывает более строгий анализ,
совершенно не связана, например, со скоростью
движения фронта ограниченного в пространстве
пакета волн (сигнала) или со скоростью движения
энергии волны, которые определяются как раз
групповой скоростью.
Именно поэтому возникновение фазовой
скорости, большей скорости света в пустоте с, ни
в коем случае не противоречит утверждению
теории относительности (см. следующую лекцию)
о том, что скорость света в пустоте есть
предельная скорость.
В частности, в оптике доказывается, что
скорость фронта волны при любых условиях
равна с, т.е. скорости света в пустоте.
Лекция 8. КИНЕМАТИКА СПЕЦИАЛЬНОЙ ТЕОРИИ
ОТНОСИТЕЛЬНОСТИ (СТО)
Постулаты СТО; преобразования Лоренца; следствия из преобразований
Лоренца.
 1. Постулаты СТО.
1. Постулаты СТО.
Как уже говорилось в лекции 1, законы
ньютоновской (классической) механики
становятся неприменимыми при изучении
движения частиц, скорости v которых сравнимы
со скоростью света в пустоте с =3 108 м/с. В этом
случае следует использовать законы так
называемой специальной теории
относительности (СТО), созданной
А. Эйнштейном в 1905 году. В основе СТО лежат
два постулата.
Постулат относительности.
Все явления природы (механические,
электромагнитные, оптические и т. д.) протекают
одинаково во всех инерциальных системах
отсчета (ИСО), то есть все законы природы
выглядят одинаково во всех инерциальных
системах отсчета. Данный постулат является
обобщением принципа относительности Галилея,
относящегося только к механическим явлениям,
на все явления природы.
Популярное:

