Постулат постоянства скорости света.

Скорость света в пустоте одинакова во всех
системах отсчета, независимо от относительного
движения источника света и наблюдателя. Следует
отметить, что этот постулат подтвержден
многочисленными тонкими экспериментами.

В классической механике для перехода от
одной ИСО к другой, движущейся равномерно
относительно первой, используются так
называемые преобразования Галилея.

Рассмотрим две декартовы прямоугольные
системы координат K(x, y, z) и K'(x', y', z') (рис.
8.1). Пусть их оси ОХ и ОХ' совпадают и
положим, что система К' равномерно движется со

какой —либо точки Р в К и К' связаны
соотношениями:

К этим трем соотношениям следует добавить
еще соотношение для времени: время в обеих
системах с точки зрения классической механики

топот плиняклип тп с*сти

Формулы (8.1) и (8.2) представляют собой
имеющие место в ньютоновской механике так
называемые преобразования Галилея. Легко
убедиться, что уравнения ньютоновской механики
не изменяют своего вида при замене координат и
времени согласно этим формулам, или, как
говорят, уравнения механики Ньютона
инвариантны относительно преобразований
Галилея, то есть законы механики Ньютона
выглядят одинаково во всех ИСО.

В самом деле, напишем второй закон Ньютона
для частицы m в проекции на ось ОХ' системы К':

Дифференцируем первое соотношение (8.1) по
времени t':

или

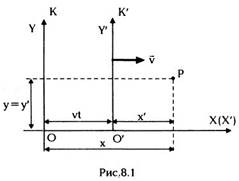
скоростью v относительно К вдоль оси ОХ,
причем в момент t = 0 их начала координат О и О'
совпадают. Совершенно очевидно, что координаты

Это известная теорема сложения скоростей в
механике Ньютона.

Дифференцируя (8.4) второй раз, получим

Итак, левые части ньютоновских уравнений не
меняются при преобразованиях Галилея. В правых
же частях этих уравнений стоят компоненты
силы, зависящие только от расстояний которые не
меняются при использовании преобразований
Галилея.

Действительно, расстояние между любыми
двумя точками A(x', y', z') и B(x', y', z')

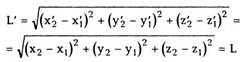
Подставляя (8.5) и (8.6) в (8.3), получим:

одинаково во всех ИСО, если использовать
преобразования Галилея. Поэтому эти
преобразования не меняют компонентов сил, то
есть

то есть преобразования Галилея не меняют
ньютоновских уравнений движения, или, как
говорят, эти уравнения инвариантны относительно
преобразований Галилея, что является
математической формулировкой принципа
относительности Галилея: законы механики
выглядят одинаково во всех ИСО.

Первый постулат СТО согласуется с этим
принципом и обобщает принцип относительности
на другие явления, в частности, на законы
распространения света. Однако одновременное
применение обоих постулатов СТО находится в
противоречии с преобразованиями Галилея. В
самом деле, если применить теорему сложения
скоростей (8.4) к свету, то получается, что, если
скорость света в системе К равна с, то в системе
К' она должна быть равна с' = с —v, что
противоречит второму постулату СТО.

Так как, однако, оба эти постулата
подтверждаются всеми известными

экспериментальными фактами, то противоречие
имеется не между постулатами, а между
постулатами и преобразованиями Галилея: эти
преобразования неприменимы к распространению
света и к движениям со скоростями, близкими к
скорости света, то есть " очевидные"
преобразования Галилея следует заменить
новыми, но такими, чтобы они переходили в
преобразования Галилея при движениях со
скоростями v « с.

2. Преобразования Лоренца.

Эйнштейну удалось получить такие
преобразования, но для этого ему пришлось
отказаться от привычных представлений о
пространстве и времени. Так, согласно
Эйнштейну, время не является абсолютным
понятием, а течет по разному в разных ИСО (tVt).
Эти преобразования имеют следующий вид:

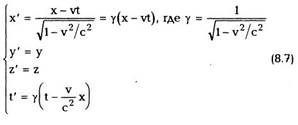
условиях, когда верна механика Ньютона,
преобразования (8.3) автоматически переходят в
преобразования Галилея (8.1) Выразим теперь из
(8.7) x, y, z, t через x', y', z', t' (обратные
преобразования). Получаем:

Преобразования (8.7) и (8.8) называются
преобразованиями Лоренца, который нашел их
ранее, но чисто формальным путем. Дело в том,
что до создания СТО английским физиком
Д. Максвеллом была написана система уравнений,
описывающая электромагнитные и оптические
явления (уравнения Максвелла). Из этих
уравнений следовало, что свет в пустоте должен
распространяться со скоростью с в любой ИСО,
однако сами уравнения Максвелла оказались не
инвариантными относительно преобразований
Галилея. Лоренц же чисто формальным путем
нашел преобразования, относительно которых
уравнения Максвелла оказываются

инвариантными.

Произведем теперь переход от системы К к системе К', воспользовавшись преобразованиями Лоренца (8.8):

Мы не будем выводить преобразования
Лоренца, но для оправдания покажем, что именно
они обеспечивают отсутствие противоречия
между обоими постулатами СТО. Рассмотрим для
этого снова две ИСО К и К'. Предположим, что в
момент t = 0, когда начала О и О' систем К и К'
совпадают, в точке О (и О') происходит вспышка
света. Через время t свет распространяется в
системе К на расстояние ct и достигает
сферической поверхности с радиусом R = ct,
уравнение которой имеет вид

то есть снова получаем уравнение сферической
поверхности, но с центром в О'. Мы видим, что
благодаря преобразованиям Лоренца и
постоянству скорости света удовлетворяется и
первый постулат относительности: волна,
выходящая из общего начала координат при t = 0,
остается сферической как в системе К, так и в
системе К' относительно О'. На первый взгляд
кажется непонятным, каким образом

геометрическое место точек (сфера с центром в
О'), которых достигает свет в системе К', остается
сферой с центром в О в системе К. Этот

кажущийся парадокс связан с тем, что события,
одновременные в одной системе отсчета, не будут
одновременными в другой.

Найдем теперь, используя преобразования
Лоренца, теорему сложения скоростей в СТО.
Берем дифференциал соотношений (8.7):

Деля первые три равенства на четвертое,
получим:

При v/c « 1 эти преобразования переходят в

теорему сложения скоростей Галилея.

Обратные преобразования получаются из (8.12)
простым изменением знака перед v, то есть

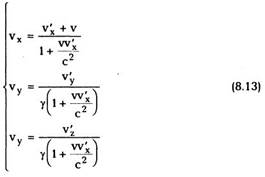
3. Следствия из преобразований
Лоренца.

а) Относительность одновременности.

В классической физике считалось, что два
события, которые произошли одновременно в
одной ИСО, будут одновременными и в другой

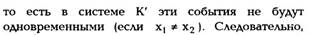
понятие одновременности в СТО является
понятием относительным.

б) Сокращение длины.

Имеется стержень, длина которого, измеренная
в той ИСО, где он покоится, равна Lq. Эта длина
называется собственной длиной. Пусть стержень
покоится в системе К' и расположен вдоль оси у'
или z', тогда его собственная длина

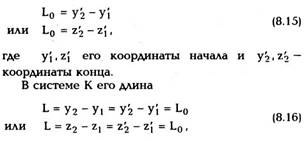
В системе К длина движущегося со скоростью v стержня

то есть поперечные движению стержня размеры
остаются неизменными. Если же стержень
расположен вдоль оси х' в системе К', то его
собственная длина

причем координаты х, и х ₂ необходимо измерить
одновременно по часам в системе К (то есть при

ti=t₂).

Подставляя преобразования Лоренца (8.7) в
(8.17), получим

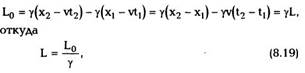
то есть продольные размеры движущегося
стержня сокращаются в у раз. Нетрудно показать,
что стержень, покоящийся в системе К, тоже
сокращается в у раз с точки зрения наблюдателя,
находящегося в системе К'.

в) Замедление хода времени.

Промежуток времени между этими же событиями в системе К

Промежуток времени между двумя
последовательными событиями, происшедшими в
одной точке пространства и измеренный по
неподвижным часам, расположенным в этой
точке, называется собственным промежутком

то есть с точки зрения наблюдателя в системе К
движущиеся часы (те, что покоятся в системе К')
идут в у раз медленней. Опять же нетрудно
показать, что с точки зрения наблюдателя в
системе К' идут медленнее те часы, которые
покоятся в системе К.

Рассмотрим в заключение некоторые примеры
сложения скоростей в СТО.

Пусть в системе К' движется частица вдоль
оси х' со скоростью v'_x = 0.9с, а сама система К'
движется относительно К со скоростью v = 0.9с.
Какова скорость этой частицы в системе К?

Согласно преобразований Галилея скорость
частицы v_x = v'_x + v = 1.8с > с. Из преобразований
Лоренца (8.13)

Пусть теперь в системе К' движется вдоль х'
свет со скоростью v'_x = с. Его скорость в системе

постулатом СТО, согласно которому скорость
света одинакова во всех инерциальных системах
отсчета.

Лекция 9. ДИНАМИКА СТО

Второй закон Ньютона в СТО; энергия свободной частицы; связь энергии и
импульса; эквивалентность энергии и массы.

Второй закон Ньютона в СТО.

Перейдем теперь к рассмотрению динамики
материальной точки (частицы) в теории
относительности.

Прежде всего заметим, что закон инерции
(первый закон Ньютона) является инвариантным
относительно преобразований Лоренца.

Действительно, если в некоторой ИСО К частица
движется с постоянной скоростью, то и в любой
другой системе К' скорость частицы согласно
преобразований Лоренца останется постоянной.
Второй же закон Ньютона, как мы знаем,
инвариантен относительно преобразований
Галилея, поэтому, согласно Эйнштейну, его
следуем так изменить, чтобы он стал
инвариантным относительно преобразований
Лоренца.

но изменить ньютоновское определение импульса

Оказывается, этого можно добиться, если
записать второй закон Ньютона через импульс
частицы р в классической форме (см. лекцию 2,
соотношение (2.8))

Следует отметить, что при выводе выражения
(9.2) исходили из требования выполнения закона
сохранения импульса для системы релятивистских
частиц.

Если частица движется со скоростью v< < c,
соотношение (9.2) переходит в классическое.

покоилась в начале координат при t = 0, начала
действовать постоянная сила f = [f, 0, 0},

направленная вдоль оси ОХ. Найти скорость
частицы в зависимости от времени t.

Предыдущая 1 2 3 4 5 6 789 Следующая