Построение картины зацепления

ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКСКИЙ УНИВЕРСИТЕТ

Кафедра «теории механизмов и машин»

Допускаю к защите_______________

подпись

Руководитель Кузнецов Н.К.

И.О.Фамилия

Разработка автоматизированной системы кинематического и силового анализа рычажного механизма

наименование темы

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе по дисциплине

Теория механизмов и машин

Выполнил студент группы ММб-14-1 О.В.Бажина __________

шифр группы И.О. Фамилия подпись

Нормоконтроль __________

подпись

Курсовая работа защищена с оценкой _______________________________

Иркутск 2016 г.

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ЗАДАНИЕ

НА КУРСОВОЕ ПРОЕКТИРОВАНИЕ

По курсу Теория машин и механизмов

Студенту Бажиной О.В.

Тема проекта: Разработка автоматизированной системы кинематического и силового анализа рычажного механизма

Исходные данные:

Проект 1 Вариант 1

Рекомендуемая литература:

1. Артоболевский И.И.Теория механизмов и машин: учебник для втузов. - 6-е изд., стер. - М.: ООО ТИД «Альянс», 2011. - 640с.

2. Курсовое проектирование по теории механизмов и машин: учебное пособие/ А.С.Кореняко [и др.]. – Репринт. изд.– М.: МедиаСтар, 2012. – 330с.

3. Кузнецов Н.К. Теория механизмов и машин: учеб. пособие. – Иркутск: Изд-во ИрГТУ, 2014. – 104 с.

4. Шматкова А.В.Теория механизмов и машин: учеб. пособие. – Иркутск: Изд-во ИрГТУ, 2014. – 160 с.

Графическая часть на листах.

Дата выдачи задания___ 2016 г.

Задание получил О.В. Бажина (И.О. Фамилия)

Дата представления проекта руководителю 2016 г.

Руководитель курсового проектирования Н.К. Кузнецов

Содержание

1. Введение. 4

2. Построение картины зацепления. 5

3. Напряжения в опасных сечениях зуба. 8

3.1 Допускаемые напряжения. 8

3.2............ Приведенный радиус кривизны соприкасающихся эвольвент. 10

3.3 Условное напряжение как критерий качества зубчатого зацепления. 13

3.4 Касательные напряжения в следствии сдвига вершин зубьев шестерни и зубчатого 15

4. Параметры внешнего эвольвентного зацепления зубчатых колёс. 16

4.1 Положение отрезка активного зацепления. 18

4.2 Определение окружной толщины вершины зубьев. 20

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ.. 23

Введение

В наши дни, в эпоху компьютеров и информационных технологий, на первый план выходят аналитические методы решения задач, которые хорошо укладываются в общепринятые сейчас способы исследования и проектирования машин.

Любое зубчатое зацепление можно нарисовать с помощью инструментов. А все, что можно нарисовать, можно сделать аналитически. Но наш метод позволяет не только нарисовать, но и спроектировать любое зубчатое зацепление с оптимальным сочетанием параметров.

Напряжения в опасных сечениях зуба

В результате приложении силы к зубьям, они деформируются, и в теле зубьев возникают напряжения. Судя по статистике разрушений зубьев зубчатых колёс зубчатых передач, наибольшую опасность представляют контактные напряжения .Наибольшее значение контактных напряжений наблюдается в моменты входа и выхода зубьев из зацепления. Ввиду неблагоприятных условий для образования смазочного слоя, опасными являются напряжения на начальной линии зубьевТакже опасными являются напряжения вследствие изгиба зуба , максимальное значение которых в большинстве случаев наблюдается на переходной поверхности зуба.

При малой толщине вершины зуба его могут разрушить напряжения , появляющиеся в результате сдвига. Такое разрушение именуется срезом вершины зуба.

Таким образом, при проектировании зуба нужно учитывать три вида напряжений: нормальное контактное напряжение , нормальное напряжение вследствие изгиба и касательное напряжение среза .

Допускаемые напряжения

При проектировании зубчатого зацепления, обычно, считаются известными условия его работы, а также предполагаемый материал и обработка зубчатых колёс. Это позволяет установить допускаемые напряжения , , , которых не должны превышать максимальные напряжения в опасных сечениях зубьев

, , . (1.1)

Где - Максимальное напряжения изгиба-( FS так как F – изгиб, S – сжатие.)

Рис. 3. Зуб эвольвентного зацепления при срезе

зуб

- Максимальное напряжения сдвига

- Максимальные контактные напряжения

Введём коэффициенты запаса прочности по рассматриваемым напряжениям следующим образом

, , . (1.2)

Наибольшее контактное напряжение наблюдается по средней линии контакта

, (1.3)

где - дополняющее напряжение(размерность напряжения, потому что в формуле один параметр размерности напряжения, дополняет другой параметр размерности напряжения, а после вычисления квадратного корня получаем контактное напряжение); (1.4)

, – коэффициенты Пуассона материалов зубчатых колёс;

, – модули упругости материалов зубчатых колёс;

, (1.5)

– коэффициент, также имеющий размерность напряжения, но характеризующий передаваемое усилие и геометрию в ближайшей окрестности линии соприкосновения зубчатых колёс;

– ширина зуба, по которой распределено передаваемое усилие ;

– приведенный радиус кривизны на линии соприкосновения зубчатых колёс

В формуле (9.6) нужно приведённое напряжение, приведённое напряжение как бы усредняет кривизну сопряжённых поверхностей зубьев, вместо кривизны двух зубьев делает одну кривизну – приведённую. Именно так доказал Герц.

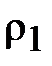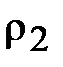Рис. 4. Радиусы кривизны эвольвент

ρ 1

ρ 2

–радиусы кривизны эвольвент

ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКСКИЙ УНИВЕРСИТЕТ

Кафедра «теории механизмов и машин»

Допускаю к защите_______________

подпись

Руководитель Кузнецов Н.К.

И.О.Фамилия

Разработка автоматизированной системы кинематического и силового анализа рычажного механизма

наименование темы

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе по дисциплине

Теория механизмов и машин

Выполнил студент группы ММб-14-1 О.В.Бажина __________

шифр группы И.О. Фамилия подпись

Нормоконтроль __________

подпись

Курсовая работа защищена с оценкой _______________________________

Иркутск 2016 г.

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ЗАДАНИЕ

НА КУРСОВОЕ ПРОЕКТИРОВАНИЕ

По курсу Теория машин и механизмов

Студенту Бажиной О.В.

Исходные данные:

Проект 1 Вариант 1

Рекомендуемая литература:

1. Артоболевский И.И.Теория механизмов и машин: учебник для втузов. - 6-е изд., стер. - М.: ООО ТИД «Альянс», 2011. - 640с.

3. Кузнецов Н.К. Теория механизмов и машин: учеб. пособие. – Иркутск: Изд-во ИрГТУ, 2014. – 104 с.

4. Шматкова А.В.Теория механизмов и машин: учеб. пособие. – Иркутск: Изд-во ИрГТУ, 2014. – 160 с.

Графическая часть на листах.

Дата выдачи задания___ 2016 г.

Задание получил О.В. Бажина (И.О. Фамилия)

Дата представления проекта руководителю 2016 г.

Руководитель курсового проектирования Н.К. Кузнецов

Содержание

1. Введение. 4

2. Построение картины зацепления. 5

3. Напряжения в опасных сечениях зуба. 8

3.1 Допускаемые напряжения. 8

3.2............ Приведенный радиус кривизны соприкасающихся эвольвент. 10

3.3 Условное напряжение как критерий качества зубчатого зацепления. 13

3.4 Касательные напряжения в следствии сдвига вершин зубьев шестерни и зубчатого 15

4. Параметры внешнего эвольвентного зацепления зубчатых колёс. 16

4.1 Положение отрезка активного зацепления. 18

4.2 Определение окружной толщины вершины зубьев. 20

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ.. 23

Введение

Построение картины зацепления

Построим основные окружности и из центров и , лежащих на расстоянии .

Проведём касательную к основным окружностям, пересекающую межосевую линию . Точка пересечения межосевой линии и касательной называется полюсом зацепления . Получившийся угол называют углом зацепления.

На касательной отметим отрезок возможного зацепления . Его длина .

Рис. 1. Основные окружности и отрезки на лини зацепления

На отрезке отметим:

· начало отрезка активного зацепления – точку , ;

· конец отрезка активного зацепления – точку , ;

· точку пересопряжения , .

Для длин получившихся отрезков должны выполняться соотношения:

· – длина отрезка активного зацепления;

· – нормированная длина отрезка активного зацепления;

· – коэффициент перекрытия.

предположим, что отрезок выбрали больше чем Pb на 1%. Конечно отрезок -это отрезок, на котором зубья могут соприкасаться, но выбираем больше чем Pb на 1%, так как если будет короче, то мы можем наблюдать, что один из зубьев из зацепления вышел, а второй еще не зашел. А если возьмем значение отрезка активного зацепления равным ровно Pb, то один зуб будет входить в тот момент, когда другой будет выходить.

Из центров и построим окружности вершин шестерни и зубчатого колеса . Они должны проходить через точки и .

Из этих же центров построим окружности впадин шестерни и зубчатого колеса . Окружности впадин должны касаться окружностей вершин, проведенных из противоположного центра.

Между окружностями впадин и вершин впоследствии будет построен зубчатый сектор.

Рис. 2. Схема построения контура зубьев шестерни и зубчатого колеса

Для начала между окружностями и построим две соседние эвольвенты зуба шестерни левого развёртывания, проходящие через точки и . Условно назовём эти точки изображающими точками.

Построение эвольвенты нужно начать с проведения нескольких касательных к основной окружности, пересекающих место, где будет эвольвента. Одна из этих касательных должна проходить через изображающую точку. Касательную, проходящую через изображающую точку, назовём начальной.

Рассмотрим пример с построением эвольвенты, проходящей через точку . Отрезок начальной касательной назовём начальным.

Пусть соседняя касательная касается окружности в точке , а эвольвенту пересекает в точке . Поскольку эвольвента может быть начерчена изображающей точкой , находящейся на разматываемой нерастяжимой нити, то длина отрезка будет состоять из длины отрезка и длины дуги . Используя это правило, при помощи транспортира, калькулятора и линейки далее будем строить все эвольвенты зубьев.

Отметим дальнюю точку эвольвенты зуба шестерни, проходящей через точку , и назовём её .

Построим две эвольвенты зуба колеса левого развёртывания между окружностями и , также проходящие через точки и . Точка будет дальней точкой эвольвенты зуба колеса.

Из дальних точек и по окружностям и отложим навстречу друг другу дуги вершин зубьев , и поставим на их концах точки и . , .

Из точек и построим эвольвенты зубьев колеса и шестерни правого развёртывания. При правильном расчёте и построении эти две эвольвенты должны коснуться друг друга в точке , лежащей на инверсной линии зацепления[1]. В зубчатом зацеплении с боковым зазором между ними должен быть планируемый боковой зазор.

Две пары построенных эвольвент вместе с дугами , образуют дальние части контуров зубьев колеса и шестерни. На рисунке эти контуры вместе с характерными точками отмечены пунктирными стрелками.

1. Ближняя к оси вращения часть контура зуба образована удлинёнными эвольвентами, сопряжёнными с основными эвольвентами и окружностями впадин и . Приближённо их можно заменить дугами окружности, сопряжёнными с эвольвентами на удалении от центров вращения на расстоянии и с дальней стороны. С ближней стороны сопряжение дуг окружности должно осуществляться с окружностями впадин и .