Размещение разногабаритных элементов
Рассмотренные ранее алгоритмы не учитывали габариты размещаемых элементов. Задача размещения существенно усложняется при необходимости размещения разногабаритных элементов на плате при нефиксированных позициях для установки элементов.
Различают размещение элементов кратных габаритов и некратных габаритов (существенно разногабаритных).
В первом случае задача сводится к целочисленной задаче размещения с ограничением, при котором один элемент может занимать несколько позиций (рис. 6.13 (а)) или в одну позицию может быть помещено несколько элементов (рис. 6.13 (б)).
Задача размещения существенно разногабаритных элементов имеет сходство с известной задачей о раскрое материала, т. к. в обоих случаях возникает требование эффективного использования площади. Однако математически обе задачи формулируются по-разному: эффективное использование площади является функционалом для задачи о раскрое и ограничением для задачи размещения. Функционалом задачи размещения может служить СДС.
Рисунок 6.13. Разногабаритные элементы с кратными габаритами, занимающими несколько позиций (а) или – часть позиции (б)
Рассмотрим алгоритм нисходящего проектирования размещения разногабаритных элементов, основанный на последовательном разбиении КП. Алгоритм является вариантом алгоритма дихотомического деления.
Пусть задано множество элементов E={e1, e2, …, em} с размерами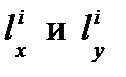 
. Вначале рассчитываются размеры поля для размещения элементов
Далее множество элементов разбивается на две малосвязанные группы с помощью одного из алгоритмов компоновки. Особенностью является то, что в качестве ограничения размера группы выступает суммарная площадь входящих в нее элементов. Обозначим через S(E1) и S(E2) суммарные площади элементов, входящих в группы E1 и E2. Тогда
S(E1) + S(E2) = S(E) и |S(E1) - S(E2)| £ С, где С – заданный параметр.
Проведем вертикальный разрез КП таким образом, чтобы площади левой и правой частей были равны соответственно S(E1) и S(E2). Координата разреза
х= S(E1)/Ly.
На следующем шаге аналогичная процедура применяется к группам элементов E1 и E2, однако теперь уже проводятся горизонтальные разрезы.
Процесс разбиения продолжается до тех пор, пока каждая из полученных групп не будет состоять из одного элемента. Пример размещения разногабаритных элементов приведен на рис. 6.14.
Рисунок 6.14. Размещение, полученное методом дихотомического деления
Алгоритмы трассировки межсоединений
Трассировка монтажных соединений - это задача геометрического построения на КП всех цепей данной конструкции, координаты начала и конца которых определены при размещении элементов. Следовательно, задача трассировкисостоит в отыскании геометрически определенного способа соединений эквипотенциальных выводов схемы.
При этом необходимо учитывать различные конструктивно-технические ограничения: допускаются пересечения или нет, возможен ли переход с одного слоя на другой, сколько слоев отводится для трассировки, допустимые ширина проводников и расстояния между ними и т. д.
Алгоритмы трассировки существенно зависят от принятой конструкции и технологии изготовления электронной аппаратуры.
В табл. 7.1. приведены основные критерии трассировки в зависимости от технологии изготовления.
Таблица 7.1. Критерии трассировки межсоединений
| Технология изготовления
| Критерии
|
| Проводной монтах
| СДС, максимальная длина связи
|
| ДПП, МПП (МСО)
| СДС, число переходных отверстий
|
| МПП (ОКП)
| СДС, число слоев
|
| ГИС
| число пересечений проводников, площадь кристалла
|
| ИС, БИС, СБИС
| число пересечений проводников, площадь кристалла, число межслойных переходов
|
ДПП – двусторонние печатные платы; МПП – многослойные ПП; МСО - металлизация сквозных отверстий; ОКП – открытые контактные площадки; ГИС – гибридные интегральные схемы.
Этап трассировки является одним из самых трудоемких этапов конструкторского проектирования электронной аппаратуры.
Задачу трассировки можно условно представить в виде четырех последовательно выполняемых этапов, отвечающих на вопросы:
A. Что? (Определение перечня соединений);
B.Где? (Распределение соединений по слоям);
C.Когда? (Определение порядка проведения соединений);
D. Как? (Трассировка проводников).
А. На первом этапе формируется точный список, указывающий, какие соединения (цепи или фрагменты цепей схемы) должны быть проведены. Для решения этой задачи используют алгоритмы построения минимальных связывающих деревьев (МСД).
Популярное:
