Задачи, близкие к задаче о кратчайшем пути

1. Наиболее надежный путь.

В этом случае вес ребра представляет его надежность. Надежность пути от s к t, составленного из ребер, взятых из множества P, задается формулой

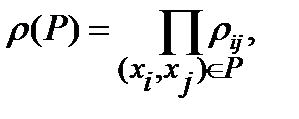где ρ _ij – надежность ребра (x_i_,x_j).

2. Самый длинный (критический) путь.

Задача сетевого планирования, заключающаяся в нахождении самого длинного по временной протяженности пути в сетевом графике, определяющего продолжительность работ по выполнению проекта.

3. Путь с наибольшей пропускной способностью.

В этом случае каждое ребро графа имеет пропускную способность q_ij и требуется найти путь от s к t с наибольшей пропускной способностью. Пропускная способность пути P определяется ребром из P с наименьшей пропускной способностью, т.е.

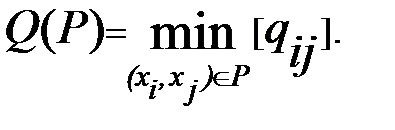
Определение. Если множество вершин графа G(X, U) разбить на два подмножества Х₁ и Х₂ (где Х=Х₁ È Х₂), то множество ребер графа, одни концевые вершины которых лежат в Х₁, а другие в Х₂, называется разрезом графа G.

Теорема Форда – Фалкерсона (1955, L.R. Ford, D.R. Fulkerson). Пропускная способность пути с наибольшей пропускной способностью от s к t равна

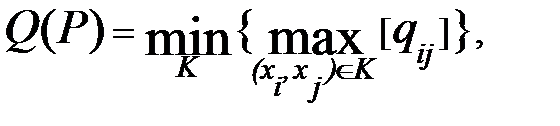
где К – любой (s-t) разрез.

Для нахождения пути с наибольшей пропускной способностью в неографе предложен следующий алгоритм.

Алгоритм Франка – Фриша

Алгоритм Франка-Фриша (G. Frank, I. Frisch) заключается в следующем.

1. Взять (s-t) разрез К₁ = ({s}, X\{s}) и найти

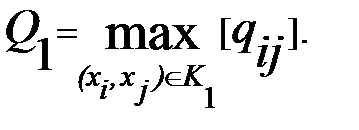
2. Закоротить все ребра графа (x_i_,x_j) с q_ij≥ Q₁, т.е. заменить вершины x_i и x_j на вершину х, удалив ребро (x_i_,x_j), положить Гх=Гx_i È Гx_j.

3. Для полученного графа G₁ выбрать другой (s-t) разрез К₂ и найти

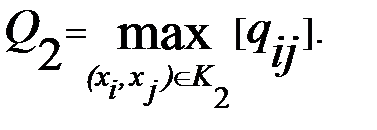
4. Закоротить все ребра графа (x_i_,x_j) с q_ij≥ Q_2. Получить граф G₂ … и т.д., пока не будут объединены вершины s-t.

5. Теперь каждый (s-t) путь в графе G^', образованный вершинами из G и теми ребрами, которые оказались закороченными, будет иметь максимальную пропускную способность.

Пример. Найти (s-t) путь с наибольшей пропускной способностью в графе G(X, U) (рис. 7.8).

x₁

x₂

x₃

x₄

x₅

x₆

x₇

x₈

x₉

x₁₀

x₁₁

x₁₂

Рисунок 7.8. Исходный граф

1. Проводим разрез К₁ = ({s}, X \{s}) (рис. 7.9).

x₁

x₂

x₃

x₄

x₅

x₆

x₇

x₈

x₉

x₁₀

x₁₁

x₁₂

К₁

Рисунок 7.9. Разрез К₁

2. Находим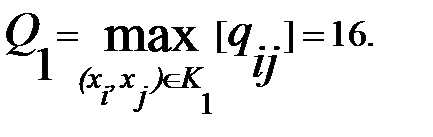

3. Закорачиваем все ребра графа (x_i_,x_j) с q_ij≥ Q₁.

4. Это ребра (s_,x₄), (x_3,x₆), (x_5,x₈), (x_6,x₉) и (x_7,x₁₂). Получаем граф G₁ (рис. 7.10).

s, х₄

x₁

x₂

x₃, х₆, х₉

x₇, х₁₂

x₁₀

x₁₁

10, 14

13, 7

6, 9

13, 7

7, 9

К₂

x₅, х₈

Рисунок 7.10. Разрез К₂

5. 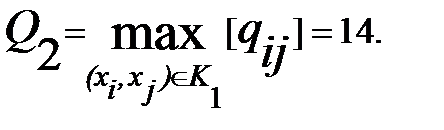Проводим разрез К₂, находим

6. Закорачиваем все ребра графа (x_i_,x_j) с q_ij≥ Q₂. Это ребра (s_,x₄, х₄, х₆, х₉), (x_3,x₆), (х₁, х₂, x_5,x₈, t). Получаем граф G₂ (рис. 7.11).

7. 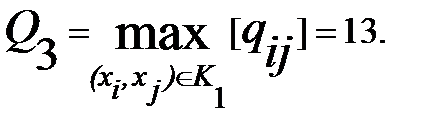Проводим разрез К₃, находим

x₁, x₂, x₅, х₈, t

x₇, х₁₂

x₁₀

x₁₁

6 10

6 7

13 7

4, 6, 9

13, 7

9, 7

К₃

s, х₄, x₃, х₆, х₉

Рисунок 7.11. Разрез К₃

8. Закорачиваем все ребра графа (x_i_,x_j) с q_ij ≥ Q₃. Получаем граф G₃ (рис. 7.12).

s, х₄, x₃, х₆, х₉, x₁, x₂, x₅, х₈, t

x₇, х₁₂

x₁₀

x₁₁

6, 8, 10

6, 8, 9 7

4, 6, 9, 10

7, 12

8, 11

Рисунок 7.12. Окончательный граф

9. Вершины s-t объединены. Пропускная способность искомого пути Q(P)=13.

10. Строим граф, вершины которого – вершины исходного графа G, а ребра – ребра с пропускной способностью q_ij ≥ Q(P)=13.

На рисунке 7.13 показан путь с наибольшей пропускной способностью.

x₁

x₂

x₃

x₄

x₅

x₆

x₇

x₁₀

x₁₁

x₁₂

Рисунок 7.13. Путь с наибольшей пропускной способностью.

Задача Штейнера

Виды используемых деревьев определяются технологией выполнения соединений и схемотехническими требованиями. При автоматизированном конструировании схем проводного и печатного монтажа ставятся разные задачи построения минимальных деревьев соединений. В первом случае не допускается вводить дополнительные вершины (соединение «контакт» - «контакт»). Для решения такой задачи используют рассмотренные ранее эффективные алгоритмы Краскала, Прима и другие. Во втором случае разрешается вводить дополнительные вершины и соединяющие их ребра (соединения «контакт» - «проводник», «проводник» - «проводник»). Такая задача называется задачей Штейнера (J. ), деревья соединений – деревьями Штейнера (ДШ), а дополнительные вершины – точками Штейнера (ТШ).

Задача построения дерева Штейнера имеет следующий вид. Требуется найти такой связный ациклический граф с использованием дополнительных вершин Штейнера (дерево Штейнера) Т’ = (Х’, U’), что Х’ включает все вершины Х и дополнительные вершины (вершины Штейнера) и суммарный вес ребер в T’ будет минимальным. На рис. 7.14 (а) показано МСД, суммарная длина ребер - 10, 123, а на рис. 7.14 (б) – дерево Штейнера, суммарная длина ребер – 9, 196.

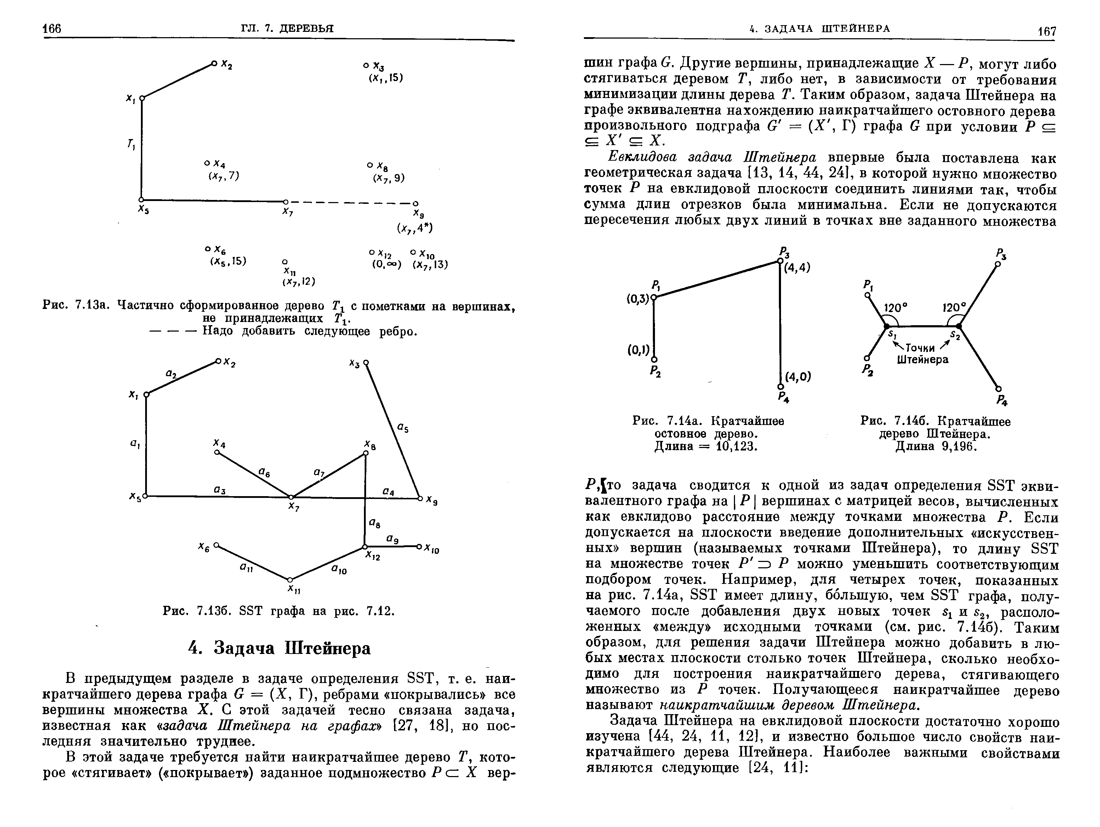
Рисунок 7.14. МСД (а) и дерево Штейнера (б)

Задача о соединении точек оптимальным образом – одна из старейших оптимизационных задач. Она восходит еще к П. Ферма (Pierre de Fermat). Еще в ХVII столетии была предложена следующая задача. На плоскости найти такую точку Р, которая минимизирует суммарное расстояние от Р до трех заданных точек плоскости. Ферма, Торричелли (E. Torricelli) и Кавальери (B.F. Cavalieri) независимо друг от друга нашли решение этой задачи.

Общим решением этой задачи является следующее. Точка Р либолежит внутри треугольника, построенного на заданных точках, либо совпадает с одной из этих точек. В первом случае каждый из углов между отрезками, соединяющими Р с каждой их точек, составляет 120⁰. Во втором случае угол, образованный отрезками, соединяющими эту точку с другими заданными точками, равен или больше 120⁰. Рис. 7.15. демонстрирует способ решения задачи, найденный в середине ХVII века.

Для отыскания точки Р, ближайшей (в смысле суммарного расстояния) к заданным точкам А, B, C, сначала строится треугольник (АBC) и на одной из его сторон, например на АC, строится равносторонний треугольник. (АBХ) так, что точка В лежит вне этого треугольника. Точка пересечения окружности, описанной вокруг равностороннего треугольника (АBХ), с отрезком (BХ) есть искомая точка Р.

Точкой Торричелли треугольника (ABC) называется такая точка Р, из которой стороны данного треугольника видны под углом 120⁰, т.е. углы Ð AРB, Ð AРC и Ð BРC равны 120⁰.

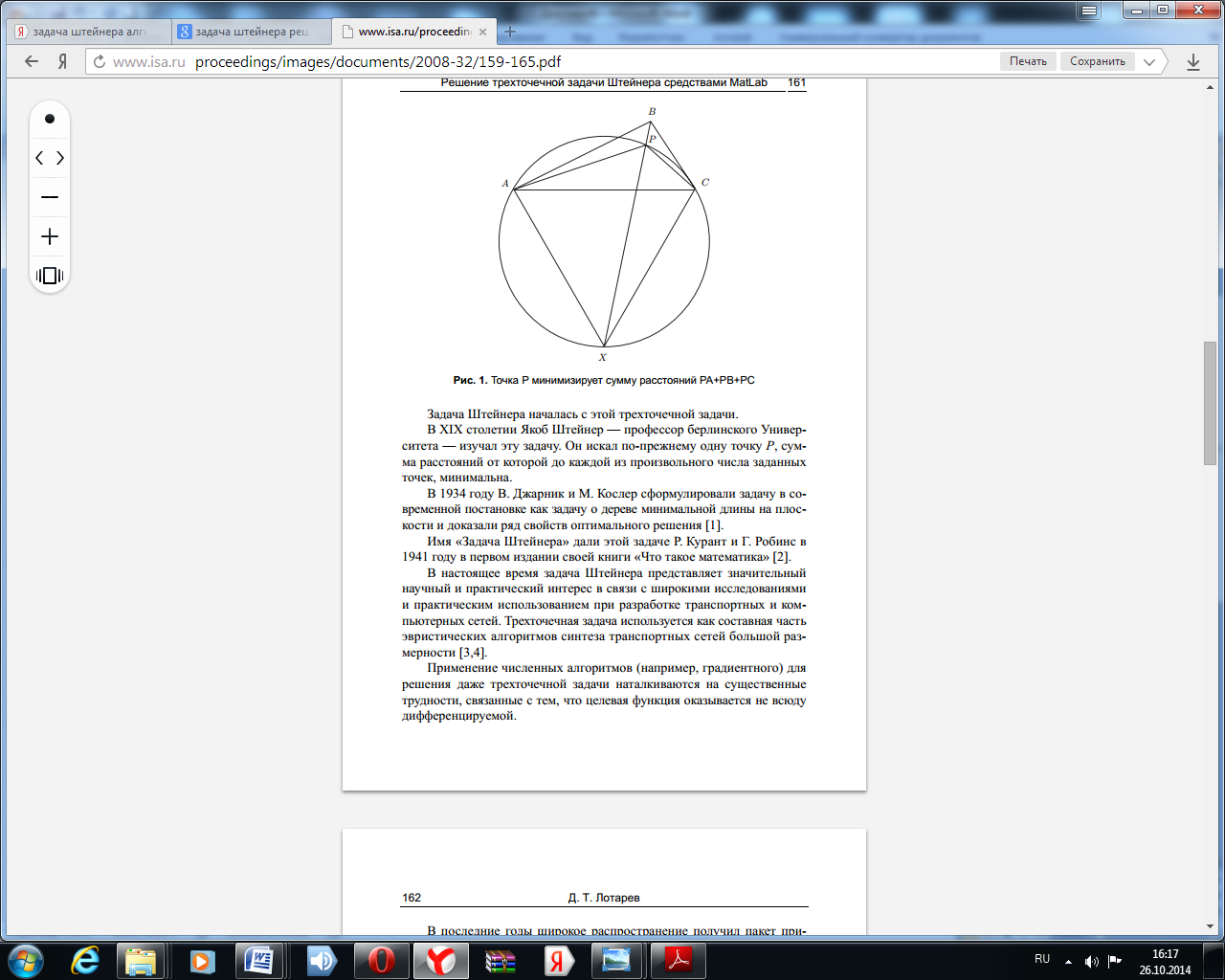
Рисунок 7.15. Нахождение точки Торричелли

Трехточечная задача используется как составная часть алгоритмов решения задачи Штейнера.

Перебираем тройки вершин графа и находим точки Торричелли. Выбираем такие точки, включение которых в дерево даст максимальный эффект.

Задача Штейнера относится к классу так называемых NP-полных задач, поэтому алгоритмы, дающие точные решения, как правило, не могут быть использованы в САПР из-за неприемлемой временной сложности. Это обстоятельство послужило стимулом для разработки многочисленных эвристических алгоритмов. Наибольший практический интерес представляет алгоритм последовательного введения дополнительных вершин в дерево Прима-Краскала.

Возможно, наиболее важным практическим применением задачи Штейнера является конструирование интегральных электронных схем. Более короткая сеть проводящих линий на интегральной схеме требует меньшего времени зарядки-разрядки по сравнению с более длинной сетью и повышает, таким образом, быстродействие схемы. Однако задача отыскания кратчайшей сети на интегральной схеме имеет другую геометрию, так как проводники на ней обычно проходят лишь в двух направлениях — горизонтальном и вертикальном. Такая задача получила название прямоугольной задачи Штейнера.

Для случая ортогональной метрики доказано, что если через каждую точку из исходного множества точек провести горизонтальные и вертикальные линии, то решение задачи Штейнера можно получить, рассматривая в качестве возможных дополнительных вершин только точки пересечения полученной сетки линий (рис.7.16 (а)).

Алгоритм последовательно вводит в текущее дерево Прима-Краскала каждую из дополнительных вершин решеточного графа, строит новое дерево Прима и запоминает полученный выигрыш в длине. После оценки всех дополнительных точек в текущее дерево включается точка с максимальным выигрышем (рис.7.16 (б)). При этом, чтобы избежать в процессе преобразования появления избыточных точек, необходимо учитывать, что дополнительные точки в дереве Штейнера могут иметь только степень 3 и 4.

Точки Штейнера

Возможные точки Штейнера

Р₁

Р₂

Р₃

Р₄

Р₅

Р₆

Точки Штейнера

Возможные точки Штейнера

Р₁

Р₂

Р₃

Р₄

Р₅

Р₆

Рисунок 7.16. Кратчайшие остовное дерево (а) (L = 18)

и дерево Штейнера (б) (L = 15)

Рассмотрим некоторые эвристические методы построения деревьев Штейнера.

Метод Ханана

Метод Ханана (M. Hanan) заключается с следующем.

1. Все множество вершин с координатами s разбивается на классы S₁, S₂, ..., S_m в порядке неубываниякоординаты s_i так, чтобы у всех вершин одного класса была одинаковая координата s.

2. Анализируется множество вершин класса S₁ и соединяется между собой прямой.

3. Образуется множество I, состоящее из вершин, включенных в дерево и точек, принадлежащих построенной прямой.

4. Выбирается следующее множество S_i₊₁, имеющее наименьшую координату s. Для вершины x_kÎ S_i₊₁ определяется точка x_j, для которой d_kj = min{d_kg} x_gÎ I. Вершина x_k соединяется двухзвенной ломаной линией с точкой x_jÎ I.

5. Для очередной вершины класса S_i₊₁ операция подсоединения к дереву выполняется в соответствии с пунктами 3, 4.

6. Пункты 3, 4, 5 повторяются для всех множеств S_i до построения полного дерева.

Рассмотрим пример построения дерева Штейнера по методу Ханана для вершин, представленных на рис. 7.17 (а).

1. Разобьем множество вершин X = {x₁, x₂, ..., x₅} на классы по неубыванию координаты s_i, получим: S₁={x₁}, S₂={x_2,x₃}, S₃={x₄}, S₄={x₅}.

2. В классе S₁ всего одна вершина, поэтому соединение вершин не производим.

3. Вершину x₂Î S₂ соединяем с x₁ двухзвенной ломаной линией, причем сначала в направлении перпендикулярном оси s, а затем оси t.

4. Вершину x₃Î S₂ соединяем с ближайшей точкой уже построенного фрагмента.

5. Переходим в следующий класс и x₄Î S₃соединяем с ближайшей точкой дерева, получаем ТШ 1.

6. Вершину x₅Î S₄ соединяем по кратчайшему расстоянию с ближайшей точкой построенного дерева, получаем ТШ 2.

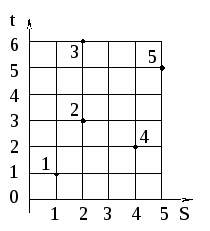Результат построения дерева Штейнера с суммарной длиной ребер L=11 представлен на рис. 7.17 (б).

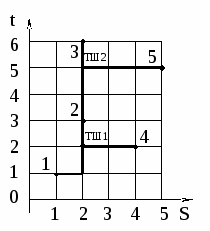
Рисунок 7.17. Вершины графа (а); дерево Штейнера (метод Ханана) (б)

Столб Штейнера

Метод " Столб Штейнера" является одним из наиболее эффективных по времени реализации эвристических алгоритмов построения дерева Штейнера и предусматривает следующий порядок действия.

1. Все вершины проецируются на ось s.

2. Расстояние от наименьшей до наибольшей координаты s делится пополам, и из этой точки проводится перпендикуляр (столб Штейнера).

3. Из каждой вершины опускается перпендикуляр до пересечения со столбом Штейнера.

Рассмотрим пример построения дерева Штейнера по данному методу для представленного на рис. 7.17 (а) множества вершин.

1. Находим среди множества проекций на ось s (s₁=1, s₂= s₃=2, s₄=4, s₅=5) минимальное и максимальное значения: mins_i = s₁= 1, maxs_i = s₅= 5.

2. Вычисляем координату проведения столба Штейнера: s_i = (s₁ + s₅) / 2 = 3.

3. Проводим столб Штейнера с координатой s_i = 3 и опускаем из всех вершин перпендикуляры до пересечения со столбом.

Результат построения дерева Штейнера с суммарной длиной ребер L=12 представлен на рис. 7.18 (а).

Аналогично строится горизонтальный столб (рис. 7.18 (б)), L=12.

Рисунок 7.18. Деревья Штейнера, построенные методом " Столб Штейнера", (

а) – вертикальный; (б) – горизонтальный столбы

Временная сложность алгоритма О(n²).

В. На втором этапе предпринимается попытка точно решить, на каком слое каждое соединение может располагаться.

Расслоение можно проводить до, после или во время трассировки отдельных соединений. Расслоение основано на анализе схемы соединений для выявления конфликтующих проводников.

Если расслоение проводится до собственно трассировки, то для контактов каждой цепи строится минимальный охватывающий прямоугольник. Строится граф перекрытий прямоугольников, вершины которого цепи, а ребра между вершинами проводятся, если прямоугольники перекрываются. Граф перекрытий раскрашивается в минимальное число цветов. В результате: цвет – слой.

Если расслоение проводится после трассировки, то получают совмещенную топологию. Строят граф пересечений, в котором вершины – проводники, а ребра их соединяют, если проводники пересекаются. Граф пересечений раскрашивается в минимальное число цветов.

Расслоение в процессе трассировки будет рассмотрено в подразделе 7.4.7.

Алгоритмы раскраски графа

Задача раскраски вершин графа относится к NP-полным задачам. Различают точные и приближенные алгоритмы раскраски.

Примером точных алгоритмов служит алгоритм Вейссмана (J. Weissman). Иногда его называют алгоритмом, использующим метод Магу (K. Maghout).

Алгоритм Вейссмана

Алгоритм состоит из двух частей:

1. Построение семейства максимальных внутренне устойчивых множеств (МВУМ) (метод Магу);

2. Выбор минимального числа МВУМ, покрывающих все вершины графа (метод Петрика). Метод Петрика использовался в курсовой работе по дисциплине «Дискретная математика» для нахождения минимальных нормальных форм.

Идея метода Магу заключается в последовательном удалении из графа звездного подграфа с вершиной x_i.

Используется преобразование булевых выражений

(x_i Ú x₁) (x_i Ú x₂)...(x_i Ú x_j) = x_i Ú x₁ x₂...x_j.

Алгоритм состоит из следующих операций:

1. В матрице соединений R для каждой вершины подсчитывается число ненулевых элементов r_i;

2. Находится вершина x_i с max r_i, если таких вершин несколько, то выбирается любая;

3. Для выбранной вершины x_i записывается выражение

C_i = (x_i Ú x_a x_b...x_q), где Гx_i = {x_a, x_b, ..., x_q};

4. Из матрицы R удаляются строка и столбец, соответствующие вершине x_i;

5. Если R ¹ Æ, то переход к п. 2, иначе к п. 6;

6. Составляется конъюнкция П = Ù C_i. Раскрываются скобки. В полученной дизъюнкции на основе законов булевой алгебры выполняется минимизация. Т. к. в выражении нет отрицаний, используются только два закона: тавтологии аа=а ипоглощения a Ú ab = a;

7. Результат минимизации записывается в виде П = Ú K_j;

8. Для каждого K_j ищутся вершины графа, не вошедшие в него. Получено j_j и семейство МВУМ Y = {j₁, j₂, ..., j_l};

9. Для каждой вершины x_iÎ Х определяются подмножества j_j, в которые входит вершина x_iÎ j_j. Составляется дизъюнкция t_i = Ú j_j;

10. Составляется конъюнкция П’ = Ù t_i. Раскрываются скобки. В полученной дизъюнкции на основе законов булевой алгебры выполняется минимизация;

11. Получена дизъюнкция конъюнктивных термов П’ = Ú (Ù j_j). Выбирается конъюнктивный терм Ù j_j с минимальным числом сомножителей.

Количество сомножителей в этом терме и есть хроматическое число графа. Число минимальных термов – число вариантов раскраски графа. А каждое j_j – множество вершин, которые можно окрасить в один цвет.

Заметим, что п.п. 1-8 составляют метод Магу, а п.п. 9-11 – метод Петрика.

Пример. Раскрасить вершины графа рис.7.19.

x₅

x₁

x₆

x₃

x₄

x₂

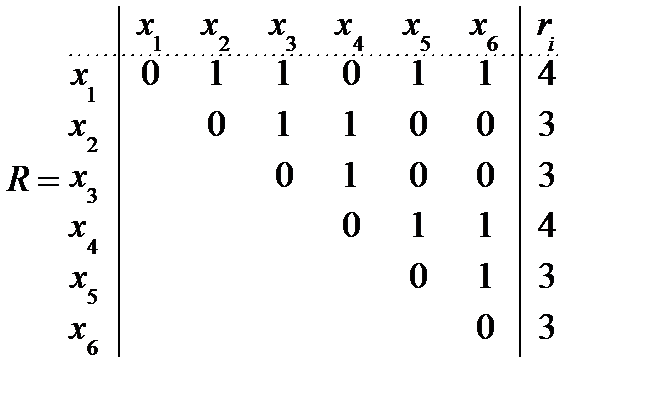
Рисунок 7.19. Исходный граф и его матрица соединений

1. В матрице R подсчитываем число ненулевых элементов r_i;

2. max r_i = r₁= r₄= 4, выбираем x₁;

3. Гx₁ = {x₂, x₃, x₅, x₆}, записываем выражение

C₁ = (x₁ Ú x₂ x₃ x₅ x₆);

4. Из матрицы R удаляем строку и столбец, соответствующие вершине x₁;

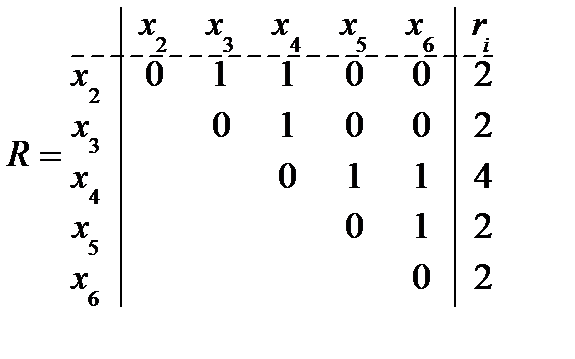
5. R ¹ Æ, max r_i = r₄= 4;

Гx₄ = {x₂, x₃, x₅, x₆}, C₄ = (x₄ Ú x₂ x₃ x₅ x₆);

6. Из матрицы R удаляем строку и столбец, соответствующие вершине x₄;

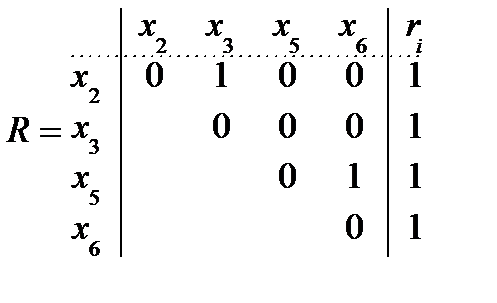
7. R ¹ Æ, max r_i = r₂= r₃= r₅= r₆= 1, выбираем x₂;

Гx₂ = {x₃}, C₂ = (x₂ Ú x₃);

8. Из матрицы R удаляем строку и столбец, соответствующие вершине x₂;

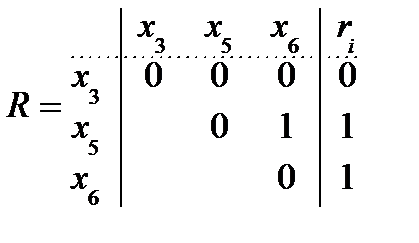
9. R ¹ Æ, max r_i = r₅= r₆= 1, выбираем x₅;

Гx₅ = {x₉}, C₅ = (x₅ Ú x₆);

10. Из матрицы R удаляем строку и столбец, соответствующие вершине x₅;

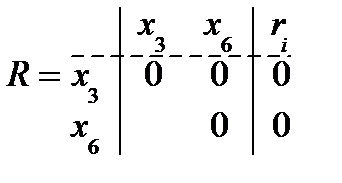
11. R =Æ;

12. Составляем конъюнкцию C_i и выполняем минимизацию

П = Ù C_i = C₁ C₂ C₄ C₅ = (x₁ Ú x₂ x₃ x₅ x₆)(x₂ Ú x₃)(x₄ Ú x₂ x₃ x₅ x₆)(x₅ Ú x₆) =

= x₁ x₂ x₄ x₅Ú x₁ x₂ x₄ x₆Ú x₁ x₃ x₄ x₅ Ú x₁ x₃ x₄ x₆ Ú x₂ x₃ x₅ x₆ = Ú K_j =

= K₁Ú K₂ Ú K₃ Ú K₄ Ú K₅;

13. Для каждого K_j ищем j_j:

j₁ = {x₃, x₆}, j₂ = {x₃, x₅}, j₃ = {x₂, x₆}, j₄ = {x₂, x₅}, j₅ = {x₁, x₄}. Получено семейство МВУМ Y ;

14. Для каждой вершины определим подмножества j_j, в которые она входит. Строим дизъюнкцию t_i = Ú j_j;

t₁= j₅; t₂ = j₃Ú j₄; t₃ = j₁Ú j₂; t₄ = j₅; t₅ = j₂Ú j₄; t₆ = j₁Ú j₃;

15. Составляем конъюнкцию и выполняем минимизацию булевой функции

П’ = Ù t_i = t₁ t₂ t₃ t₄ t₅ t₆ = j₅(j₃Ú j₄)(j₁Ú j₂) j₅(j₂Ú j₄)(j₁Ú j₃) = j₁j₄j₅ Ú j₂j₃j₅.

Хроматическое число графа c(G) = 3. Существует два варианта раскраски графа.

Первый: в синий цвет вершины j_{1 =}{x₃, x₆}, в зеленый - j₄ = {x₂, x₅}, в красный - j₅ = {x₁, x₄}.

Второй: в синий цвет вершины j_{2 =}{x₃, x₅}, в зеленый - j_{3 =}{x₂, x₆}, в красный - j₅ = {x₁, x₄}.

Недостататком точных алгоритмов является низкое быстродействие. Поэтому на практике используют приближенные алгоритмы, примером которых может служить алгоритм, использующий упорядочивание вершин.

⇐ Предыдущая 6 7 8 9 101112 13 14 15 Следующая ⇒