Осциллографа коэффициента передачи по напряжению

По определению коэффициент передачи по напряжению определяется из соотношения

(7)

где амплитуды гармонических сигналов на выходе и входе исследуемой цепи.

1. Осуществить выбор варианта из табл. 2.

Таблица 2

Исходные данные

Номер варианта (Задание 3, 4)	Форма сигнала	Значение сопротивления R1	Значение емкости С1	Частота сигнала	Амплитуда сигнала
		2 кОм	10 нФ	2 кГц	1 В
		10 кОм	400 нФ	3 кГц	3.2 В
		3 кОм	100 нФ	1 кГц	500 мВ
		8 кОм	1 мкФ	7 кГц	750 мВ
		900 Ом	4000 нФ	600 Гц	7 В
		15 кОм	1000 нФ	750 Гц	3.3 В

Окончание табл. 2

Номер варианта (Задание 3, 4)	Форма сигнала	Значение сопротивления R1	Значение емкости С1	Частота сигнала	Амплитуда сигнала
		2 кОм	50 нФ	2 кГц	2 В
		2400 Ом	900 нФ	3400 Гц	2.2 В
		23 кОм	150 нФ	6300 Гц	4.7 В
		12 кОм	2 мкФ	8 кГц	5000 мкВ
		1.5 кОм	300 нФ	10 кГц	2.5 В
		2 кОм	500 нФ	9 кГц	12 В
		15 кОм	10 нФ	855 Гц	100 мВ
		5 кОм	200 нФ	5600 Гц	12.5 В
		3 кОм	1500 нФ	12.5 кГц	5.5 В
		200 Ом	500 нФ	9.5 кГц	130 мкВ
		15 кОм	3 мкФ	4.7 кГц	27000 мкВ
		50 кОм	15 нФ	3.8 кГц	3.4 В
		1300 Ом	1 мкФ	15 кГц	700 мВ
		12 кОм	100 нФ	860 Гц	2.1 В
		1100 Ом	2 мкФ	458 Гц	5.7 В
		800 Ом	0.5 мкФ	760 Гц	2.7 В
		9 кОм	700 нФ	5.8 кГц	130 мВ
		2 кОм	850 нФ	2.1 кГц	1500 мВ
		7 кОм	0.5 мкФ	3700 Гц	4 В
		600 Ом	0.7 мкФ	6700 Гц	6 В
		1 кОм	1 мкФ	730 Гц	15 В
		40 кОм	30 нФ	2.2 кГц	24 В
		3000 Ом	730 нФ	645 Гц	230 мкВ
		20000 Ом	540 нФ	730 Гц	24000 мкВ
		1000 Ом	1.5 мкФ	1300 Гц	150 мкВ
		10000 Ом	0.6 мкФ	4000 Гц	3 В

2. Собрать схему, приведенную на рис. 5. Установить параметры элементов схемы в соответствии с вариантом. На выходе генератора установить гармонические колебания с заданной амплитудой и частотой .

Рис. 5. Схема измерения коэффициента передачи и фазового сдвига

3. На экране осциллографа получить устойчивое не искаженное изображение входного и выходного сигналов и измерить их амплитуды , .

4. По экспериментальным данным рассчитать коэффициент передачи .

5. Анализ RC-цепи показывает, что ее коэффициент передачи определяется выражением

(8)

где сопротивление резистора R1 RC-цепи, Ом;

значение емкости конденсатора C1 RC-цепи, Ф;

циклическая частота гармонического сигнала, , Гц.

Рассчитать по приведенной формуле коэффициент передачи и сравнить его со значением, полученным экспериментально.

Задание 4. Измерение с помощью двухканального

Осциллографа фазового сдвига двух гармонических сигналов

В простейших RC (RL)–цепях

1. Собрать схему, приведенную на рис. 5. Установить параметры элементов схемы в соответствии с вариантом (см. табл. 2).

2. На выходе генератора установить гармонические колебания с заданной амплитудой и частотой.

3. На экране осциллографа получить устойчивое не искаженное изображение обоих сигналов и определить их фазовый сдвиг .

Фазовый сдвиг можно определить с помощью следующей формулы:

(9)

где период сигнала (рис. 6);

начальные фазы входного и выходного сигналов;

временной сдвиг между сигналами (рис. 7).

Рис. 6. Измерение периода сигнала

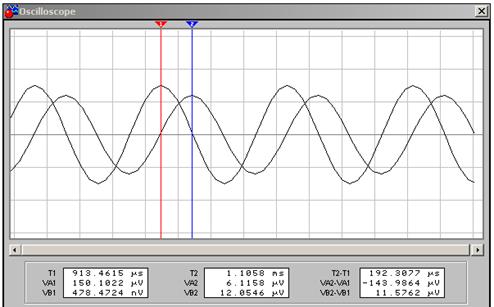
Временной сдвиг на экране осциллографа можно измерить, используя визирные линии, которые ориентируют по максимуму гармонической функции, как показано на рис. 7. Величину временного сдвига можно прочесть в окне под экраном (см. рис. 7).

Рис. 7. Измерение временного сдвига двух гармонических сигналов

Для случая, приведенного на рис. 6-7, величина фазового сдвига двух гармонических сигналов составит

4. Результаты измерений и расчетов занести в отчет.

Следует отметить, что выходной сигнал может отставать по фазе от входного сигнала и тогда он располагается справа от входного (см. рис. 7). Фазовый сдвиг в этом случае берется со знаком минус. В случае опережения выходного сигнала (он располагается слева от входного) фазовый сдвиг берется положительным. На рис. 7 . Выходной сигнал отстает по фазе от входного на .

Задание 5. Измерение частотных характеристик

Простейших RC (RL)–цепей с помощью измерителя

Диаграмм Боде

Частотными характеристиками цепи называют функции, характеризующие реакцию цепи на синусоидальное входное воздействие в установившемся режиме. Данные характеристики имеют очень большое значение при анализе работы цепи. Кратко охарактеризуем каждую из характеристик.

Если на вход цепи подается величина (рис. 8)

то на выходе в установившемся режиме получаем

где – амплитуда;

– фаза сигнала;

циклическая частота.

Рис. 8. Структурная схема исследуемой электрической цепи

Каждой гармонической функции времени можно поставить в соответствие комплексное число, называемое мгновенным комплексом гармонической функции (рис. 9):

Рис. 9. Мгновенный комплекс гармонической функции

Функцию называют амплитудно-фазовой частотной характеристикой цепи (АФЧХ). Функция называется соответственно амплитудно-частотной характеристикой цепи (АЧХ), – фазовой частотной характеристикой цепи (ФЧХ).

Функцию можно представить в виде

где и – соответственно вещественная и мнимая частотные характеристики. Исходя из этого, функции АЧХ и ФЧХ можно представить как:

Кроме частотных характеристик используются логарифмические частотные характеристики – логарифмическая амплитудно-частотная (ЛАЧХ) и логарифмическая фазовая частотная (ЛФЧХ) характеристики.

ЛАЧХ – это зависимость от логарифма частоты . При построении ЛАЧХ по оси абсцисс откладывают частоту в логарифмическом масштабе, а по оси ординат .

ЛФЧХ – это зависимость фазовой частотной функции от логарифма частоты . При ее построении по оси абсцисс откладывают частоту в логарифмическом масштабе, по оси ординат откладывают в градусах или радианах.

За единицу масштаба по оси абсцисс принимается декада – частотный интервал, соответствующий изменению частоты в 10 раз. Ось ординат при построении этих характеристик проводят через произвольную, удобную для рассматриваемой задачи, точку, а не через точку w=0, поскольку частоте w=0 соответствует бесконечно удаленная точка.

Единицей является децибел (дБ), равный одной десятой Бела. Бел – это единица десятичного логарифма коэффициента усиления мощности сигнала, т. е. 1 Бел соответствует усилению мощности в 10 раз. Поскольку мощность сигнала пропорциональна квадрату амплитуды, а , то усиление в Белах, выраженное через отношение амплитуд, равно . дБ означает, что на данной частоте при прохождении сигнала через цепь его амплитуда увеличивается в 10 раз.

ЛАЧХ и ЛФЧХ за счет использования логарифмических шкал более удобны при анализе работы цепи в широком диапазоне изменения частоты сигнала.

Измеритель диаграмм Боде предназначен для измерения АЧХ, ФЧХ, ЛАЧХ и ЛФЧХ электрических цепей.

1. Собрать схему, приведенную на рис. 10. Установить параметры элементов схемы в соответствии с вариантом (см. табл. 2).

Рис. 10. Схема измерения частотных характеристик цепи

2. На выходе генератора установить гармонические колебания с заданной амплитудой и частотой.

3. На экране измерителя диаграмм Боде получить устойчивое изображение ЛАЧХ или АЧХ цепи (рис. 11). С помощью визирной линии снять несколько значений ЛАЧХ (или АЧХ) и зарисовать ее в отчете. Сделать выводы.

RC-цепь, представленная на рис. 10, представляет собой пассивный фильтр низких частот. Конденсатор С1 для сигнала низкой частоты (ниже частоты среза) является большим сопротивлением, и сигнал поступает на выход фильтра. Для сигнала высокой частоты (выше частоты среза) конденсатор является хорошим проводником, и поэтому он шунтирует данный сигнал, не пропуская его на выход. Частотой среза называется частота, при которой напряжение на выходе фильтра падает до уровня 0, 707 от напряжения в полосе пропускания (т. е. падает на 3 дБ). Для случая, представленного на рис. 11, частота среза фильтра составляет приблизительно Гц, т. е. выше данной частоты амплитуда сигнала на выходе фильтра, как видно из ЛАЧХ, все более ослабевает.

4. Определить частоту среза фильтра.

Рис. 11. ЛАЧХ цепи и значение частоты среза фильтра

5. Нажатием кнопки Phase на панели управления измерителя, а также кнопками настройки прибора получить устойчивое изображение ЛФЧХ или ФЧХ цепи (рис. 12). С помощью визирной линии снять несколько значений ЛФЧХ (или ФЧХ) и зарисовать ее в отчете. Сделать выводы.

Рис. 12. ЛФЧХ цепи

Лабораторная работа № 2

⇐ Предыдущая 123 4 Следующая ⇒