Введение фиктивного поставщика (потребителя) для сведения данной транспортной модели к ЗТЗ.

Любую открытую модель можно преобразовать в закрытую.

Если общие запасы превышают потребности ( ), то в модель вводят еще одного потребителя, (m+1)-го по счету. Его принято называть дополнительным или фиктивным. На самом деле его нет, но условно можно считать, что именно к нему свозят все излишки. Соответственно, его «потребность» в продукции b_m+1 примем равной . Одновременно в модель вводятся n новых переменных x_im+1, . Каждая из этих переменных по экономическому смыслу представляет собой излишек продукции у i-го поставщика (столько продукции «везут» от i-го поставщика фиктивному потребителю). При этом все новые переменные в целевую функцию не входят (т.е. входят с нулевыми коэффициентами
c_im+1 = 0), поскольку на самом деле перевозки этой продукции не осуществляются. Излишек продукции остается у поставщиков, следовательно, и платить за его перевозку не надо.

Тогда транспортная задача примет вид:

(1)

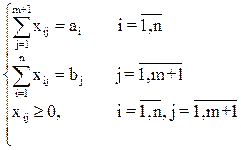
При этом целевая функция в модели (6) может также иметь вид (отброшенные слагаемые все равно нулевые).

Собственно, в зависимости от экономической интерпретации открытой модели критерий ее разрешимости можно и вообще снять. А именно, если общий объем потребностей превышает объем запасов ( ), можно аналогично ввести дополнительного (фиктивного) поставщика, (n+1)-го по счету. Условно будем считать, что именно у этого поставщика находится вся недостающая продукция, поэтому его запасы а_n+1 = . При этом также придется ввести m новых переменных x_n+1j, - это дефицит продукции у j-го потребителя (т.е. та продукция, которую ему «везут» от несуществующего поставщика; этому потребителю ее не хватит). Разумеется, за перевозки несуществующей продукции не платят, поэтому все c_n+1j = 0.

Тогда модель примет вид:

или

(2)

Итак, если в транспортной модели допускается дефицит, то она всегда будет разрешима после преобразования открытой модели в закрытую.

Модель ТЗ (закрытая или открытая) может применяться не только для транспортировки грузов, но и в других задачах распределения ресурсов: распределение удобрений по участкам с различным плодородием для получения наибольшего урожая, распределения сельскохозяйственных культур по пашням для получения максимального дохода от реализации, распределение марок тракторов и подвесных орудий по видам механизированных работ для выполнения этих работ с минимальными затратами и т.д. При этом сама формулировка ТЗ может быть усложнена особыми требованиями: минимизация суммарных затрат на производство продукции и ее транспортировку ( в этом случае тариф – сумма затрат на производство и транспортировку), запрет отдельных поставок ( в этом случае соответствующая клетка распределительной таблицы блокируется завышенным тарифом) и др.

 

2. Методическое обеспечение

2.1. Методические указания по выполнению практических илабораторных работ для студентов технологического факультета по направлению подготовки 23.05.01 - Наземные транспортно-технологические средства

Помимо лекций студент должен систематически и полно готовиться к каждому практическому занятию. Предварительно требуется изучить материал соответствующих лекций и прочитать учебник. Необходимо запомнить формулировки теорем и необходимые определения математических понятий. Требуется подробно разобрать типовые примеры, решенные в лекциях и учебнике. Желательно, закрыв книгу и тетрадь, самостоятельно решить те же самые примеры. Затем следует выполнить все домашние и незаконченные аудиторные задания. Задачи должны решаться с пояснениями и ссылками на соответствующие формулы и теоремы. Формулы следует выписывать с объяснениями соответствующих буквенных обозначений величин, входящих в них. Практические занятия проводятся с целью углубленного освоения материала лекции, выработки навыков в решении практических задач и производстве расчетов. Главным содержанием практических занятий является активная работа каждого студента.

Для достижения указанной цели решаются следующие задачи:

− формирование знаний методов и алгоритмов эффективного решения задач дискретной оптимизации;

− формирование умений и навыков использования изученных методов для решения типовых задач математического моделирования и оценки пределов применимости полученных результатов.

 

МОДУЛЬ 1. АЛГЕБРА СОБЫТИЙ

 

Практическое занятие № 1

 

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться: